Syntaxe.
QUARTILE (matrice; quart)
Définition.
Cette fonction renvoie le quartile d’un ensemble de données. Les quartiles sont souvent utilisés dans les données des ventes et des enquêtes pour diviser les populations en groupes. Par exemple, vous pouvez utiliser QUARTILE () pour rechercher les 25% de revenus les plus élevés d’une population.
L’argument quart indique quelle valeur renvoyer. Le tableau 12-3 répertorie les valeurs de cet argument.
Arguments
■ matrice (obligatoire). Le tableau ou la plage de cellules de valeurs numériques pour lesquelles vous voulez la valeur quartile
■ quart (requis). Indique quelle valeur renvoyer
REMARQUE
Si array est vide, QUARTILE () renvoie le #NUM! valeur d’erreur. Si quart n’est pas un entier, les décimales sont tronquées. Si quart est inférieur à 0 ou supérieur à 4, la fonction QUARTILE () renvoie le #NUM! Erreur.
MIN (), MEDIAN () ou MAX () renvoient la même valeur que QUARTILE () si le quartile est 0, 2 ou 4, respectivement.
Contexte.
En utilisant des quantiles et des quartiles, vous pouvez calculer la distribution des données. Alors que la médiane divise la distribution en deux, le quantile divise la distribution en plusieurs parties égales, et le quartile divise la distribution en quatre parties égales.
La fonction QUARTILE () requiert l’argument de tableau indiquant la plage à évaluer et l’argument de quart indiquant le quartile à renvoyer. Cela peut être n’importe quelle valeur de 0 à 4.
Le tableau 12-3 répertorie les valeurs de l’argument quart.
Les valeurs pour le quart argument
Valeur Résultat
0 Plus petite valeur (minimum)
1 quartile inférieur (quantile de 25%)
2 médiane (quantile à 50%)
3 quartile supérieur (quantile à 75%)
4 plus grande valeur (maximum)
Si le quartile 0 est le minimum, le quartile 4 le maximum et le deuxième quartile la médiane, les quartiles 1 et 3 peuvent être facilement calculés.
Exemple.
Une entreprise pharmaceutique qui fabrique des pilules contre les maux de tête et les vend dans l’ensemble du pays veut évaluer les ventes de pilules dans les différentes régions numérotées de 1 à 5 (Texas, Virginie, Californie, Oregon et Washington) pour chaque tranche de 100 000 habitants dans chaque État. L’objectif est de calculer quelle part des ventes représente 25% des ventes d’un État en un an (voir la figure). Vous connaissez les ventes pour un an (12 valeurs) par État. Pour calculer le quartile, vous devez trier les valeurs par ordre croissant.
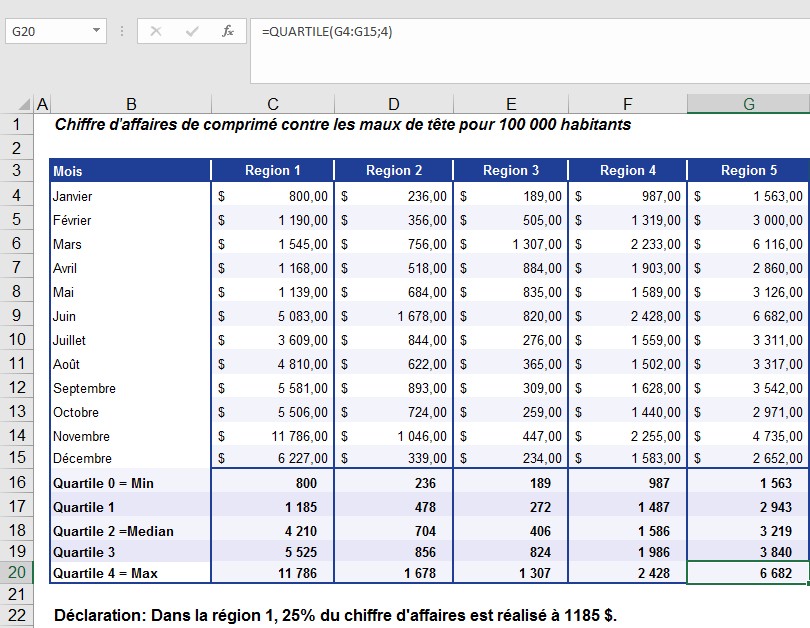
Figure . Pour un meilleur aperçu, les ventes annuelles dans les États sont divisées en quartiles.
Les ventes pour la région 1 indiquent que la plus petite valeur est le minimum, la plus grande valeur est le maximum et le deuxième quartile (50% et la médiane) est de 4 210.
Comment pouvez-vous calculer le deuxième quartile sans utiliser la fonction QUARTILE ()? Le nombre de valeurs étant pair, la limite de 50 doit être comprise entre la cinquième et la sixième valeur. Si vous ajoutez les deux valeurs et divisez le résultat par 2, vous obtenez la médiane. S’il y avait 13 valeurs, la médiane ou le deuxième quartile serait la septième valeur.
Vous avez déjà les quartiles suivants:
Quartile 0 = 800
Quartile 2 = 4 210
Quartile 4 = 11 786
Maintenant, vous avez toujours besoin des quartiles 1 et 3 (les centiles limite de 25% et 75%). Donc vous
trouver les valeurs aux positions 0.25 et 0.75 sur la base des données originales. Vous devez calculer les valeurs pour lesquelles 25% des observations sont inférieures ou égales à la valeur (le premier quartile) et 75% des observations sont supérieures ou égales à celle-ci (le troisième quartile).
Vous avez 12 valeurs numériques (n). Si vous multipliez n par 0,25 et 0,75, vous découvrez que le premier quartile se situe entre les troisième et quatrième valeurs et que le troisième quartile se situe entre les neuvième et dixième valeurs des données d’origine triées.
La fonction QUARTIL () renvoie les résultats suivants pour le premier et le troisième quartile:
Quartile 1 = 1 185 Quartile 3 = 5 525
Le premier quartile se situe entre les troisième et quatrième valeurs mais pas au milieu et davantage vers la quatrième valeur.
Vous pouvez maintenant tirer les conclusions suivantes:
■ Dans la région 1, 25% des ventes atteignent 1 185,00 USD.
■ Dans la région 5, 75% des ventes atteignent 3 840,00 USD.
