Syntaxe.

LOI.LOGNORMALE.INVERSE (probabilité, moyenne, ecart_type)

Définition.

Cette fonction renvoie le quantile de la distribution log-normale de x, où ln (x) est normalement distribué avec les paramètres moyenne et ecart_type. Ifp = LOGNORM.DIST (x, …) alors

LOGNORN. INV (p, …) = x. Si la probabilité est p, vous pouvez calculer le quantile de la distribution log-normale.

Utilisez la distribution log-normale pour analyser des données transformées de façon logarithmique.

Arguments

■ probabilité (obligatoire). Une probabilité associée à la distribution log-normale

■ moyenne (obligatoire). La moyenne de la distribution log-normale

■ ecart_type (obligatoire). L’écart-type de la distribution log-normale

REMARQUE

Si l’un des arguments n’est pas une expression numérique, la fonction LOI.LOGNORMALE.INVERSE () renvoie le #VALUE! Erreur.

Si la probabilité est inférieure à 0 ou supérieure à 1, la fonction LOI.LOGNORMALE.INVERSE () renvoie le #NUM! Erreur.

Si ecart_type est inférieur ou égal à 0, la fonction renvoie le #NUM! Erreur.

Contexte.

L’inverse de la fonction de distribution log-normale est:

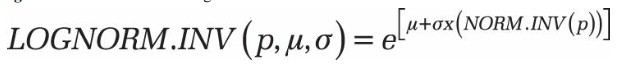
Exemple.

Utilisez les valeurs suivantes pour calculer LOI.LOGNORMALE.INVERSE ():

■ 0,039084 = la probabilité associée à la distribution log-normale (probabilité)

■ 3,5 = la moyenne de ln (x) (moyenne)

■ 1,2 = l’écart type de ln (x) (ecart_type)

La figure illustre le calcul de LOI.LOGNORMALE.INVERSE ().

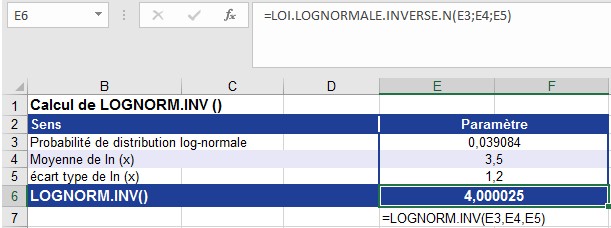
Figure Calcul de LOGNORM.DIST ().
La fonction LOGNORM.DIST () renvoie la distribution lognormale cumulative de 0,039084 en fonction des paramètres illustrés à la figure.