Syntaxe.
INTERVALLE.CONFIANCE.STUDENT (alpha; écart_type; taille)
Définition.
Cette fonction renvoie l’intervalle de confiance de la valeur attendue d’une variable aléatoire à l’aide du test t de Student.
Arguments
■ alpha (obligatoire). La probabilité d’erreur utilisée pour calculer l’intervalle de confiance. L’intervalle de confiance est égal à 100*(1 – alpha)%, ce qui signifie qu’un alpha de 0,05 indique un niveau de confiance de 95%.
■ écart_type (obligatoire). L’écart type de la population. L’argument standard_dev est supposé connu.
■ taille (obligatoire). La taille de l’échantillon.
REMARQUE
Si l’un des arguments n’est pas une valeur numérique, la fonction INTERVALLE.CONFIANCE.STUDENT() renvoie le #VALUE! Erreur.
Si alpha est inférieur ou égal à 0 ou supérieur ou égal à 1, INTERVALLE.CONFIANCE.STUDENT() renvoie le #NUM! Erreur.
Si standarddev est inférieur ou égal à 0, la fonction renvoie le #NUM! Erreur.
Si la taille n’est pas un entier, les décimales sont tronquées. Si la taille est inférieure à 1, la fonction renvoie le #NUM! Erreur.
Si alpha est égal à 0,05, vous devez calculer l’aire sous la distribution normale standard égale à (1-alpha) ou à 95%. Cette valeur est ± 1,96. Par conséquent, l’intervalle de confiance est:
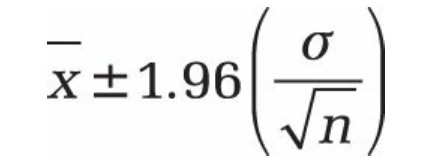
Contexte.
En statistique, les intervalles de confiance sont une méthode couramment utilisée pour indiquer la précision des valeurs estimées. Plus l’intervalle de confiance est élevé, moins les informations sont précises. Un intervalle de confiance inférieur est plus susceptible de renvoyer la valeur exacte.
Pour cette raison, l’écart type de la variance ou de l’intervalle de confiance est généralement spécifié en plus de la moyenne calculée.
La fonction INTERVALLE.CONFIANCE.STUDENT() détermine l’intervalle de confiance 1 alpha pour la valeur attendue (moyenne) d’une distribution de probabilité. alpha est la probabilité d’erreur ou le risque alpha. Seules les valeurs comprises dans l’intervalle [0..1] sont valides (0 à 100%). Si alpha vaut 0,05 (5%), la probabilité que la moyenne se situe en dehors de l’intervalle calculé par INTERVALLE.CONFIANCE.STUDENT() est de 5%.
En d’autres termes, la probabilité que la moyenne de la population se situe dans l’intervalle calculé est de 95%. C’est ce qu’on appelle un intervalle de confiance de 95%.
Un échantillon d’une population distribuée normale avec un écart-type et une moyenne connus est utilisé pour calculer l’intervalle de confiance. La fonction INTERVALLE.CONFIANCE.STUDENT() renvoie la moitié de l’intervalle de confiance de la moyenne arithmétique de l’échantillon. Cela signifie que l’intervalle de confiance 1 alpha est une zone symétrique autour de la moyenne d’un échantillon contenant la moyenne de la population avec une probabilité de 1 alpha.
Exemple. Nous allons utiliser l’exemple de l’éditeur de logiciel pour expliquer INTERVALLE.CONFIANCE.STUDENT(). La société vend tous ses produits via son site Web interne. Vous êtes le responsable marketing et souhaitez analyser plus en détail les chiffres des quatre dernières années. Vous avez entré le nombre de visites sur le site Web et de commandes en ligne par mois dans Excel (voir la figure ).
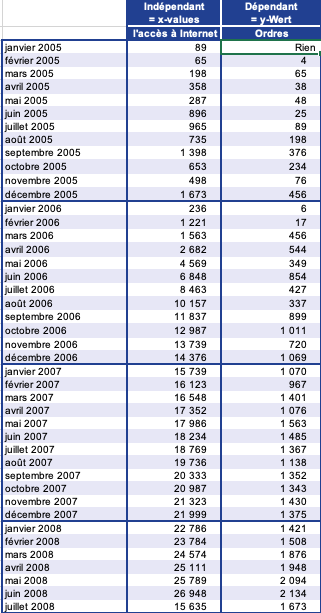
Le nombre de visites de sites Web et de commandes en ligne.
Vous avez également déjà calculé la moyenne d’échantillon et la déviation standard de la population pour les deux zones. Comme vous utilisez un seul échantillon, vous calculez un intervalle de confiance de 95% pour la moyenne de la population (voir la figure ).

Figure . Calcul de la moyenne, de la déviation standard et de la taille de l’échantillon.
Parce que vous voulez un niveau de confiance de 95%, alpha = 0,05 (5%).
La figure montre le calcul de l’intervalle de confiance pour la moyenne des visites sur le site Web et la moyenne des commandes en ligne.
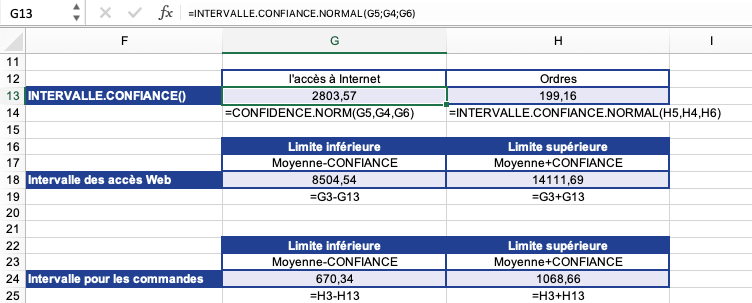
Figure . INTERVALLE.CONFIANCE.NORMAL() calcule l’intervalle de confiance 1 alpha.
Pour les visites de sites Web, la fonction INTERVALLE.CONFIANCE.NORMAL() renvoie 2803,57 (la moitié de l’intervalle de confiance de la moyenne arithmétique de l’échantillon).
Pour déterminer les limites inférieure et supérieure de l’intervalle, la moyenne de l’échantillon plus INTERVALLE.CONFIANCE.NORMAL() ainsi que la moyenne de l’échantillon moins INTERVALLE.CONFIANCE.NORMAL() ont été calculées.
Le résultat pour la limite inférieure est 8504,54 et le résultat pour la limite supérieure est 14 111,69.
Déclarations Vous vous attendiez à une valeur alpha de 0,05 et tirez les conclusions suivantes en fonction du résultat:
■ La moyenne de la population pour les visites sur le site Web se situe entre 8504,54 et 14 111,69 avec un intervalle de confiance de 95%.
■ Étant donné que la taille de l’échantillon n’est que de 43, l’intervalle de confiance est imprécis. Plus l’échantillon est grand, plus l’intervalle de confiance est précis-et la moyenne de la population est également plus précise.
