Qu’est-ce que la variable aléatoire de Poisson?

■■ Comment puis-je calculer les probabilités pour la variable aléatoire de Poisson?

■■ Si le nombre de clients arrivant dans une banque est régi par une variable aléatoire de Poisson, quelle variable aléatoire régit le temps entre les arrivées?

Réponses aux questions de cet article

Cette section fournit les réponses aux questions répertoriées au début de cet article.

Qu’est-ce que la variable aléatoire de Poisson?

La variable aléatoire de Poisson est une variable aléatoire discrète qui est utile pour décrire les probabilités pour les situations dans lesquelles les événements (tels que les arrivées de clients dans une banque ou les commandes passées pour un produit) ont une faible probabilité de se produire pendant un court intervalle de temps. Plus précisément, pendant un court intervalle de temps, noté t, zéro ou un événement se produira, et la probabilité qu’un événement se produise pendant un court intervalle de longueur t est (pour certains λ) donnée par λt. Ici, λ est le nombre moyen d’occurrences par unité de temps.

Les situations dans lesquelles la variable aléatoire de Poisson peut être appliquée sont les suivantes:

■■ Nombre d’unités d’un produit demandées pendant un mois.

■■ Nombre de morts par an à coups de pied dans l’armée prussienne.

■■ Nombre d’accidents de voiture que vous avez au cours d’une année.

■■ Nombre d’exemplaires de The Seat of the Soul commandés aujourd’hui sur Amazon.com.

■■ Nombre de demandes d’indemnisation des accidents du travail déposées dans une entreprise ce mois-ci.

■■ Nombre de défauts dans 100 mètres de corde. (Ici, 1 mètre de ficelle joue le rôle du temps.)

Comment puis-je calculer les probabilités pour la variable aléatoire de Poisson?

Vous pouvez utiliser la fonction LOI.POISSON.N de Microsoft Excel  pour calculer les probabilités impliquant la variable aléatoire de Poisson. Dans les versions antérieures d’Excel, la fonction POISSON générait des probabilités POISSON. N’oubliez pas que dans un laps de temps t, la moyenne d’une variable aléatoire de Poisson est t. La syntaxe de la fonction POISSON est la suivante:

LOI.POISSON.N (x, Lambda, Vrai_ou_1) calcule la probabilité qu’une variable aléatoire de Poisson avec une moyenne égale à Lambda soit inférieure ou égale à x.

LOI.POISSON.N (x, Lambda, Faux_ou_0) calcule la probabilité qu’une variable aléatoire de Poisson avec une moyenne égale à Lambda soit égale à x.

Voici quelques exemples de calcul des probabilités pour les variables aléatoires de Poisson. Vous pouvez recherchez ces exemples dans le fichier , illustré à la figure 1.

FIGURE 1 Utilisation de la variable aléatoire de Poisson.

Supposons que mon entreprise de conseil reçoive en moyenne 30 appels téléphoniques par heure. Pendant une période de deux heures, je souhaite déterminer les éléments suivants:

■■ La probabilité de recevoir exactement 60 appels dans les deux prochaines heures

■■ La probabilité que le nombre d’appels reçus au cours des deux prochaines heures soit inférieur ou égal à 60

■■ La probabilité que de 50 à 100 appels soient reçus dans les deux prochaines heures

Au cours d’une période de deux heures, le nombre moyen d’appels est de 60. Dans la cellule C4, je trouve la probabilité (0,05) que exactement 60 appels seront reçus dans les deux prochaines heures en utilisant le LOI.POISSON.N (60, C2, False ) formule. Dans la cellule C5, je trouve la probabilité (0,534) qu’au plus 60 appels soient reçus en deux heures avec la formule LOI.POISSON.N (60, C2, VRAI). Dans la cellule C6, je trouve la probabilité (0,916) que de 50 à 100 appels seront reçus en deux heures avec le LOI.POISSON.N (100, C2, ) – LOI.POISSON.N (49, C2, Vrai) formule.

Remarque Vous pouvez toujours utiliser 1 au lieu de Vrai comme argument dans n’importe quelle fonction Excel.

Si le nombre de clients arrivant dans une banque est régi par une variable aléatoire de Poisson, quelle variable aléatoire régit le temps entre les arrivées?

Le temps entre les arrivées peut avoir n’importe quelle valeur, ce qui signifie que le temps entre les arrivées est une variable aléatoire continue. Si une moyenne des arrivées se produit par unité de temps, le temps entre les arrivées suit une variable aléatoire exponentielle ayant la fonction de densité de probabilité (pdf) de f (t) = λ – λt. Cette variable aléatoire a une valeur moyenne ou moyenne égale à 1 / λ. Pour λ = 30, un graphique du pdf exponentiel est illustré à la figure 2. Vous pouvez trouver ce graphique et les données de cet exemple dans la feuille de calcul Densité dans le fichier .

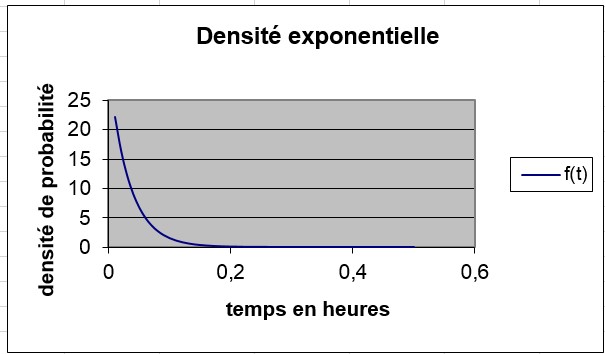
FIGURE 2 Fonction de densité de probabilité exponentielle.

Rappelons dans l’article 66, «Introduction aux variables aléatoires», que pour une variable aléatoire continue, la hauteur du pdf pour un nombre x reflète la probabilité que la variable aléatoire suppose

une valeur proche de x. Vous pouvez voir dans la figure 2 que des délais extrêmement courts entre les arrivées bancaires (par exemple, moins de 0,05 heure) sont très probables, mais que pour des délais plus longs, le pdf diminue fortement.

Même si le temps moyen entre les arrivées est de 1/30 = 0,033 heure, il y a une chance raisonnable que le temps entre les arrivées atteigne 0,20 heure.

 La formule LOI.EXPONENTIELLE.N (x, 1 / mean, VRAI_ou_1)  donnera la probabilité qu’une variable aléatoire exponentielle avec un g       Une moyenne donnée prendra une valeur inférieure ou égale à x. Ainsi, le deuxième argument de la fonction LOI.EXPONENTIELLE.N est le taux par unité de temps auquel les événements se produisent. Par exemple, pour calculer la probabilité que l’intervalle entre les arrivées soit d’au moins 5, 10 ou 15 minutes, vous pouvez copier la formule 1 – LOI.EXPONENTIELLE.N (C5, $ D $ 2, Vrai_ou_1) de la cellule D5 à D7. Dans les versions antérieures d’Excel, la fonction LOI.EXPONENTIELLE.N donne les mêmes résultats que LOI.EXPONENTIELLE.N.

Notez que les minutes ont d’abord été converties en heures (5 minutes correspondent à 1/12 heure, etc.). De plus, le temps moyen entre les arrivées est de 0,033 heure, donc 1 / Mean = 1 / .033 = 30 a été entré dans la formule. En bref, le taux d’arrivée par unité de temps a été saisi, comme vous pouvez le voir sur la figure 3.

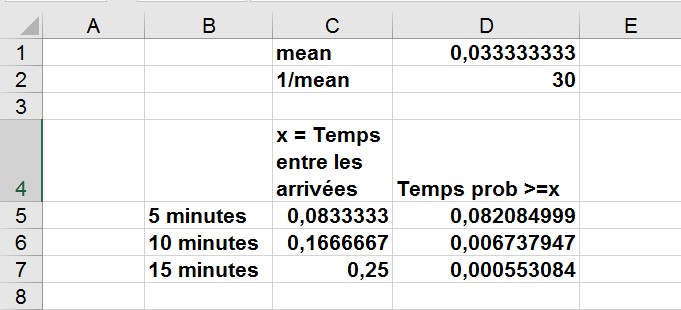
FIGURE 3 Calculs des probabilités exponentielles.