■■ Le propriétaire de mon entreprise, qui publie des livres informatiques, veut savoir si la position de nos livres dans la section des livres informatiques des librairies influence les ventes. Plus précisément, est-il vraiment important que les livres soient placés à l’avant, à l’arrière ou au milieu de la section des livres informatiques?

■■ Si je détermine si les populations ont des moyens significativement différents, pourquoi la technique s’appelle-t-elle analyse de la variance?

■■ Comment puis-je utiliser les résultats de l’ANOVA unidirectionnelle pour les prévisions?

Les analystes de données disposent souvent de données sur plusieurs groupes de personnes ou d’éléments et souhaitent déterminer

si les données sur les groupes diffèrent de manière significative. Voici quelques exemples:

■■ Y a-t-il une différence significative dans la durée pendant laquelle quatre médecins gardent les mères

l’hôpital après l’accouchement de ces patientes?

■■ Le rendement de production d’un nouveau médicament dépend-il si la taille du contenant dans lequel le médicament est produit est grande, petite ou moyenne?

■■ La baisse de la pression artérielle atteinte après la prise d’un des quatre médicaments dépend-elle du médicament pris?

Lorsque vous essayez de déterminer si les moyennes de plusieurs ensembles de données qui dépendent d’un facteur sont sensiblement différentes, l’analyse unidirectionnelle de la variance, ou ANOVA, est l’outil approprié à utiliser. Dans les exemples précédents, les facteurs sont respectivement les médecins, la taille du contenant et le médicament. En analysant les données, vous pouvez choisir entre deux hypothèses:

■■ Hypothèse nulle, qui indique que les moyennes de tous les groupes sont identiques.

■■ Hypothèse alternative, qui indique une différence statistiquement significative entre les veux dire que.

Le propriétaire de mon entreprise, qui publie des livres informatiques, veut savoir si la position de nos livres dans la section des livres informatiques des librairies influence les ventes. Plus précisément, est-il vraiment important que les livres soient placés à l’avant, à l’arrière ou au milieu de la section des livres informatiques?

La maison d’édition veut savoir si ses livres se vendent mieux lorsqu’un affichage est installé à l’avant, à l’arrière ou au milieu de la section des livres informatiques. Les ventes hebdomadaires (en centaines) ont été suivies à 12 magasins. Dans cinq magasins, les livres étaient placés à l’avant; dans quatre magasins, à l’arrière; et dans trois magasins, au milieu. Les ventes résultantes sont contenues dans la feuille de calcul Signifie dans le fichier , qui est illustré à la figure 1. Les données indiquent-elles que l’emplacement des livres a un effet significatif sur les ventes?

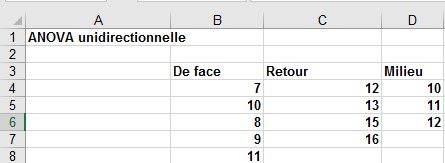
FIGURE 1 Données sur les ventes de livres.

Vous pouvez supposer que les 12 magasins ont des modèles de vente similaires et sont approximativement de la même taille. Cette hypothèse vous permet d’utiliser l’ANOVA unidirectionnelle car vous pensez qu’au plus un facteur (la position de l’affichage dans la section du livre d’ordinateur) affecte les ventes. (Si les magasins étaient de tailles différentes, vous auriez besoin d’analyser les données avec une ANOVA bidirectionnelle, qui est abordée au chapitre 61, «Blocs randomisés et ANOVA bidirectionnelle».)

Pour analyser les données, sous l’onglet Données, cliquez sur Analyse des données, puis sélectionnez Anova: facteur unique. Remplissez la boîte de dialogue comme illustré à la figure 2.

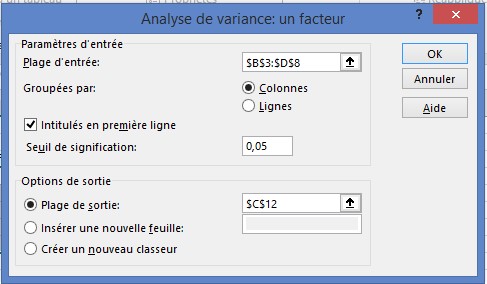
FIGURE 2 Anova: boîte de dialogue à facteur unique.

Utilisez les configurations suivantes:

■■ Les données de votre plage d’entrée, y compris les étiquettes, se trouvent dans les cellules B3: D8.

■■ Sélectionnez Étiquettes dans la première ligne car la première ligne de la plage d’entrée contient des étiquettes.

■■ Sélectionnez Colonnes car les données sont organisées en colonnes.

■■ Sélectionnez C12 comme cellule supérieure gauche de la plage de sortie.

■■ La valeur alpha sélectionnée n’est pas importante. Vous pouvez utiliser la valeur par défaut.

Après avoir cliqué sur OK, vous obtenez les résultats illustrés à la figure 3.

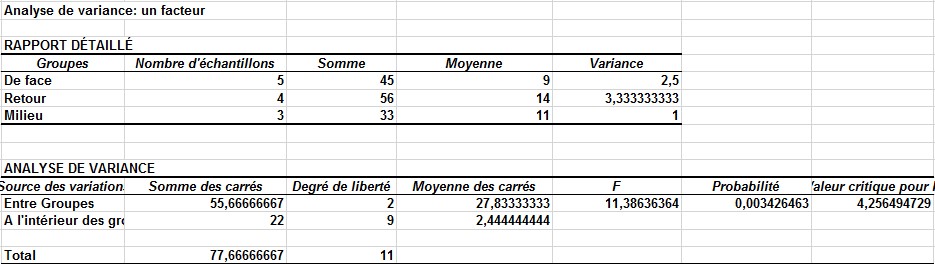
FIGURE 3 Résultats ANOVA unidirectionnels.

Dans les cellules F16: F18, vous voyez les ventes moyennes, selon l’emplacement de l’affichage. Lorsque l’affichage est à l’avant de la section du livre d’ordinateur, les ventes moyennes sont de 900; lorsque l’affichage est à l’arrière de la section, les ventes atteignent en moyenne 1 400; et lorsque l’affichage est au milieu, les ventes atteignent en moyenne 1 100 ventes. Étant donné que la valeur de p de 0,003 (dans la cellule H23) est inférieure à 0,15, vous pouvez conclure que ces moyennes sont significativement différentes.

Si je détermine si les populations ont des moyens significativement différents, pourquoi la technique s’appelle-t-elle analyse de la variance?

Supposons que les données de votre étude de vente de livres soient les données affichées dans la feuille de calcul nommée Insig, illustrée à la figure 4 (et dans le Onewayan   fichier ova.xlsx). Si vous exécutez une ANOVA unidirectionnelle sur ces données, vous obtenez les résultats indiqués dans la figure 5.

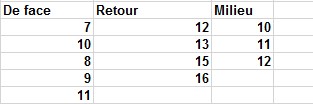
FIGURE 4 Données de librairie pour lesquelles l’hypothèse nulle est acceptée.

Notez que les ventes moyennes pour chaque partie du magasin sont exactement les mêmes qu’avant, mais la valeur de p de 0,66 indique que vous devez accepter l’hypothèse nulle et conclure que la position de l’affichage dans la section du livre d’ordinateur n’affecte pas les ventes . La raison de ce résultat étrange est que dans le deuxième ensemble de données, vous avez beaucoup plus de variations dans les ventes lorsque l’affichage est à chaque position dans la section du livre d’ordinateur. Dans le premier ensemble de données, par exemple, la variation des ventes lorsque l’affichage est à l’avant se situe entre 700 et 1 100, alors que dans le deuxième ensemble de données, la variation des ventes se situe entre 200 et 2000. La variation des ventes dans chaque position de magasin est mesurée par la somme des carrés de données au sein d’un groupe. Cette mesure est indiquée dans la cellule D24 du premier ensemble de données et dans la cellule F24 du second.

Dans le premier ensemble de données, la somme des carrés de données dans les groupes n’est que de 22, alors que dans le second ensemble de données, la somme des carrés dans les groupes est de 574! Cette grande variation dans les points de données à chaque position de magasin masque la variation entre les groupes (positions de magasin) eux-mêmes et rend impossible de conclure pour le deuxième ensemble de données que la différence entre les ventes dans différentes positions de magasin est significative.

FIGURE 5 Résultats ANOVA acceptant l’hypothèse nulle.

Comment puis-je utiliser les résultats d’une ANOVA unidirectionnelle pour les prévisions?

S’il existe une différence significative entre les moyennes des groupes, la meilleure prévision pour chaque groupe est simplement

moyenne du groupe. Par conséquent, dans le premier ensemble de données, vous prédisez les éléments suivants:

■■ Les ventes lorsque l’écran est à l’avant de la section des livres informatiques seront de 900 livres par semaine.

■■ Les ventes lorsque l’écran est à l’arrière seront de 1 400 livres par semaine.

■■ Les ventes lorsque l’écran est au milieu seront de 1 100 livres par semaine.

S’il n’y a pas de différence significative entre les moyennes du groupe, votre meilleure prévision pour chaque observation est simplement la moyenne globale. Ainsi, dans le deuxième ensemble de données, vous prédisez des ventes hebdomadaires de 1 117, indépendamment de l’emplacement des livres.

Vous pouvez également estimer l’exactitude de vos prévisions. La racine carrée de l’intérieur des groupes MS (carré moyen) est l’écart type des prévisions d’une ANOVA unidirectionnelle. Comme le montre la figure 3, l’écart-type des prévisions pour le premier ensemble de données est de 1,56 (voir à nouveau la feuille de travail Signifie). En règle générale, cela signifie que vous vous attendez, par exemple:

■■ Pendant 68% de toutes les semaines pendant lesquelles les livres sont placés à l’avant de la section des livres informatiques, les ventes se situeront entre 900 – 156 = 744 et 900 + 156 = 1 056 livres.

■■ Pendant 95% de toutes les semaines pendant lesquelles les livres sont placés à l’avant de la section des livres informatiques, les ventes se situeront entre 900 – 2 (156) = 588 livres et 900 + 2 (156) = 1 212 livres.