Le degré auquel se comportent deux variables, c’est-à-dire la façon dont elles covarient, s’appelle la corrélation. Un exemple familier est la taille et le poids. Pour cette exemple, on a ce qu’on appelle une corrélation positive: des valeurs élevées

sur une variable sont associées à des valeurs élevées sur l’autre variable (voir la figure 4.1).

Figure 4.1. Une corrélation positive apparaît dans un graphique comme une tendance générale de la partie inférieure gauche vers la partie supérieure droite.

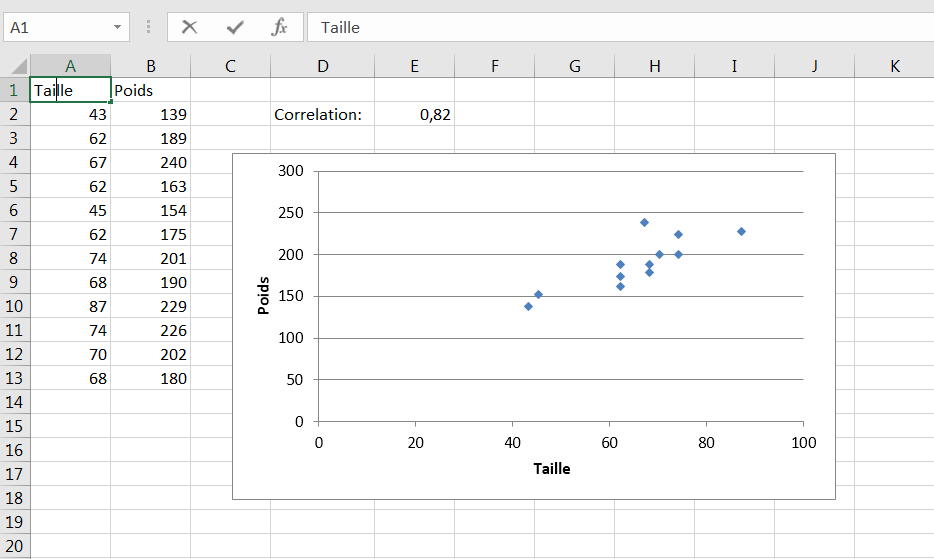
Le graphique de la figure 4.1 a un marqueur pour chacune des 12 personnes dont la taille et le poids apparaissent dans les cellules A2: B13. Généralement, plus la taille de la personne est basse (selon l’axe horizontal), plus le poids de la personne est bas (selon l’axe vertical) et plus la taille est grande, plus le poids est important.
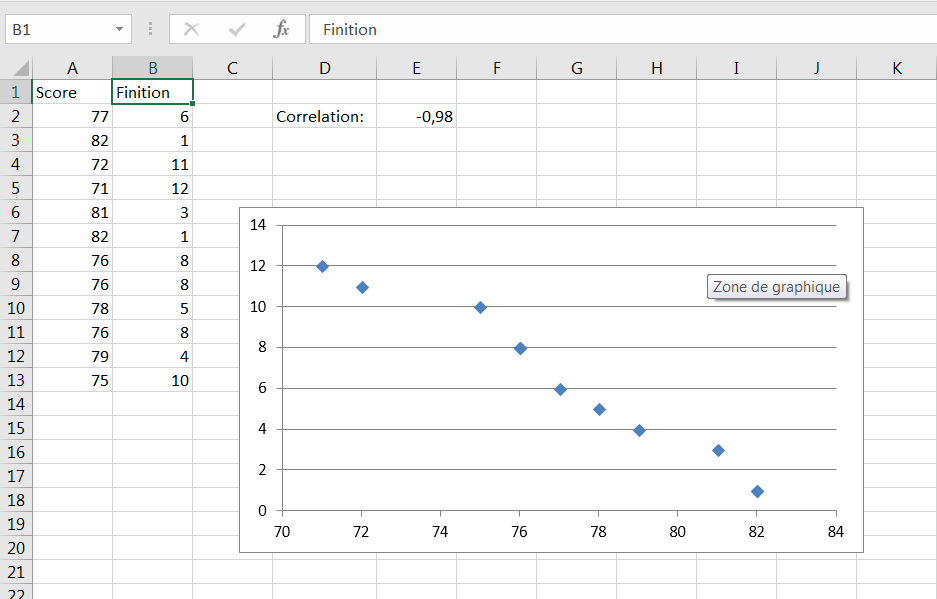
La situation inverse apparaît dans la figure 4.2, qui représente le nombre de points marqués dans une partie par rapport à l’ordre d’arrivée de chaque joueur. Plus le nombre de points est élevé, plus la finition est faible (c’est-à-dire meilleure). C’est un exemple de corrélation négative : des valeurs plus élevées sur une variable sont associées à des valeurs plus faibles sur l’autre variable.

Figure 4.2. Une corrélation négative apparaît comme une tendance générale de la partie supérieure gauche à la partie inférieure droite.
 

Notez la figure dans la cellule E2 des deux figures 4.1 et 4.2. C’est le coefficient de corrélation. Il exprime la force et la direction de la relation entre les deux variables. Dans la figure 4.1, le coefficient de corrélation est 0,82, un nombre positif. Par conséquent, les deux variables varient dans la même direction : un coefficient de corrélation positif indique que des valeurs plus élevées sur une variable sont associées à des valeurs plus élevées sur l’autre variable.
Dans la figure 4.2, le coefficient de corrélation est de -0,98, un nombre négatif. Par conséquent, la relation entre les deux variables est négative, indiquée par la direction de la tendance dans le graphique de la figure 4.2. Des valeurs plus élevées sur une variable sont associées à des valeurs plus faibles sur l’autre variable.
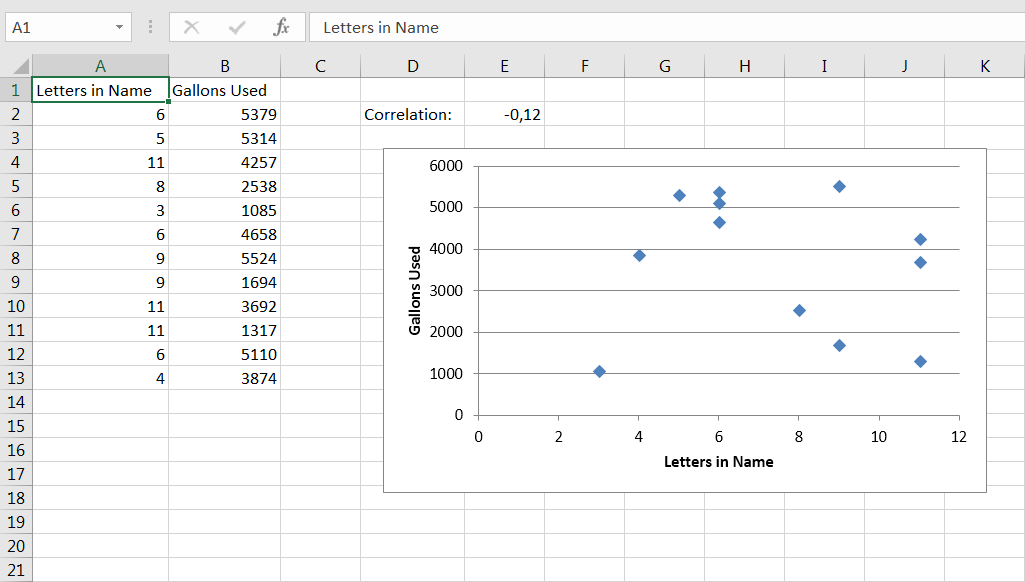
Le coefficient de corrélation, noté r peut prendre des valeurs comprises entre -1,0 et +1,0. Plus on se rapproche de plus ou moins 1,0, plus la relation est forte. Lorsque deux variables ne sont pas liées, la corrélation que vous pourriez calculer entre les deux devrait être proche de 0.0. Par exemple, la figure 4.3 montre la relation entre le nombre de lettres dans le nom de famille d’une personne et le nombre de gallons d’eau que ce ménage utilise dans un mois.

Figure 4.3. Deux variables non corrélées tendent à afficher une relation telle que celle-ci: une projection aléatoire de marqueurs sur le graphique.