Syntaxe. ACOSH(nombre)
Définition.
Cette fonction renvoie le cosinus hyperbolique inverse d’un nombre (voir Figure). La plage de définition s’étend de x= +1 à +œ.
Argument
■ nombre(obligatoire) Un nombre réel égal ou supérieur à 1.
Arrière-plan.
Les fonctions hyperboliques inverses sont également appelées fonctions hyperboliques d’aire. Ce sont les fonctions inverses des fonctions hyperboliques. Les fonctions hyperboliques sinh, tanh et coth sont strictement monotones et ont une fonction inverse. La fonction cosh, cependant, a deux intervalles monotones symétriques au segment positif de l’ordonnée et deux fonctions inverses :
y= arcsh x et y= -arcosh x
où :
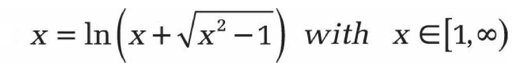
Le graphique (voir Figure) commence au point 1.0 et est monotone croissant ou décroissant.
REMARQUE
Les fonctions hyperboliques inverses ont le préfixe ar de la même manière que les fonctions trigonométriques inverses ont le préfixe arc. Les notations sinh^-1 cosh^-1 ou tanh^-1 sont également utilisées.
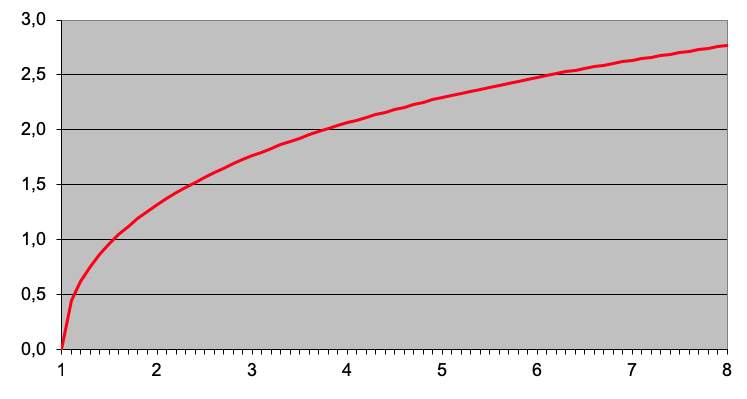
Illustration. Le graphique de l’arcosh montre le segment croissant de monotonie dans le premier quadrant. La monotonie
le segment décroissant est situé en sens inverse sous l’abscisse.
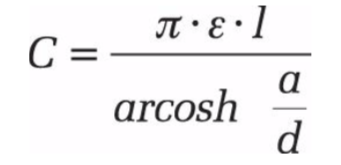
D’autres exemples de cette fonction sont :
=ACOSH(1) renvoie 0.
=ACOSH(2) renvoie 3169579.
=ACOSH(8) renvoie 76865938.
