Imaginez qu’on vous fournit un grand nombre de données différentes et on vous demande de prédire les chiffres de vente de votre entreprise l’année prochaine. Vous avez découvert des dizaines, voire des centaines de facteurs qui peuvent éventuellement affecter les chiffres. Mais comment savoir lesquels sont vraiment importants ? Exécutez une analyse de régression dans Excel. Il vous donnera une réponse à cette question et à bien d’autres : quels facteurs sont importants et lesquels peuvent être ignorés ? Dans quelle mesure ces facteurs sont-ils liés les uns aux autres ? Et dans quelle mesure pouvez-vous être sûr des prédictions ?
1 Analyse de régression dans Excel : les bases
Dans la modélisation statistique, l’analyse de régression est utilisée pour estimer les relations entre deux variables ou plus :
■La variable dépendante (alias variable de critère ) est le principal facteur que vous essayez de comprendre et de prédire.
■Les variables indépendantes (également appelées variables explicatives ou prédicteurs) sont les facteurs susceptibles d’influencer la variable dépendante.
L’analyse de régression vous aide à comprendre comment la variable dépendante change lorsque l’une des variables indépendantes varie et permet de déterminer mathématiquement laquelle de ces variables a réellement un impact.
Un modèle d’analyse de régression est basé sur la somme des carrés, qui est une méthode mathématique pour trouver la dispersion des points de données. Le but d’un modèle est d’obtenir la plus petite somme de carrés possible et de tracer une ligne qui se rapproche le plus des données.
En statistique, ils font la différence entre une régression linéaire simple et multiple. La régression linéaire simple modélise la relation entre une variable dépendante et une variable indépendante à l’aide d’une fonction linéaire. Si vous utilisez deux ou plusieurs variables explicatives pour prédire la variable dépendante, vous avez affaire à une régression linéaire multiple. Si la variable dépendante est modélisée comme une fonction non linéaire parce que les relations de données ne suivent pas une ligne droite, utilisez plutôt la régression non linéaire.
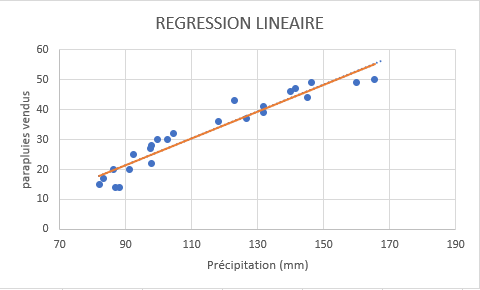
À titre d’exemple, prenons les chiffres des ventes de parapluies au cours des 24 derniers mois et découvrons les précipitations mensuelles moyennes pour la même période. Tracez ces informations sur un graphique et la ligne de régression démontrera la relation entre la variable indépendante (précipitations) et la variable dépendante (ventes parapluie) :
2 Équation de régression linéaire
Mathématiquement, une régression linéaire est définie par cette équation :
y = bx + a + ε
Où:
■ x est une variable indépendante.
■ y est une variable dépendante.
■ a est l’ordonnée à l’origine, qui est la valeur moyenne attendue de y lorsque toutes les variables x sont égales à 0. Sur un graphique de régression, c’est le point où la ligne croise l’axe Y.
■ b est la pente d’une droite de régression, qui est le taux de variation de y lorsque x change.
■ ε est le terme d’erreur aléatoire, qui est la différence entre la valeur réelle d’une variable dépendante et sa valeur prédite.
L’équation de régression linéaire a toujours un terme d’erreur car, dans la vie réelle, les prédicteurs ne sont jamais parfaitement précis. Cependant, certains programmes, y compris Excel, effectuent le calcul du terme d’erreur dans les coulisses. Ainsi, dans Excel, vous effectuez une régression linéaire en utilisant la méthode des moindres carrés et recherchez les coefficients a et b tels que :
y = bx + a
Pour notre exemple, l’équation de régression linéaire prend la forme suivante :
Parapluies vendus = b * précipitations + a
Il existe une poignée de façons différentes de trouver a et b . Les trois principales méthodes pour effectuer une analyse de régression linéaire dans Excel sont :
■ Outil de régression inclus avec Analysis ToolPak
■ Nuage de points avec une ligne de tendance
■ Formule de régression linéaire
Vous trouverez ci-dessous les instructions détaillées sur l’utilisation de chaque méthode.
3 Faire une régression linéaire dans Excel avec Analysis ToolPak
Cet exemple montre comment exécuter la régression dans Excel à l’aide d’un outil spécial inclus avec le complément Analysis ToolPak.
3.1 Activer le complément Analysis ToolPak
Analysis ToolPak est disponible dans toutes les versions d’Excel 2019 à 2003 mais n’est pas activé par défaut. Vous devez donc l’activer manuellement. Voici comment:
- Dans votre Excel, cliquez sur Fichier / Options.
- Dans la boîte de dialogue Options Excel , sélectionnez Compléments dans la barre latérale gauche, assurez -vous que Compléments Excel est sélectionné dans la zone Gérer , puis cliquez sur Accéder.
3.Dans la boîte de dialogue Compléments, cochez Analysis Toolpak etcliquez sur OK.
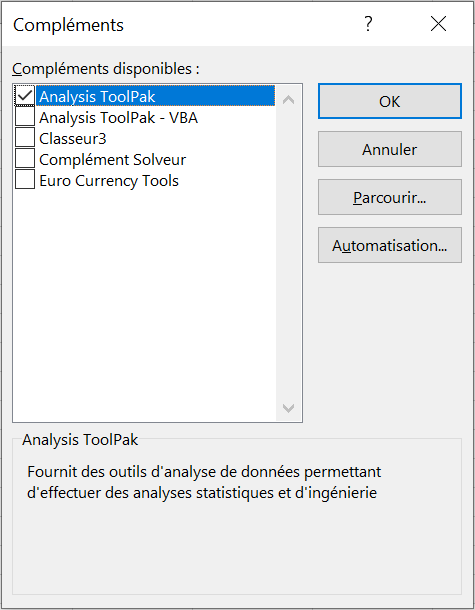
Cela ajoutera les outils d’analyse de données à l’onglet Données de votre ruban Excel.
3.2 Exécuter une analyse de régression
Dans cet exemple, nous allons faire une régression linéaire simple dans Excel. Nous avons une liste des précipitations mensuelles moyennes des 24 derniers mois dans la colonne B, qui est notre variable indépendante (prédicteur), et le nombre de parapluies vendus dans la colonne C, qui est la variable dépendante. Bien sûr, de nombreux autres facteurs peuvent affecter les ventes, mais pour l’instant, nous nous concentrons uniquement sur ces deux variables :
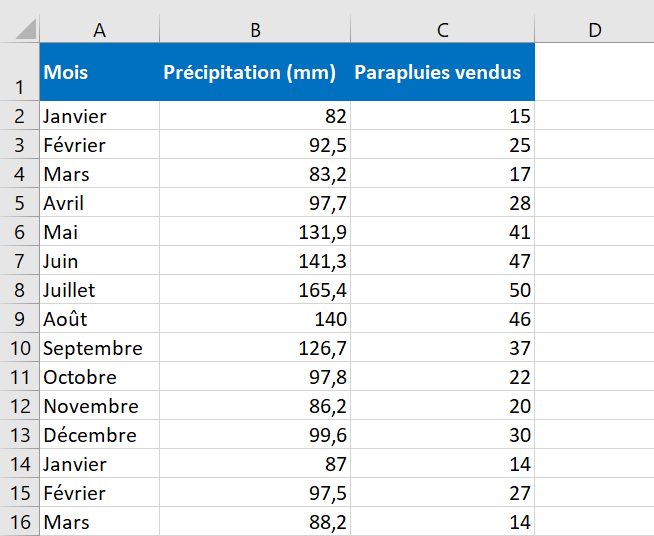
Avec Analysis Toolpak ajouté et activé, effectuez ces étapes pour effectuer une analyse de régression dans Excel :
- Dans l’onglet Données , dans le groupe Analyse, cliquez sur le bouton Utilitaire d’analyse.
2.Sélectionnez Régressionlinéaire et cliquez sur OK. 
3.Dans la boîte de dialogue Régression linéaire, configurez les paramètres suivants :
- Sélectionnez la plage pour la variable Y, qui est votre variable dépendante. Dans notre cas, il s’agit de ventes parapluie (C1:C25).
- Sélectionnez la Plage pour les variables X, c’est-à-dire votre variable indépendante. Dans cet exemple, il s’agit des précipitations mensuelles moyennes (B1:B25).
Si vous construisez un modèle de régression multiple, sélectionnez deux ou plusieurs colonnes adjacentes avec des variables indépendantes différentes.
- Cochez la case Intitulé présent s’il y a des en-têtes en haut de vos plages X et Y.
- Choisissez votre option de sortie préférée, une nouvelle feuille de calcul dans notre cas.
- Si vous le souhaitez, cochez la case Résiduspour obtenir la différence entre les valeurs prévues et réelles.
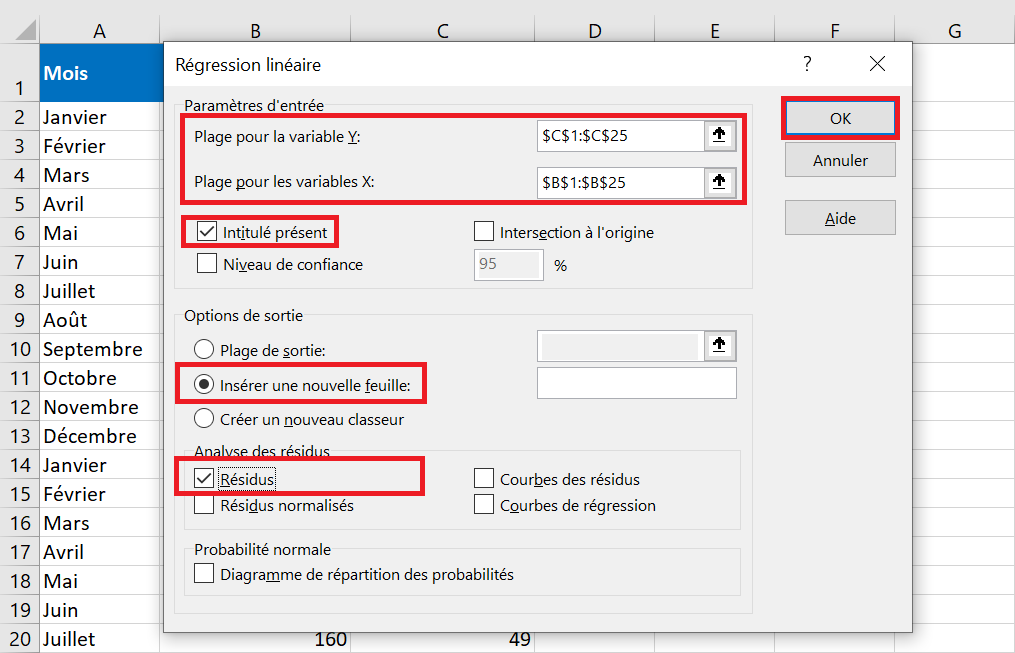
- Cliquez sur OKet observez la sortie de l’analyse de régression créée par Excel.
3.3 Interpréter les résultats de l’analyse de régression
Comme vous venez de le voir, exécuter la régression dans Excel est facile car tous les calculs sont effectués automatiquement. L’interprétation des résultats est un peu plus délicate car il faut savoir ce qui se cache derrière chaque chiffre. Vous trouverez ci-dessous une ventilation de 4 parties principales de la sortie de l’analyse de régression.
3.3.1 Sortie de l’analyse de régression : sortie récapitulative
Cette partie vous indique dans quelle mesure l’équation de régression linéaire calculée correspond à vos données source.

Voici ce que chaque élément d’information signifie :
■ Coefficient de détermination multiple : C’est le coefficient de corrélation qui mesure la force d’une relation linéaire entre deux variables. Le coefficient de corrélation peut être n’importe quelle valeur entre -1 et 1, et sa valeur absolue indique la force de la relation. Plus la valeur absolue est grande, plus la relation est forte :
- 1 signifie une relation positive forte
- -1 signifie une forte relation négative
- 0 signifie aucune relation
■ Coefficient de détermination R^2 : C’est le coefficient de détermination, qui est utilisé comme indicateur de la qualité de l’ajustement. Il montre combien de points tombent sur la ligne de régression. La valeur R
2 est calculée à partir de la somme totale des carrés, plus précisément, c’est la somme des écarts au carré des données d’origine par rapport à la moyenne.
Dans notre exemple, R2 est 0,91 (arrondi à 2 chiffres), ce qui est assez bon. Cela signifie que 91 % de nos valeurs correspondent au modèle d’analyse de régression. Autrement dit, 91 % des variables dépendantes (valeurs y) sont expliquées par les variables indépendantes (valeurs x). Généralement, un R au carré de 95 % ou plus est considéré comme un bon ajustement.
■ Coefficient de détermination R^2 ajusté : C’est le R carré ajusté du nombre de variables indépendantes dans le modèle. Vous voudrez utiliser cette valeur au lieu de R carré pour l’analyse de régression multiple.
■ Erreur type . Il s’agit d’une autre mesure de la qualité de l’ajustement qui montre la précision de votre analyse de régression – plus le nombre est petit, plus vous pouvez être certain de votre équation de régression. Alors que R 2 représente le pourcentage de la variance des variables dépendantes qui est expliquée par le modèle, l’erreur standard est une mesure absolue qui montre la distance moyenne à laquelle les points de données tombent de la ligne de régression.
■ Observations : Il s’agit simplement du nombre d’observations dans votre modèle.
3.3.2 Résultat de l’analyse de régression : ANOVA
La deuxième partie de la sortie est l’analyse de la variance (ANOVA) :

Il divise la somme des carrés en composants individuels qui donnent des informations sur les niveaux de variabilité au sein de votre modèle de régression :
■ Degré de liberté (df) est le nombre de degrés de liberté associés aux sources de variance.
■ Somme des carrés (SS) est la somme des carrés. Plus la SS résiduelle est petite par rapport à la SS totale, mieux votre modèle correspond aux données.
■ Moyennes des carrés (MS) est le carré moyen.
■ F est la statistique F ou F-test pour l’hypothèse nulle. Il est utilisé pour tester la signification globale du modèle.
■ Valeur critique de F est la valeur P de F.
La partie ANOVA est rarement utilisée pour une simple analyse de régression linéaire dans Excel, mais vous devez absolument examiner de près le dernier composant. La valeur Signifiance F donne une idée de la fiabilité (statistiquement significative) de vos résultats. Si la signification F est inférieure à 0,05 (5 %), votre modèle est OK. S’il est supérieur à 0,05, vous feriez probablement mieux de choisir une autre variable indépendante.
3.3.3 Résultat de l’analyse de régression : coefficients
Cette section fournit des informations spécifiques sur les composants de votre analyse :

Le composant le plus utile de cette section est Coefficients . Il vous permet de construire une équation de régression linéaire dans Excel :
y = bx + a
Pour notre ensemble de données, où y est le nombre de parapluies vendus et x est une pluviométrie mensuelle moyenne, notre formule de régression linéaire est la suivante :
Y = Coefficient de précipitations * x + Interception
Muni des valeurs a et b arrondies à trois décimales, il se transforme en :
Y=0.45*x -19.074
Par exemple, avec une pluviométrie mensuelle moyenne égale à 82 mm, les ventes de parapluies seraient d’environ 17,8 :
0.45*82-19.074=17.8
De la même manière, vous pouvez savoir combien de parapluies seront vendus avec toute autre pluviométrie mensuelle (x variable) que vous spécifiez.
3.3.4 Résultat de l’analyse de régression : résidus
Si vous comparez le nombre estimé et réel de parapluies vendus correspondant à une pluviométrie mensuelle de 82 mm, vous verrez que ces chiffres sont légèrement différents :
■ Estimation : 17,8 (calculé ci-dessus)
■Réel : 15 (ligne 2 des données source)
Pourquoi la différence ? Parce que les variables indépendantes ne sont jamais des prédicteurs parfaits des variables dépendantes. Et les résidus peuvent vous aider à comprendre à quelle distance les valeurs réelles sont des valeurs prédites :
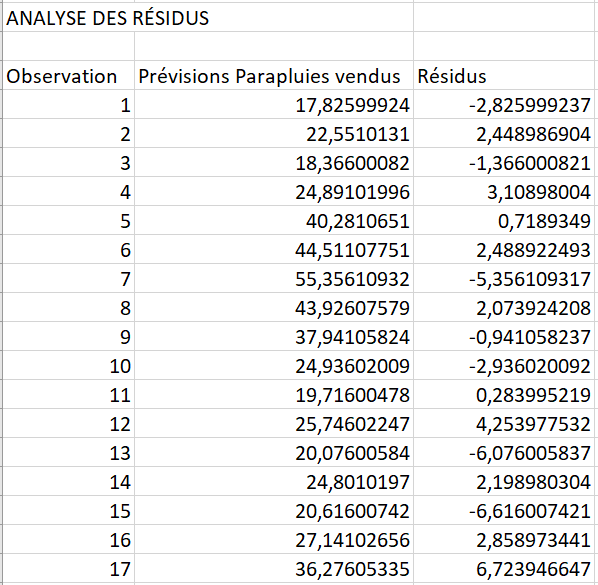
Pour le premier point de données (précipitations de 82 mm), le résidu est d’environ -2,8. Donc, nous ajoutons ce nombre à la valeur prédite et obtenons la valeur réelle : 17,8 – 2,8 = 15.
4 Comment faire un graphique de régression linéaire
Si vous avez besoin de visualiser rapidement la relation entre les deux variables, dessinez un graphique de régression linéaire. C’est très facile ! Voici comment:
- Sélectionnez les deux colonnes avec vos données, y compris les en-têtes.
- Dans l’onglet Insertion, dans le groupe graphique, cliquez sur l’icône Nuage de points et sélectionnez la vignette nuage de point (la première) :
Cela insérera un nuage de points dans votre feuille de calcul, qui ressemblera à celui-ci :
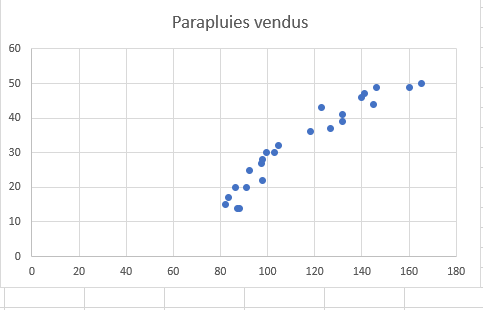
- Maintenant, nous devons tracer la droite de régression des moindres carrés. Pour ce faire, faites un clic droit sur n’importe quel point et choisissez Ajouter une ligne de tendance…dans le menu contextuel.
4.Dans le volet de droite, sélectionnez la forme de la courbe de tendance linéaire et, éventuellement, cochez Afficher l’équation sur le graphique pour obtenir votre formule de régression :
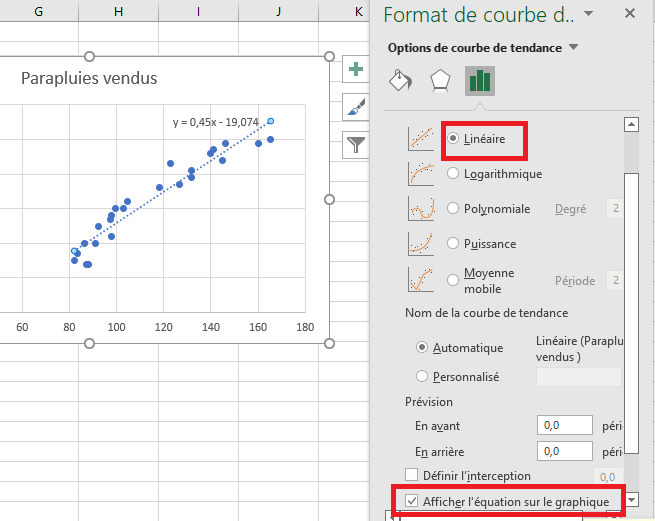
Comme vous pouvez le remarquer, l’équation de régression qu’Excel a créée pour nous est la même que la formule de régression linéaire que nous avons construite sur la base de la sortie Coefficients .
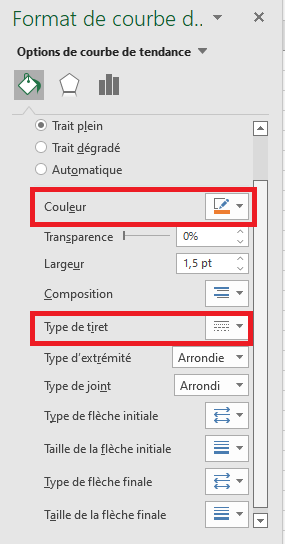
- Passez à l’onglet Remplissage et ligne et personnalisez la ligne à votre guise. Par exemple, vous pouvez choisir une couleur de ligne différente et utiliser une ligne continue au lieu d’une ligne pointillée (sélectionnez Ligne continue dans la zone Type de tiret ) :
À ce stade, votre graphique ressemble déjà à un graphique de régression décent :
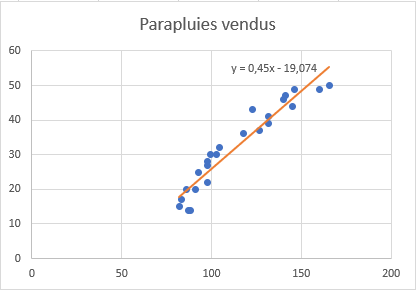
Néanmoins, vous voudrez peut-être apporter quelques améliorations supplémentaires :
- Faites glisser l’équation où bon vous semble.
- Ajoutez des titres d’axes ( bouton Éléments du graphique / Titres d’axes ).
- Si vos points de données commencent au milieu de l’axe horizontal et/ou vertical comme dans cet exemple, Et voici à quoi ressemble notre graphique de régression amélioré :
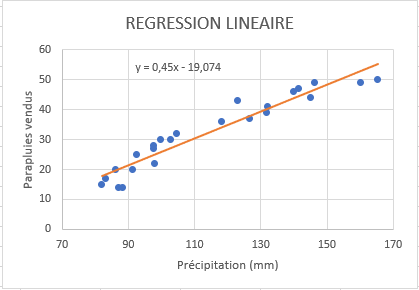
Dans le graphique de régression, la variable indépendante doit toujours être sur l’axe X et la variable dépendante sur l’axe Y. Si votre graphique est tracé dans l’ordre inverse, permutez les colonnes dans votre feuille de calcul, puis dessinez à nouveau le graphique. Si vous n’êtes pas autorisé à réorganiser les données source, vous pouvez basculer les axes X et Y directement dans un graphique.
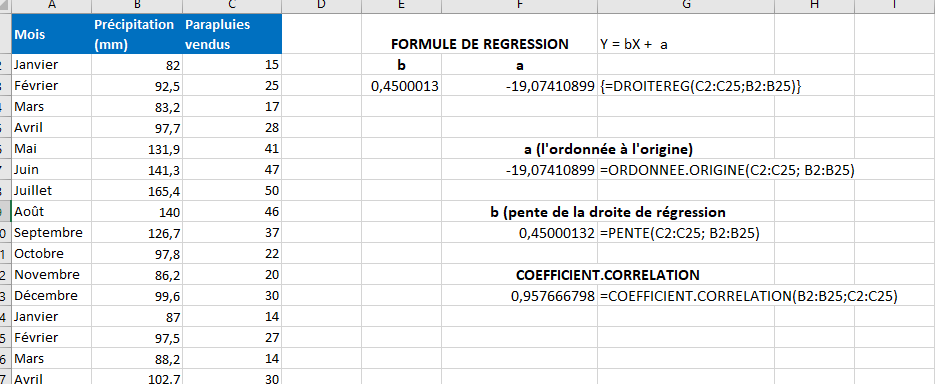
5 Faire une régression en utilisant des formules
Microsoft Excel dispose de quelques fonctions statistiques qui peuvent vous aider à effectuer une analyse de régression linéaire telles que DROITEREG( ), PENTE( ), ORDONNEE.ORIGINE( ) et COEFFICIENT.CORRELATION( ).
La fonction DROITEREG( ) utilise la méthode de régression des moindres carrés pour calculer une ligne droite qui explique le mieux la relation entre vos variables et renvoie un tableau décrivant cette ligne.
Pour l’instant, créons simplement une formule pour notre exemple d’ensemble de données :
=DROITEREG(C2:C25 ;B2:B25)
Étant donné que la fonction DROITEREG( ) renvoie un tableau de valeurs, vous devez le saisir sous la forme d’une formule matricielle . Sélectionnez deux cellules adjacentes dans la même ligne, E2:F2 dans notre cas, tapez la formule et appuyez sur Ctrl + Maj + Entrée pour le compléter.
La formule renvoie le coefficient b (E2) et la constante a (F2) pour l’équation de régression linéaire déjà familière :
y = bx + a
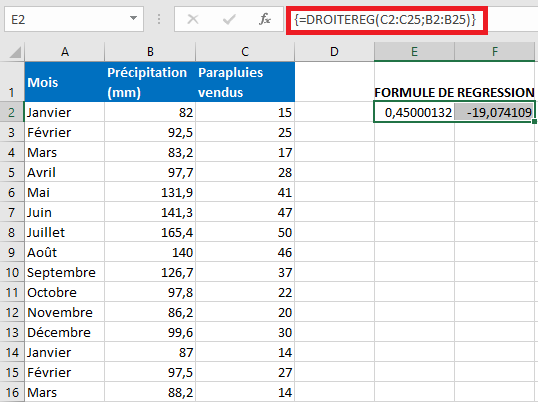
Si vous évitez d’utiliser des formules matricielles dans vos feuilles de calcul, vous pouvez calculer a et b individuellement avec des formules régulières :
Obtenez l’ordonnée à l’origine (a) :
=ORDONNEE.ORIGINE(C2:C25; B2:B25)
Obtenez la pente (b):
=PENTE(C2:C25; B2:B25)
De plus, vous pouvez trouver le coefficient de corrélation ( Multiple R dans la sortie récapitulative de l’analyse de régression ) qui indique à quel point les deux variables sont liées l’une à l’autre :
=COEFFICIENT.CORRELATION(B2:B25;C2:C25)
La capture d’écran suivante montre toutes ces formules de régression Excel en action :