blocs randomisés et bidirectionnels ANOVA
J’essaie d’analyser l’efficacité de ma force de vente. Le problème est qu’en plus de l’efficacité d’un représentant commercial, le montant qu’il vend dépend du quartier auquel il est affecté. Comment puis-je intégrer les affectations de district de mes représentants dans mon analyse?
■■ Sur la base de mes connaissances des commerciaux et des districts, comment puis-je prévoir les ventes? Quelle est la précision de mes prévisions de ventes?
■■ Comment puis-je déterminer si la variation du prix et de la quantité de publicité affecte les ventes d’un jeu vidéo? Comment puis-je déterminer si le prix et la publicité interagissent de manière significative?
■■ Comment puis-je interpréter les effets du prix et de la publicité sur les ventes lors d’interactions importantes
entre le prix et la publicité est absent?
Dans de nombreux ensembles de données, deux facteurs peuvent influencer une variable dépendante. Voici quelques exemples:

| Lorsque deux facteurs peuvent influencer une variable dépendante, des blocs randomisés ou une analyse de variance bidirectionnelle (ANOVA) peuvent être utilisés pour déterminer lesquels, le cas échéant, des facteurs ont une influence significative sur la variable dépendante. Avec l’ANOVA bidirectionnelle, vous pouvez également déterminer si deux facteurs présentent une interaction significative. Par exemple, supposons que vous essayez de prédire les ventes en utilisant le prix du produit et le budget publicitaire. Le prix et la publicité interagissent de manière significative si l’effet de la publicité dépend du prix du produit.
Dans un modèle de bloc aléatoire, vous observez chaque combinaison possible de facteurs exactement une fois. Vous ne pouvez pas tester les interactions dans une conception de bloc chaque combinaison de facteurs le même nombre de fois (appelez-le k). Dans ce cas, k doit être supérieur à 1. Dans un modèle ANOVA bidirectionnel, vous pouvez facilement tester les interactions. |
|
J’essaie d’analyser l’efficacité de ma force de vente. Le problème est qu’en plus de l’efficacité d’un représentant commercial, le montant qu’il vend dépend du district auquel il est affecté. Comment puis-je intégrer les affectations de district de mes représentants dans mon analyse?
Supposons que vous souhaitiez déterminer comment un commercial et le district de vente auquel le représentant est affecté influencent les ventes de produits. Pour répondre à la question de cet exemple, vous pouvez demander à chacun des quatre commerciaux de passer un mois à vendre dans chacun des cinq districts de vente. Les ventes qui en résultent sont indiquées dans la feuille de calcul Blocs randomisés du fichier Twowayanova.xlsx et illustrées à la figure 1. Par exemple, la représentante 1 a vendu 20 unités au cours du mois où elle a été affectée au district 4.
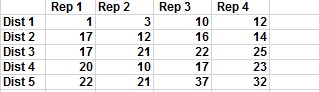
FIGURE 1 Données pour l’exemple des blocs randomisés.
Ce modèle est appelé ANOVA bidirectionnelle sans réplication car deux facteurs (district et représentant commercial) peuvent influencer les ventes et vous ne disposez que d’une seule instance associant chaque représentant à chaque district. Ce modèle est également appelé conception de blocs aléatoires parce que vous aimeriez randomiser (chronologiquement) l’affectation des représentants aux districts. En d’autres termes, vous souhaitez vous assurer que le mois au cours duquel le représentant 1 est affecté au district 1 est également susceptible d’être le premier, le deuxième, le troisième, le quatrième ou le cinquième mois. Espérons que cette randomisation atténue l’effet du temps sur votre analyse; dans un sens, vous bloquez l’effet des quartiers lorsque vous essayez de comparer les commerciaux.
Pour analyser ces données dans Microsoft Excel, cliquez sur Analyse des données dans l’onglet Données, puis sélectionnez Anova: deux facteurs sans réplication. Remplissez la boîte de dialogue comme illustré à la figure 2.
Vous pouvez utiliser les informations suivantes pour configurer cette analyse:
■■ Les données de la plage d’entrée se trouvent dans les cellules C5: G10.
■■ Sélectionnez Étiquettes car la première ligne de la plage d’entrée contient des étiquettes.
■■ Entrez B12 comme cellule supérieure gauche de la plage de sortie.
■■ La valeur alpha détermine le nombre indiqué dans la colonne F Crit. Vous n’aurez pas besoin des informations de la colonne F Crit. Par conséquent, tout au long de ce chapitre, vous pouvez utiliser la valeur alpha par défaut de 0,05.
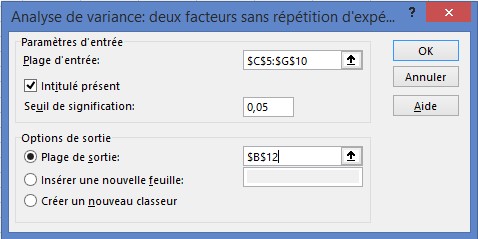
FIGURE 2 Anova: boîte de dialogue à deux facteurs sans réplication pour configurer un modèle de blocs randomisés.
La sortie que vous obtenez est illustrée à la figure 3. (Les résultats dans les cellules G12: G24 n’ont pas été créés par la fonction d’analyse des données Excel. Des formules ont été entrées dans ces cellules, comme expliqué plus loin dans l’article.)
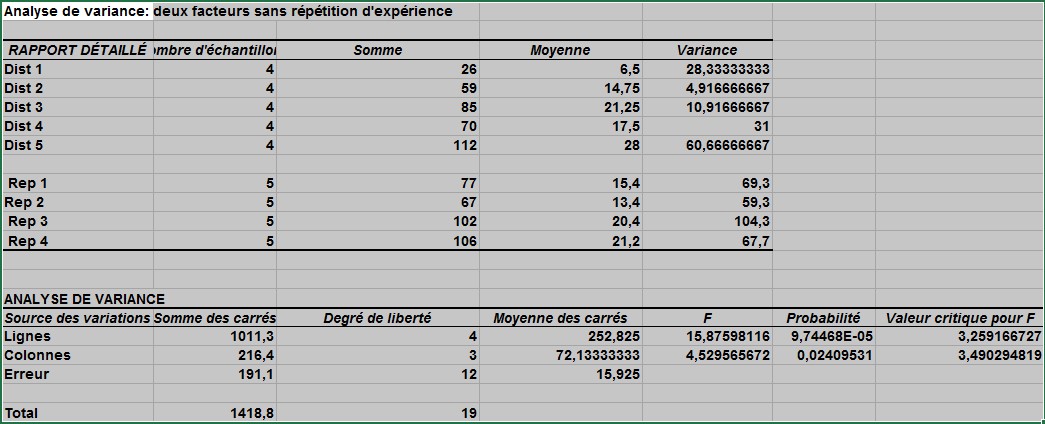
FIGURE 3 Sortie de blocs randomisés.
Pour déterminer si le facteur de ligne (districts) ou le facteur de colonne (représentants des ventes) a un effet significatif sur ventes, il suffit de regarder la valeur p. Si la valeur de p pour un facteur est faible (inférieure à 0,15), le facteur a un effet significatif sur les ventes. La valeur p de la ligne (.0000974) et la valeur p de la colonne (.024) sont toutes deux inférieures à .15, de sorte que le district et le représentant ont un effet significatif sur les ventes.
Sur la base de ma connaissance des commerciaux et des districts, comment puis-je prévoir les ventes? Quelle est la précision de mes prévisions de ventes?
Comment prévoir les ventes de produits? Vous pouvez prédire les ventes au cours d’un mois en utilisant l’équation 1, illustrée ici:
Ventes prévues = Moyenne globale + (effet Rep) + (effet District)
Dans cette équation, l’effet Rep est égal à 0 si le facteur représentant des ventes n’est pas significatif. Si le facteur représentant des ventes est significatif, l’effet représentant est égal à la moyenne pour le représentant donné moins la moyenne globale. De même, l’effet de district est égal à 0 si le facteur de district n’est pas significatif. Si le facteur de district est significatif, l’effet de district est égal à la moyenne du district donné moins la moyenne globale.
Calculez la moyenne globale (17,6) dans la cellule G12 en utilisant la formule MOYENNE (D6: G10). Les effets représentatifs et de district sont calculés en copiant la formule E15– $ G $ 12 de la cellule G15 à G16: G24. Par exemple, vous pouvez calculer les ventes prévues par le représentant 4 dans le district 2 comme 17,6 – 2,85 + 3,6 = 18.35. Cette valeur est calculée dans la cellule D38 (voir figure 61-4) avec la formule G12 + G16 + G24. Si laedistrict est important et l’effet représentant des ventes ne l’est pas, ventes prévues pour le représentant 4 dans le district 2 serait 17,6 – 2,85 = 14,75.

FIGURE 4 Prévisions des ventes dans le district 2 par le représentant 4.
Comme dans l’ANOVA unidirectionnelle, l’écart type des erreurs de prévision est la racine carrée de l’erreur quadratique moyenne indiquée dans la cellule E31. Vous pouvez calculer cet écart-type dans la cellule E32 avec la formule SQRT (E31). Ainsi, vous pouvez être sûr à 95% que si Rep 4 est affecté au district 2, les ventes mensuelles seront comprises entre 18,35 – 2 (3,99) = 10,37 et 18,35 + 2 (3,99) = 26,33. Ces limites sont calculées dans les cellules D39 et D40 avec les formules D38–2 * E32 et D38 + 2 * E32, respectivement.
Comment puis-je déterminer si la variation du prix et de la quantité de publicité affecte les ventes d’un jeu vidéo? Comment puis-je déterminer si le prix et la publicité interagissent de manière significative?
Lorsque vous avez plusieurs observations pour chaque combinaison des facteurs de ligne et de colonne, vous disposez d’une ANOVA à deux facteurs avec réplication. Pour effectuer ce type d’analyse, Excel requiert que vous ayez le même nombre d’observations pour chaque combinaison de lignes et de colonnes.
En plus de tester la signification des facteurs de ligne et de colonne, vous pouvez également tester l’interaction significative entre eux. Par exemple, si vous voulez comprendre comment le prix et la publicité affectent les ventes, une interaction entre le prix et la publicité indiquerait que l’effet d’un changement de publicité dépendrait du niveau de prix (ou, de manière équivalente, l’effet d’un changement de prix serait dépendent du niveau de publicité). Un manque d’interaction entre le prix et la publicité signifierait que l’effet d’un changement de prix ne dépendrait pas du niveau de la publicité.
À titre d’exemple d’ANOVA à deux facteurs avec réplication, supposons que vous souhaitiez déterminer comment le prix et le niveau publicitaire affectent les ventes mensuelles d’un jeu vidéo. Dans la feuille de calcul Two Way ANOVA No Interaction du fichier Twowayanova.xlsx, vous pouvez trouver les données illustrées dans la figure 61-5. Pendant les trois mois durant lesquels la publicité était faible et le prix moyen, par exemple, 21, 20 et 16 unités ont été vendues.
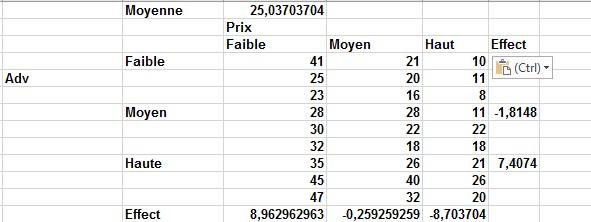
FIGURE 5 Données de vente de jeux vidéo; aucune interaction.
Notez que pour chaque combinaison prix / publicité, il y a exactement trois observations. Dans la cellule D1, la moyenne globale (25,037) de toutes les observations avec la formule MOYENNE (D4: F12) est calculée. Dans les cellules G4, G7 et G10, l’effet pour chaque niveau de publicité est calculé. Par exemple, l’effet d’avoir un faible niveau de publicité est égal à la moyenne pour une faible publicité moins la moyenne globale. Dans la cellule G4, le faible effet publicitaire de –5,59 avec la formule MOYENNE (D4: F6) – $ D $ 1 est calculé. Dans de façon similaire, l’effet de chaque niveau de prix en copiant la formule MOYENNE (D4: D12) – $ D $ 1 de D13 à E13: F13 est calculé.
Pour analyser ces données, cliquez sur Analyse des données dans l’onglet Données, puis sélectionnez Anova: deux facteurs Avec réplication dans la boîte de dialogue Analyse des données. Remplissez la boîte de dialogue comme illustré à la figure 6.
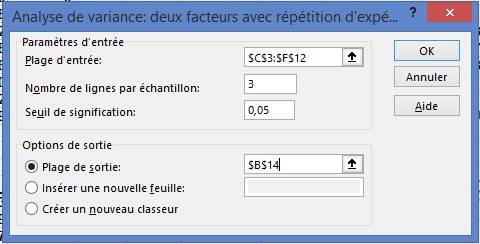
FIGURE 6 Anova: boîte de dialogue à deux facteurs avec réplication pour exécuter une ANOVA à deux facteurs avec réplication.
Vous pouvez utiliser les informations suivantes pour configurer l’analyse:
■■ Les données de la plage d’entrée, y compris les étiquettes, sont en C3: F12. Dans l’ANOVA bidirectionnelle avec réplication, Excel requiert une étiquette pour chaque niveau de l’effet de colonne dans la première ligne de chaque colonne de la plage d’entrée. Ainsi, vous pouvez entrer Large, Moyen et Grand dans les cellules D3: F3 pour indiquer l’éventuel niveaux de prix. Excel requiert également une étiquette pour chaque niveau de l’effet de ligne dans la première colonne de la plage d’entrée. Ces étiquettes doivent apparaître dans la ligne qui marque le début des données pour chaque niveau. Ainsi, vous pouvez placer des étiquettes correspondant à des niveaux de publicité faibles, moyens et élevés dans les cellules C4, C7 et C10.
■■ Dans la zone Lignes par échantillon, entrez 3 car vous disposez de trois réplications pour chaque combinaison de prix et de niveau de publicité.
■■ La cellule supérieure gauche de votre plage de sortie est B14.
La seule partie importante de la sortie est le tableau ANOVA, qui est illustré à la figure 7.

FIGURE 7 ANOVA bidirectionnelle avec sortie de réplication; aucune interaction.
Comme pour les blocs randomisés, un effet (y compris les interactions) est significatif s’il a une valeur de p inférieure à 0,15. Ici, Échantillon (c’est la ligne pour l’effet publicitaire) et Prix (montré dans la ligne intitulée Colonnes) sont très significatifs et il n’y a pas d’interaction significative. (La valeur p d’interaction est 0,79!) Par conséquent, vous pouvez conclure que le prix et la publicité influencent les ventes et que l’effet de la publicité sur les ventes ne dépend pas du niveau des prix. La figure 61-8 représente les ventes moyennes pour chaque combinaison de publicité par prix et montre que le prix et la publicité ne présentent pas d’interaction significative. (Voir la feuille de calcul Graphique sans interaction.)
Notez que lorsque la publicité augmente, les ventes moyennes augmentent à peu près au même rythme, que le niveau de prix soit bas, moyen ou élevé. Fondamentalement, vous pouvez reconnaître No Interaction par le fait que les séries pour chaque niveau de prix sont presque parallèles.
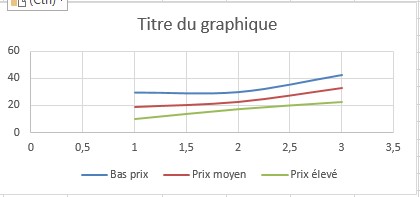
FIGURE 8 Aucune interaction entre le prix et la publicité dans cet ensemble de données.
Comment puis-je interpréter les effets du prix et de la publicité sur les ventes lors d’une interaction significative entre le prix et la publicité est absent?
En l’absence d’interaction significative, vous pouvez prévoir les ventes dans une ANOVA à deux facteurs avec réplication de la même manière que vous le faites dans une ANOVA à deux facteurs sans réplication. Voici l’équation à utiliser (équation 2):
Ventes prévues = Moyenne globale + [Effet de ligne ou de publicité (si significatif)] + [Colonne ou effet prix (si significatif)]
Cette analyse suppose que le prix et la publicité sont les seuls facteurs qui affectent les ventes. Si les ventes sont hautement saisonnières, la saisonnalité devrait être intégrée à l’analyse. (La saisonnalité est discutée au chapitre 63, «Méthode des hivers», et au chapitre 65, «Prévision en présence d’événements spéciaux».) Par exemple, lorsque le prix est élevé et que la publicité est moyenne, les ventes prévues sont données par 25,037 + (–1,814) + (–8,704) = 14,52. (Voir la cellule E54 de la figure 61-9, qui montre à nouveau la feuille de calcul ANOVA bidirectionnelle sans interaction.) Dans la figure 61-5, illustrée précédemment, vous pouvez voir que la moyenne globale est égale à 25,037, l’effet publicitaire moyen est égal à -1,814. , et l’effet prix élevé est égal à –8,704.
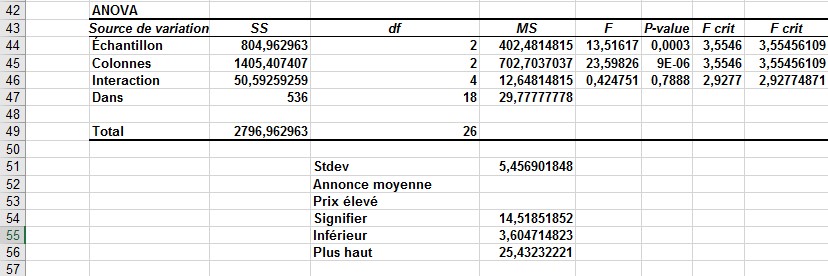
FIGURE 9 Prévisions de ventes à prix élevé et publicité moyenne.
L’écart type des erreurs de prévision est égal à la racine carrée de votre moyenne au carré dans l’erreur:
![]()
Vous pouvez être sûr à 95% que la prévision est exacte à 10,92 unités près. En d’autres termes, vous êtes 95% sûr que les ventes pendant un mois avec des prix élevés et une publicité moyenne seront entre 3,60 et 25,43 unités.
Dans la feuille de calcul ANOVA bidirectionnelle avec interaction, les données de l’exemple précédent ont été remplacées par celles de la figure 10. Après avoir exécuté l’analyse pour une ANOVA à deux facteurs avec réplication, les résultats montrés sur la figure 11 ont été obtenus.
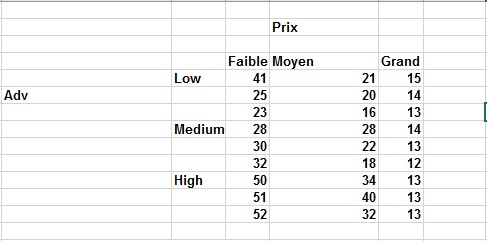
FIGURE 10 Données de vente avec interaction entre prix et publicité.

FIGURE 11 Sortie pour l’ANOVA à deux facteurs avec interaction.
Dans cet ensemble de données, la valeur de p pour l’interaction est de 0,001. Lorsque vous voyez une faible valeur de p (inférieure à 0,15) pour l’interaction, vous ne vérifiez même pas les valeurs de p pour les facteurs de ligne et de colonne. Vous prévoyez simplement des ventes pour n’importe quelle combinaison de prix et de publicité égale à la moyenne des trois observations impliquant cette combinaison de prix et de publicité. Par exemple, la meilleure prévision de ventes pendant un mois avec une publicité élevée et un prix moyen est:
(34 + 40 + 32)/4 = 106 = 35,555 unités 4 3
L’écart type des erreurs de prévision est à nouveau la racine carrée du carré moyen à l’intérieur de:
![]()
Ainsi, vous pouvez être sûr à 95% que les prévisions de ventes sont exactes à 8,26 unités près.
La figure 12 montre pourquoi ces données présentent une interaction significative entre le prix et la publicité. Pour un prix bas et moyen, l’augmentation de la publicité augmente les ventes moyennes, mais si le prix est élevé, l’augmentation de la publicité n’a aucun effet sur les ventes moyennes. Cela explique pourquoi vous ne pouvez pas utiliser l’équation 2 pour prévoir les ventes lorsqu’une interaction significative est présente. Après tout, comment pouvez-vous parler d’un effet publicitaire lorsque l’effet de la publicité dépend du prix?
L’essentiel à noter sur ce graphique est que les différentes séries ne sont pas parallèles. Cela vous indique qu’à différents niveaux de prix, les changements dans la publicité ont des effets différents sur les ventes.
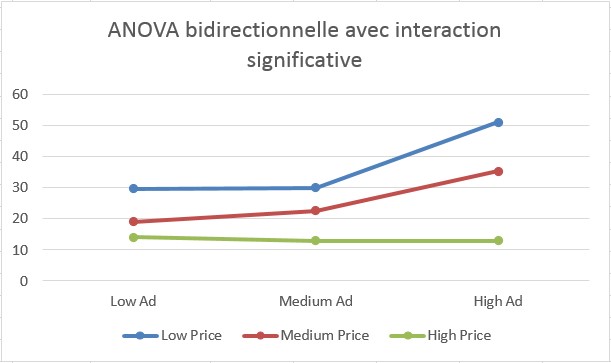
FIGURE 12 Le prix et la publicité présentent une interaction significative dans cet ensemble de données.
