Notez la formule dans la barre de formule illustrée à la figure 4.3:
=COEFFICIENT.CORRELATION(A2:A13;B2:B13)

Le fait que vous calculiez un coefficient de corrélation implique qu’il y a deux ou plusieurs variables à traiter – rappelez-vous que le coefficient de corrélation r exprime la force d’une relation entre deux variables. Vous trouverez deux variables dans les figures 4.1 à 4.3: l’une dans la colonne A, l’autre dans la colonne B.

Les arguments de la fonction COEFFICIENT.CORRELATION() indiquent où vous trouvez les valeurs de ces deux variables dans la feuille de calcul. Une variable, un ensemble de valeurs, est dans la première plage (A2: A13), et l’autre variable, et ses valeurs, dans la deuxième plage (B2: B13).
Dans les arguments de la fonction COEFFICIENT.CORRELATION(), la variable que vous identifiez en premier ne fait aucune différence. La formule qui calcule la corrélation de la figure 4.3 aurait tout aussi bien pu être la suivante:
= COEFFICIENT.CORRELATION (B2: B13, A2: A13)
Dans chaque ligne des plages que vous passez à COEFFICIENT.CORRELATION(), deux valeurs doivent être associées à la même personne ou objet. Dans la figure 4.1, qui montre une corrélation entre la taille et le poids, la rangée 2 pourrait avoir la taille de John dans la colonne A et son poids dans la colonne B; la rangée 3 pourrait avoir la hauteur de Pat dans la colonne A et le poids dans la colonne B, et ainsi de suite.
Le point important à reconnaître est que r exprime la force d’une relation entre deux variables. La seule façon de mesurer cette relation est de prendre les valeurs des variables sur un ensemble de personnes ou de choses et ensuite de maintenir l’appariement pour l’analyse statistique. Dans Excel, vous maintenez l’appariement correct en plaçant les deux mesures dans la même ligne. Vous pouvez calculer une valeur pour r si, par exemple, la taille de Jean était en A2 et son poids en B4, c’est-à-dire que les valeurs pourraient être dispersées de manière aléatoire dans les lignes, mais le résultat de votre calcul serait incorrect. Excel suppose que deux valeurs dans la même rangée d’une liste vont ensemble et qu’elles constituent une paire.

Dans le cas de la fonction COEFFICIENT.CORRELATION(), d’un point de vue purement mécanique, tout ce qui est vraiment nécessaire est que les observations associées occupent les mêmes positions relatives dans les deux tableaux. Si, pour une raison quelconque, vous vouliez utiliser A2: A13 et B3: B14 au lieu de A2: A13 et B2: B13, tout irait bien tant que les données de John sont en A2 et B3, Pat en A3 et B4, et ainsi sur.
Cependant, cette structure, A2: A13 et B3: B14, n’est pas conforme aux règles régissant les listes et les tableaux d’Excel. Comme je l’ai décrit, cette structure fonctionnerait, mais elle pourrait facilement revenir vous mordre. Sauf si vous avez des raisons impérieuses de faire autrement, gardez les mesures qui appartiennent à la même personne ou à un même objet dans la même rangée.

Remarque
Si vous avez l’habitude d’utiliser Excel pour calculer des statistiques, vous vous demandez peut-être quand ce chapitre va contourner la fonction PEARSON (). La réponse est que ce ne sera pas le cas. Excel a deux fonctions de feuille de calcul qui calculent r: COEFFICIENT.CORRELATION() et PEARSON (). Ils prennent les mêmes arguments et retournent exactement les mêmes résultats. Il n’y a pas de bonne raison pour cette fonctionnalité dupliquée : Quand j’ai informé un chef de produit chez Microsoft à ce sujet en 1995, il a répondu “Huh”.
Karl Pearson a développé le coefficient de corrélation renvoyé par les fonctions Excel COEFFICIENT.CORRELATION() et PEARSON () à la fin du XIXe siècle. Les abréviations r (pour la statistique) et [gr] (rho, le grec r, pour le paramètre) représentent la régression, une technique qui repose fortement sur la corrélation, et à propos de laquelle ce livre aura beaucoup plus à dire dans cette chapitres.

Tout ce que ce cours a à dire à propos de COEFFICIENT.CORRELATION() s’applique à PEARSON (). Je préfère COEFFICIENT.CORRELATION() simplement parce qu’il a moins de lettres à taper.
Ainsi, comme c’est le cas avec l’écart-type et la variance, Excel a une fonction qui calcule la corrélation en votre nom, et vous n’avez pas besoin de faire tout l’addition et la soustraction, la multiplication et la division de vous-même. Pourtant, un coup d’œil à l’une des formules de calcul pour r peut aider à donner un aperçu de ce dont il s’agit. La corrélation est basée sur la covariance, qui est symbolisée par s_xy:

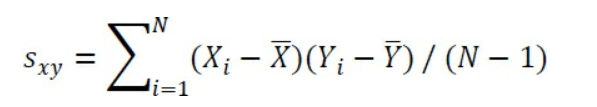
Cette formule peut vous sembler familière si vous avez lu le chapitre 3. Là, vous avez vu que la variance est calculée en soustrayant la moyenne de chaque valeur et en ajustant la déviation, c’est-à-dire multipliant la déviation par elle-même.

Remarque
Notez que le dénominateur dans la formule de la covariance est N – 1. La raison est la même que pour la variance, discutée au Chapitre 3: Dans un échantillon, à partir de laquelle vous voulez faire des inférences sur une population, les degrés de liberté au lieu de N est utilisé pour rendre l’estimation indépendante de la taille de l’échantillon. Excel 2010 à 2016 possède une fonction COVARIANCE.STANDARD () à utiliser avec un exemple de valeurs et une fonction COVARIANCE.PEARSON () à utiliser avec un ensemble de valeurs que vous considérez comme une population.
Dans le même ordre d’idées, notez à partir de sa formule que la covariance d’une variable avec elle-même est simplement la variance de la variable.
Pour voir l’effet du calcul de la covariance de cette manière, supposons que vous ayez deux variables, taille et poids, et une paire de mesures de ces variables pour chacun des deux hommes (voir Figure 44).

Figure 4.4. De grandes déviations sur une variable associée à de grandes déviations sur l’autre entraînent une covariance plus grande.

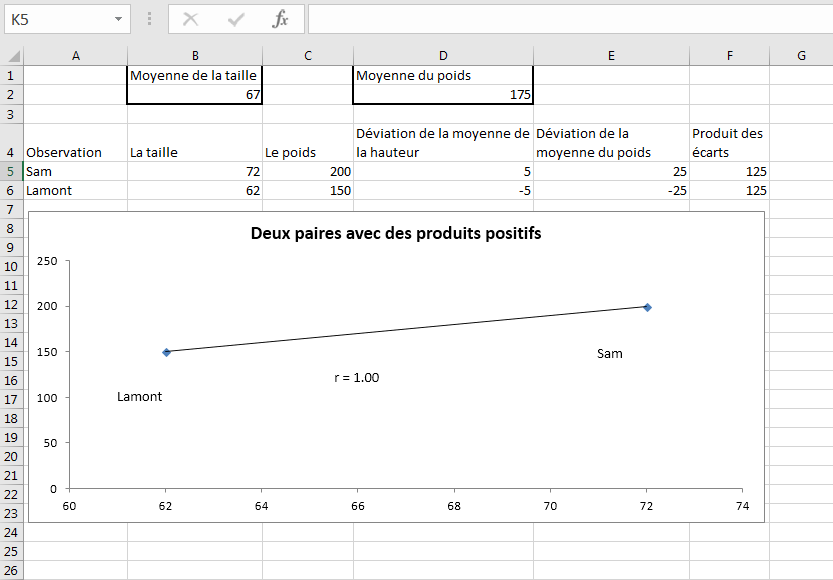
Dans la figure 4.4, une personne (Sam) pèse plus que le poids moyen de 175, et il est aussi plus grand que la taille moyenne de 67 pouces. Par conséquent, les deux scores de déviation de Sam, sa mesure moins la moyenne de cette mesure sera positive (voir les cellules D5 et E5 de la figure 4.4). Et donc, le résultat de ses scores d’écart doit aussi être positif (voir cellule F5).
En revanche, Lamont pèse moins que le poids moyen et est plus courte que la hauteur moyenne. Par conséquent, ses deux scores d’écart seront négatifs (cellules D6 et E6). Cependant, la règle pour multiplier deux nombres négatifs entre en jeu, et Lamont se retrouve avec un produit positif pour les scores d’écart dans la cellule F6.
Ces deux produits de déviation, qui sont tous les deux 125, sont totalisés dans ce fragment à partir de l’équation de la covariance (l’équation complète est donnée plus haut dans cette section):
 
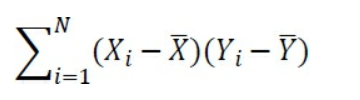
L’effet combiné de la sommation des deux produits de déviation est d’écarter la covariance d’une valeur de zéro: le produit de Sam de 125 le déplace de zéro, et le produit de Lamont, également 125, le déplace encore plus loin de zéro.
Notez la ligne diagonale dans le graphique de la figure 4.4. C’est ce qu’on appelle une ligne de régression (ou, en termes Excel, une ligne de tendance). Dans ce cas (comme c’est le cas de n’importe quel cas qui n’a que deux enregistrements), les deux marqueurs sur le graphique tombent directement sur la ligne de régression. Lorsque cela se produit, la corrélation est parfaite: +1,0 ou -1,0. Les corrélations parfaites sont le résultat soit de l’analyse de résultats triviaux (par exemple, la corrélation entre degrés Fahrenheit et degrés Celsius) ou d’exemples dans les manuels de statistiques. Le monde réel des mesures expérimentales est beaucoup plus désordonné.
On peut déduire une règle générale de cet exemple: Quand chaque paire de valeurs comporte deux écarts positifs, ou deux écarts négatifs, le résultat est que chaque enregistrement pousse la covariance, et donc le coefficient de corrélation, à partir de zéro et vers +1.0 . Ceci est comme il se doit: Plus la relation entre deux variables est forte, plus la corrélation est de 0,0. Plus les valeurs élevées d’une variable vont de l’autre avec des valeurs élevées (et les valeurs faibles d’une part avec des valeurs faibles d’autre part), plus la relation positive entre les deux variables est forte.
Qu’en est-il d’une situation dans laquelle chaque personne est relativement élevée sur une variable et relativement faible sur l’autre? Voir la figure 4.5 pour cette analyse.
Figure 4.5. La covariance est aussi forte que dans la figure 4.4, mais elle est négative.

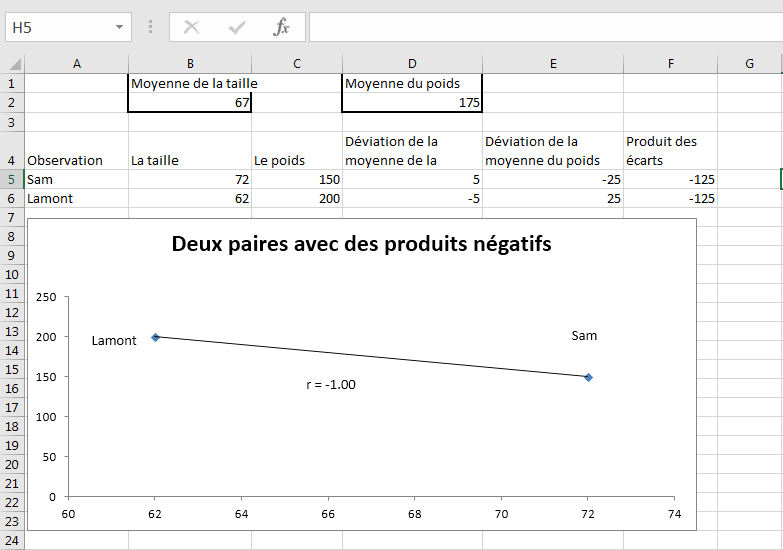
Dans la figure 4.5, la relation entre les deux variables a été inversée. Maintenant, Sam est toujours plus grand que la taille moyenne (écart positif en D5) mais pèse moins que le poids moyen (écart négatif en E5). Lamont est plus court que la hauteur moyenne (écart négatif en D6) mais pèse plus que le poids moyen (écart positif en E6).
Le résultat est que Sam et Lamont ont des produits de déviation négative en F5 et F6. Quand ils sont totalisés, leur effet combiné est d’éloigner la covariance de zéro. La relation est aussi forte que sur la figure 4.4, mais sa direction est différente. C’est négatif plutôt que positif.
La force de la relation entre les variables est mesurée par la taille de la corrélation et n’a rien à voir avec si la corrélation est positive ou négative. Par exemple, la corrélation entre le poids corporel et le nombre d’heures par semaine passées à faire du jogging pourrait être modérément forte. Mais il serait probablement négatif, peut-être -0,6, parce que vous vous attendriez à ce que plus le temps passé à faire du jogging moins le poids corporel.

Affaiblissement de la relation
La figure 4.6 montre ce qui se passe lorsque vous mélangez des produits positifs avec des produits à déviation négative.
Figure 4.6. Le produit de déviation de Peter est négatif, alors que ceux de Sam et Lamont sont toujours positifs.

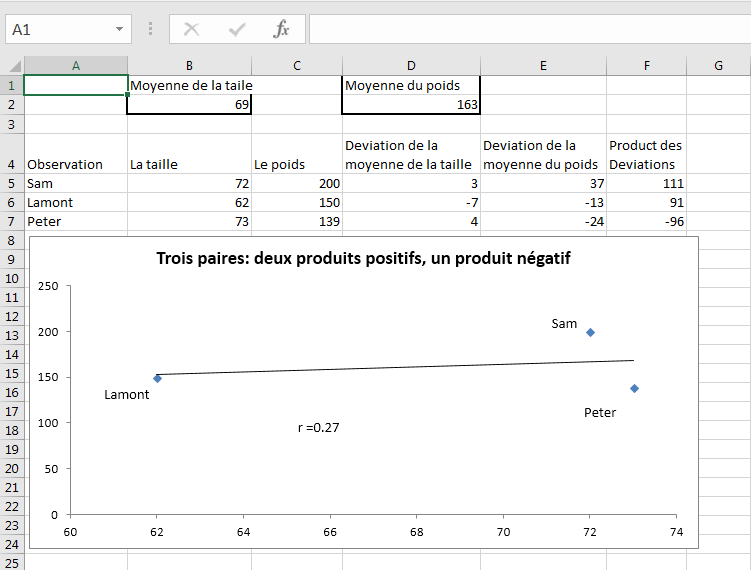
La figure 4.6 montre que les produits de déviation de Sam et Lamont sont toujours positifs (cellules F5 et F6). Cependant, ajouter Peter au mélange affaiblit la relation observée entre la taille et le poids. La taille de Peter est au-dessus de la moyenne, mais son poids est inférieur à la moyenne du poids. Le résultat est que son écart de hauteur est positif, son écart de poids est négatif, et le produit des deux est donc négatif.
Le produit négatif de Peter ramène la covariance vers zéro, étant donné que Sam et Lamont ont des produits de déviation positifs. C’est la preuve d’une relation plus faible entre la taille et le poids: les mesures de Peter nous disent que nous ne pouvons pas dépendre d’un couple de grande taille avec un poids lourd et une taille courte avec un poids faible, comme Sam et Lamont.
Lorsque la relation observée s’affaiblit, la covariance diminue aussi (elle est plus proche de zéro dans la figure 4.6 que dans les figures 4.4 et 45). Inévitablement (parce que le coefficient de corrélation est basé sur la covariance), le coefficient de corrélation se rapproche également de zéro: il est représenté par r dans les graphiques des figures 4.4 et 4.5, où il est parfait 1.0 et -1.0.
Dans la figure 4.6, r est beaucoup plus faible: .27 est une faible corrélation pour les variables continues telles que la taille et le poids.
Notez dans la figure 4.6 que les marqueurs de données de Sam et Peter ne touchent pas la ligne de régression. C’est un autre aspect d’une corrélation imparfaite: Les points de données tracés s’écartent de la ligne de régression. Corrélations imparfaites sont attendues avec des données du monde réel, et les écarts par rapport à la régression
ligne sont la règle, pas l’exception.