L’un des calculs statistiques les plus simples que vous puissiez effectuer dans Excel est la corrélation. Bien que simple, il est très utile pour comprendre les relations entre deux ou plusieurs variables. Microsoft Excel fournit tous les outils nécessaires pour exécuter une analyse de corrélation, il vous suffit de savoir comment les utiliser.
1 Les bases de la corrélation
La corrélation est une mesure qui décrit la force et la direction d’une relation entre deux variables. Il est couramment utilisé dans les statistiques, l’économie et les sciences sociales pour les budgets, les plans d’affaires, etc.
La méthode utilisée pour étudier à quel point les variables sont liées est appelée analyse de corrélation.
Voici quelques exemples de forte corrélation :
■Le nombre de calories que vous consommez et votre poids (corrélation positive)
■La température extérieure et vos factures de chauffage (corrélation négative)
Et voici les exemples de données qui ont une corrélation faible ou nulle :
■Le nom de votre chat et sa nourriture préférée
■La couleur de tes yeux et ta taille
Une chose essentielle à comprendre à propos de la corrélation est qu’elle montre seulement à quel point deux variables sont étroitement liées. Cependant, la corrélation n’implique pas la causalité. Le fait que les changements d’une variable soient associés à des changements dans l’autre variable ne signifie pas qu’une variable provoque réellement le changement de l’autre.
2. Coefficient de corrélation dans Excel : interprétation de la corrélation
La mesure numérique du degré d’association entre deux variables continues est appelée le coefficient de corrélation (r).
La valeur du coefficient est toujours comprise entre -1 et 1 et mesure à la fois la force et la direction de la relation linéaire entre les variables.
Force
Plus la valeur absolue du coefficient est grande, plus la relation est forte :
- Les valeurs extrêmes de -1 et 1 indiquent une relation linéaire parfaite lorsque tous les points de données tombent sur une ligne. En pratique, une corrélation parfaite, qu’elle soit positive ou négative, est rarement observée.
- Un coefficient de 0 indique qu’il n’y a pas de relation linéaire entre les variables. C’est ce que vous êtes susceptible d’obtenir avec deux ensembles de nombres aléatoires.
- Les valeurs comprises entre 0 et +1/-1 représentent une échelle de relations faibles, modérées et fortes. Lorsque r se rapproche de -1 ou 1, la force de la relation augmente.
Direction
Le signe du coefficient (plus ou moins) indique le sens de la relation.
- Les coefficients positifs représentent une corrélation directe et produisent une pente ascendante sur un graphique – à mesure qu’une variable augmente, l’autre augmente également, et vice versa.
- Les coefficients négatifs représentent une corrélation inverse et produisent une pente descendante sur un graphique – à mesure qu’une variable augmente, l’autre variable a tendance à diminuer.
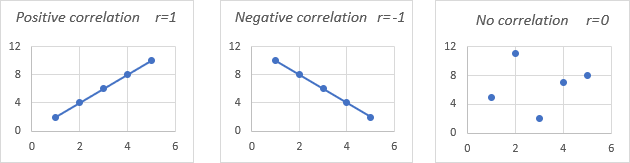
Pour une meilleure compréhension, veuillez consulter les graphiques de corrélation suivants :
- Un coefficient de 1 signifie une relation positive parfaite – à mesure qu’une variable augmente, l’autre augmente proportionnellement.
- Un coefficient de -1 signifie une relation négative parfaite – à mesure qu’une variable augmente, l’autre diminue proportionnellement.
- Un coefficient de 0 signifie qu’il n’y a pas de relation entre deux variables – les points de données sont dispersés sur tout le graphique.
3. Corrélation de Pearson
Dans les statistiques, ils mesurent plusieurs types de corrélation en fonction du type de données avec lesquelles vous travaillez. Dans cette section, nous allons nous concentrer sur le plus courant.
La corrélation de Pearson, dont le nom complet est Pearson Product Moment Correlation (PPMC), est utilisée pour évaluer les relations linéaires entre les données lorsqu’un changement dans une variable est associé à un changement proportionnel dans l’autre variable. En termes simples, la corrélation de Pearson répond à la question : les données peuvent-elles être représentées sur une ligne ?
Dans les statistiques, c’est le type de corrélation le plus populaire, et si vous avez affaire à un « coefficient de corrélation » sans autre qualification, il s’agit probablement du Pearson.
Voici la formule la plus couramment utilisée pour trouver le coefficient de corrélation de Pearson, aussi appelé R de Pearson :
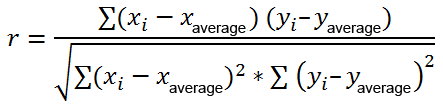
Parfois, vous pouvez rencontrer deux autres formules pour calculer le coefficient de corrélation de l’échantillon (r) et le coefficient de corrélation de la population (ρ).
Le calcul manuel du coefficient de corrélation de Pearson implique beaucoup de calculs. Heureusement, Microsoft Excel a rendu les choses très simples. En fonction de votre ensemble de données et de votre objectif, vous êtes libre d’utiliser l’une des techniques suivantes :
■ Trouvez le coefficient de corrélation de Pearson avec la fonction COEFFICIENT.CORRELATION ( ).
■ Créez une matrice de corrélation en effectuant une analyse de données.
■ Trouvez plusieurs coefficients de corrélation avec une formule.
■ Tracez un graphique de corrélation pour obtenir la représentation visuelle de la relation de données.
4 Calculer le coefficient de corrélation dans Excel
Pour trouver le coefficient de corrélation dans Excel, utilisez la fonction COEFFICIENT.CORRELATION ( ) ou PEARSON ( ) et obtenez le résultat en une fraction de seconde.
4.1 Fonction COEFFICIENT.CORRELATION ( )
La fonction COEFFICIENT.CORRELATION ( ) renvoie le coefficient de corrélation de Pearson pour deux ensembles de valeurs. Sa syntaxe est très simple et directe :
COEFFICIENT.CORRELATION (tableau1 ; tableau2)
Où:
■ tableau1 est la première plage de valeurs.
■ tableau2 est la deuxième plage de valeurs.
Les deux tableaux doivent avoir la même longueur.
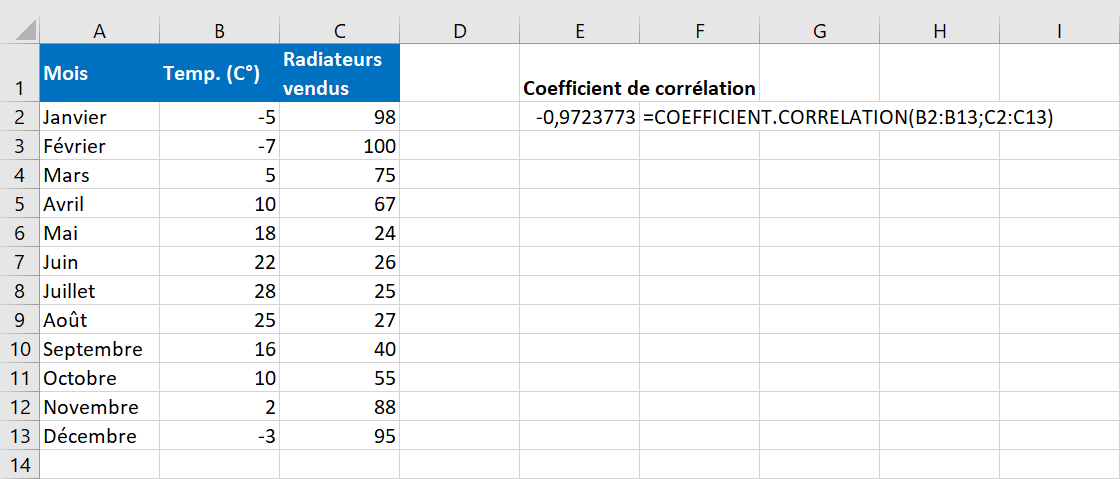
En supposant que nous ayons un ensemble de variables indépendantes ( x ) dans B2:B13 et de variables dépendantes (y) dans C2:C13, notre formule de coefficient de corrélation se présente comme suit :
= COEFFICIENT.CORRELATION (B2:B13 ; C2:C13)
Ou, nous pourrions échanger les plages et toujours obtenir le même résultat :
=COEFFICIENT.CORRELATION (C2:C13 ; B2:B13)
Dans tous les cas, la formule montre une forte corrélation négative (environ -0,97) entre la température mensuelle moyenne et le nombre d’appareils de chauffage vendus :
3 choses que vous devez savoir sur la fonction COEFFICIENT.CORRELATION( ) dans Excel
Pour calculer avec succès le coefficient de corrélation dans Excel, veuillez garder à l’esprit ces 3 faits simples :
■ Si une ou plusieurs cellules d’un tableau contiennent du texte, des valeurs logiques ou des blancs, ces cellules sont ignorées ; les cellules avec des valeurs nulles sont calculées.
■ Si les tableaux fournis sont de longueurs différentes, une erreur #N/A est renvoyée.
■ Si l’un des tableaux est vide ou si l’écart type de leurs valeurs est égal à zéro, un #DIV/0! erreur se produit.
4.2 Fonction PEARSON ( )
La fonction PEARSON dans Excel fait la même chose – calcule le coefficient Pearson.
= PEARSON (tableau1; tableau2)
Où:
■ tableau1 est une plage de valeurs indépendantes.
■ tableau2 est une plage de valeurs dépendantes.
Étant donné que PEARSON( ) et COEFFICIENT.CORRELATION( ) calculent tous deux le coefficient de corrélation linéaire de Pearson, leurs résultats doivent concorder, et ils le font généralement dans les versions récentes d’Excel 2007 à Excel 2019.
Dans Excel 2003 et les versions antérieures, cependant, la fonction PEARSON peut afficher des erreurs d’arrondi. Par conséquent, dans les anciennes versions, il est recommandé d’utiliser COEFFICIENT.CORRELATION de préférence à PEARSON.
Sur notre exemple d’ensemble de données, les deux fonctions présentent les mêmes résultats :
=COEFFICIENT.CORRELATION (B2:B13, C2:C13)
= PEARSON(B2:B13, C2:C13) 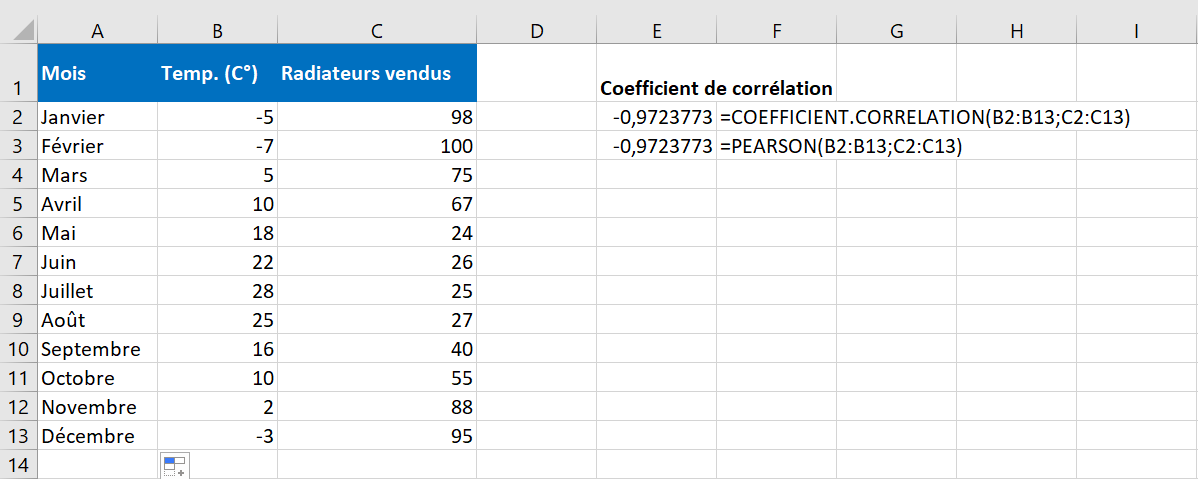
5. Créer une matrice de corrélation
Lorsque vous devez tester les interrelations entre plus de deux variables, il est judicieux de construire une matrice de corrélation, parfois appelée coefficient de corrélation multiple.
La matrice de corrélation est un tableau qui montre les coefficients de corrélation entre les variables à l’intersection des lignes et des colonnes correspondantes.
La matrice de corrélation dans Excel est créée à l’aide de l’ outil Corrélation du complément Analysis ToolPak . Ce complément est disponible dans toutes les versions d’Excel 2003 à Excel 2019, mais n’est pas activé par défaut. Si vous ne l’avez pas encore activé, veuillez le faire maintenant en suivant les étapes suivantes
- Dans votre Excel, cliquez sur Fichier / Options.
- Dans la boîte de dialogue Options Excel , sélectionnez Compléments dans la barre latérale gauche, assurez -vous que Compléments Excel est sélectionné dans la zone Gérer , puis cliquez sur Atteindre.
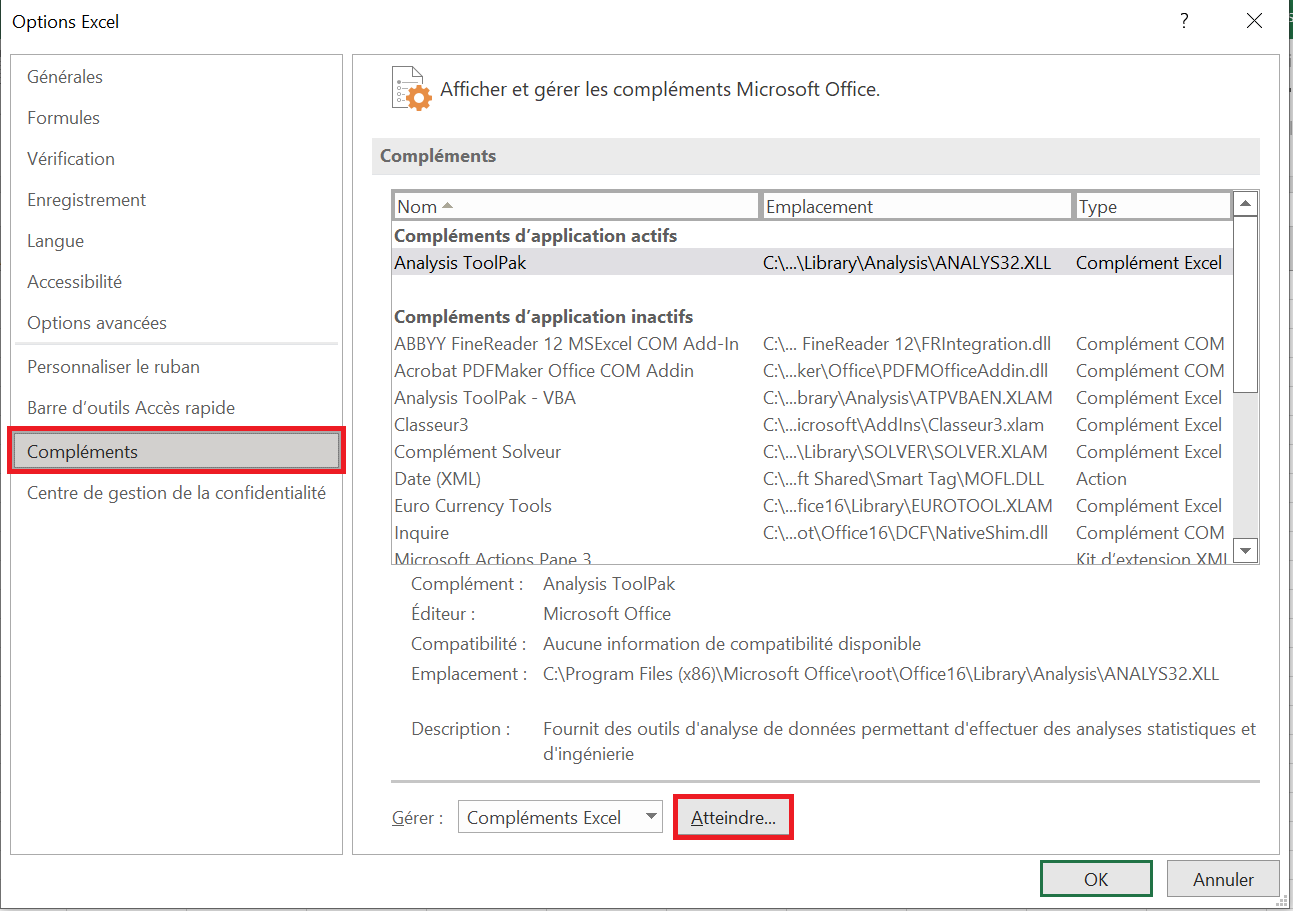
3.Dans la boîte de dialogue Compléments, cochez Analysis Toolpak et cliquez sur OK.
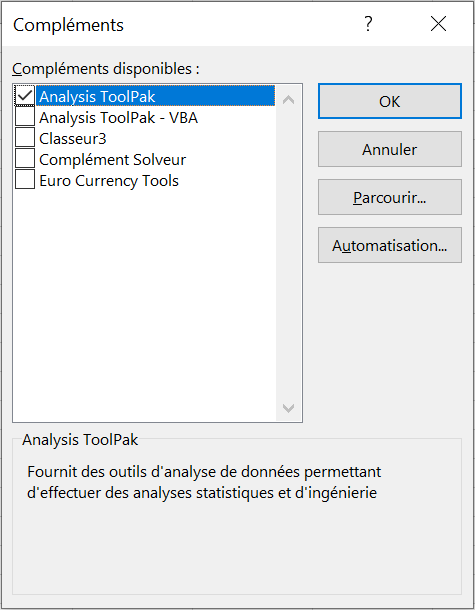
Cela ajoutera les outils d’analyse de données à l’onglet Données de votre ruban Excel.
Avec les outils d’analyse de données ajoutés à votre ruban Excel, vous êtes prêt à exécuter une analyse de corrélation :
- Dans le coin supérieur droit de l’ onglet Données / groupe Analyse , cliquez sur le bouton Utilitaire d’analyse.
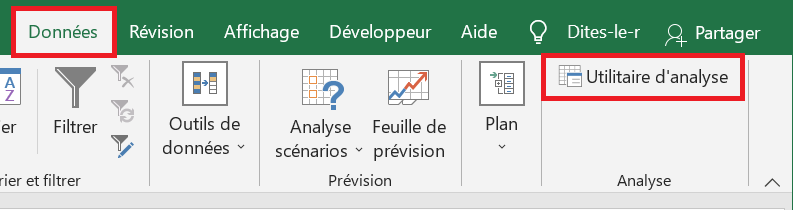
2.Dans la boîte de dialogue Analyse des données , sélectionnez Analyse de corrélation et cliquez sur OK.
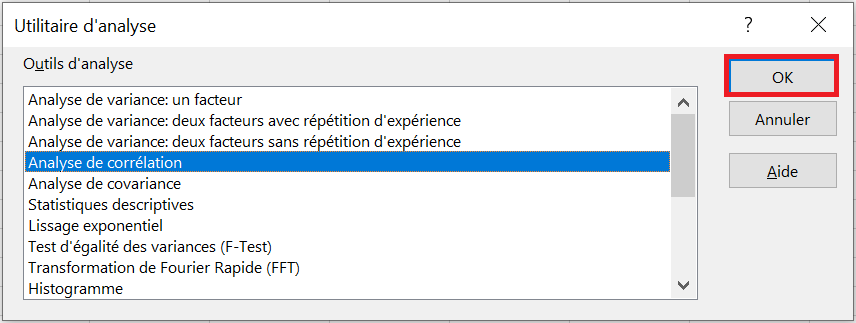
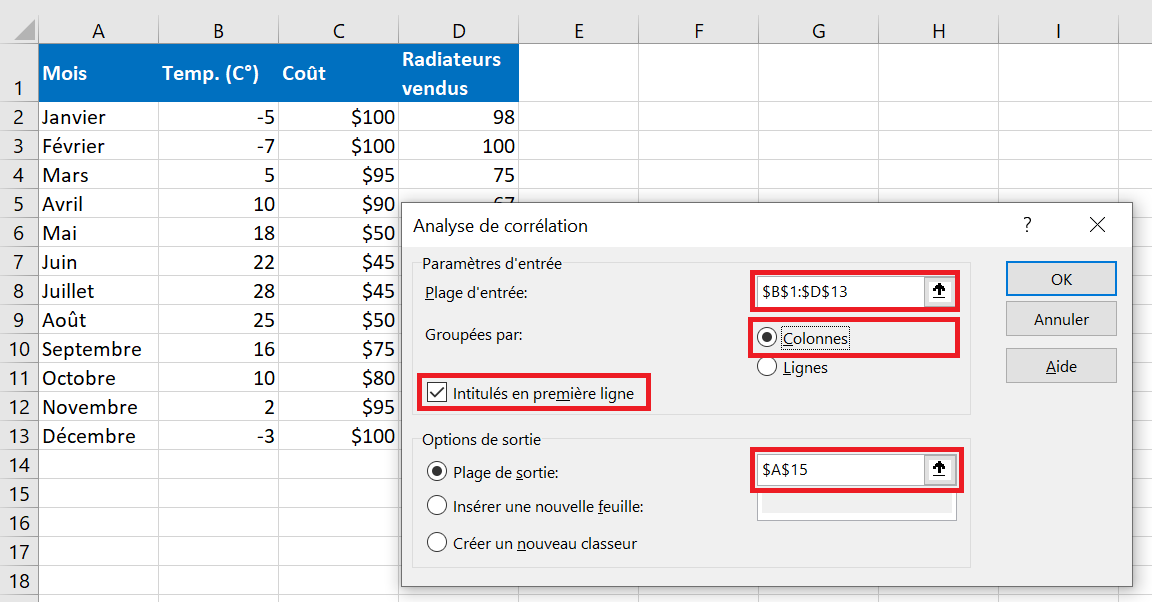
3.Dans la case Analyse de corrélation, configurez les paramètres de cette façon :
- Cliquez dans la zonePlage d’entrée et sélectionnez la plage avec vos données source, y compris les en-têtes de colonne (B1:D13 dans notre cas).
- Dans la section Groupés par, assurez-vous que la case d’option Colonnes est sélectionnée (étant donné que vos données source sont regroupées en colonnes).
- Cochez la case Intitulés en première ligne si la plage sélectionnée contient des en-têtes de colonne.
- Choisissez l’option de sortie souhaitée. Pour avoir la matrice dans la même feuille, sélectionnez Plage de sortieet spécifiez la référence à la cellule la plus à gauche dans laquelle la matrice doit être sortie (A15 dans cet exemple).
Une fois terminé, cliquez sur le bouton OK :
Votre matrice de coefficients de corrélation est terminée et devrait ressembler à celle illustrée dans la section suivante.
Interprétation des résultats de l’analyse de corrélation
Dans votre matrice de corrélation Excel, vous pouvez trouver les coefficients à l’intersection des lignes et des colonnes. Si les coordonnées de la colonne et de la ligne sont identiques, la valeur 1 est sortie.
Dans l’exemple ci-dessus, nous nous intéressons à la corrélation entre la variable dépendante (nombre d’appareils de chauffage vendus) et deux variables indépendantes (température mensuelle moyenne et frais de publicité). Ainsi, nous ne regardons que les nombres à l’intersection de ces lignes et colonnes, qui sont mis en évidence dans la capture d’écran ci-dessous :
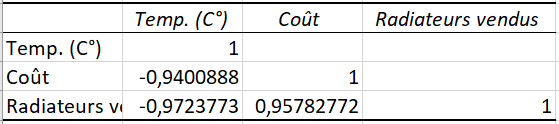
Le coefficient négatif de -0,97 (arrondi à 2 décimales) montre une forte corrélation inverse entre la température mensuelle et les ventes d’appareils de chauffage – à mesure que la température augmente, moins d’appareils de chauffage sont vendus.
Le coefficient positif de 0,97 (arrondi à 2 décimales) indique un lien direct étroit entre le budget publicitaire et les ventes : plus vous dépensez d’argent en publicité, plus les ventes sont élevées.
6. Faire une analyse de corrélation multiple avec des formules
Construire la table de corrélation avec l’outil d’analyse de données est facile. Cependant, cette matrice est statique, ce qui signifie que vous devrez exécuter une nouvelle analyse de corrélation chaque fois que les données source changent.
La bonne nouvelle est que vous pouvez facilement créer vous-même une table de corrélation similaire, et cette matrice se mettra à jour automatiquement à chaque modification des valeurs source.
Pour le faire, utilisez cette formule générique :
COEFFICIENT.CORRELATION (DECALER( Première_plage_variable ; 0; LIGNES($1:1)-1); DECALER( Première_plage_variable ; 0; COLONNES($A:A)-1))
Pour que la formule fonctionne, vous devez verrouiller la première plage de variables en utilisant des références de cellule absolues .
Dans notre cas, la première plage de variables est $B$2 :$B$13 (veuillez noter le signe $ qui verrouille la référence), et notre formule de corrélation prend cette forme :
=COEFFICIENT.CORRELATION(DECALER($B$2:$B$13; 0; LIGNES($1:1)-1); DECALER($B$2:$B$13; 0; COLONNES($A:A)-1))
Avec la formule prête, construisons une matrice de corrélation :
- Dans la première ligne et la première colonne de la matrice, saisissez les libellés des variables dans le même ordre qu’ils apparaissent dans votre tableau source (voir la capture d’écran ci-dessous).
- Entrez la formule ci-dessus dans la cellule la plus à gauche (B16 dans notre cas).
- Faites glisser la formule vers le bas et vers la droite pour la copier dans autant de lignes et de colonnes que nécessaire (3 lignes et 3 colonnes dans notre exemple).
En conséquence, nous avons la matrice suivante avec plusieurs coefficients de corrélation. Veuillez noter que les coefficients renvoyés par notre formule sont exactement les mêmes que ceux fournis par Excel dans l’ exemple précédent (les coefficients pertinents sont mis en surbrillance) : 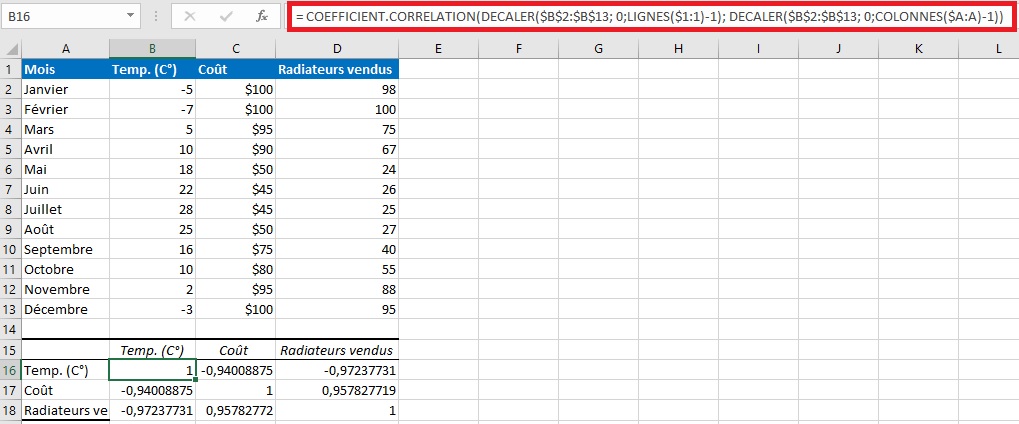
Comment fonctionne cette formule :
Comme vous le savez déjà, la fonction Coefficient.Correlation( ) renvoie le coefficient de corrélation pour deux ensembles de variables que vous spécifiez. Le principal défi consiste à fournir les plages appropriées dans les cellules correspondantes de la matrice. Pour cela, vous n’entrez que la première plage de variables dans la formule et utilisez les fonctions suivantes pour effectuer les ajustements nécessaires :
■ DECALER – renvoie une plage qui est un nombre donné de lignes et de colonnes à partir d’une plage spécifiée.
■ LIGNES et COLONNES – renvoient respectivement le nombre de lignes et de colonnes dans une plage. Dans notre formule de corrélation, les deux sont utilisés dans un seul but : obtenir le nombre de colonnes à décaler par rapport à la plage de départ. Et ceci est réalisé en utilisant intelligemment des références absolues et relatives .
Pour mieux comprendre la logique, voyons comment la formule calcule les coefficients mis en évidence dans la capture d’écran ci-dessus.
Tout d’abord, examinons la formule en B18, qui trouve une corrélation entre la température mensuelle (B2 : B13) et les appareils de chauffage vendus (D2 : D13) :
=COEFFICIENT.CORRELATION(DECALER($B$2:$B$13; 0; LIGNES($1:3)-1); DECALER($B$2:$B$13; 0; COLONNES($A:A)-1))
Dans la première fonction DECALER, LIGNES($1:1) s’est transformé en LIGNES($1:3) car la deuxième coordonnée est relative, elle change donc en fonction de la position relative de la ligne où la formule est copiée (2 lignes vers le bas). Ainsi, LIGNES() renvoie 3, dont nous soustrayons 1, et obtenons une plage située 2 colonnes à droite de la plage source, c’est-à-dire $D$2:$D$13 (Radiateurs vendus).
Le deuxième DECALER( ) ne modifie pas la plage spécifiée $B$2:$B$13 (température) car COLONNES($A:A)-1 renvoie zéro.
En conséquence, notre longue formule se transforme en un simple COEFFICIENT.CORRELATION($D$2:$D$13 ; $B$2:$B$13) et renvoie exactement le coefficient que nous voulons.
La formule en C18 qui calcule un coefficient de corrélation pour le coût publicitaire (C2 : C13) et les ventes (D2 : D13) fonctionne de manière similaire :
= COEFFICIENT.CORRELATION(DECALER($B$2:$B$13; 0; LIGNES($1:3)-1); DECALER($B$2:$B$13; 0; COLONNES($A:B)-1))La première fonction DECALER( ) est absolument la même que celle décrite ci-dessus, renvoyant la plage de $D$2:$D$13 (Radiateurs vendus).
Dans le deuxième DECALER, COLONNES($A:A)-1 devient COLONNES($A:B)-1 car nous avons copié la colonne de formule 1 à droite. Par conséquent, DECALER obtient une plage située 1 colonne à droite de la plage source, c’est-à-dire $C$2:$C$13 (coût publicitaire).
7. Problèmes potentiels de corrélation dans Excel
La corrélation du moment de Pearson ne révèle qu’une relation linéaire entre les deux variables. Cela signifie que vos variables peuvent être fortement liées d’une autre manière, curviligne, et avoir toujours le coefficient de corrélation égal ou proche de zéro.
La corrélation de Pearson ne permet pas de distinguer les variables dépendantes et indépendantes. Par exemple, en utilisant la fonction COEFFICIENT.CORRELATION( ) pour trouver l’association entre une température mensuelle moyenne et le nombre d’appareils de RADIATEUR vendus, nous avons obtenu un coefficient de -0,97, ce qui indique une forte corrélation négative. Cependant, vous pouvez inverser les variables et obtenir le même résultat. Ainsi, quelqu’un peut conclure que des ventes plus élevées d’appareils de chauffage entraînent une baisse de la température, ce qui n’a évidemment aucun sens. Par conséquent, lors de l’exécution d’une analyse de corrélation dans Excel, soyez conscient des données que vous fournissez.
De plus, la corrélation de Pearson est très sensible aux valeurs aberrantes. Si vous avez un ou plusieurs points de données qui diffèrent considérablement du reste des données, vous pouvez obtenir une image déformée de la relation entre les variables. Dans ce cas, il serait sage d’utiliser la corrélation de rang Spearman à la place.
Voilà comment faire la corrélation dans Excel.
8. Mieux comprendre la corrélation
La corrélation est basée sur la covariance, qui est symbolisée par sxy:
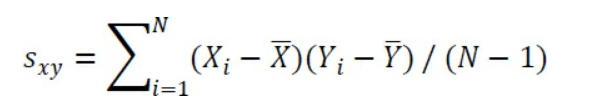
Cette formule peut vous sembler familière si vous avez lu la section sur la variance. Là, vous avez vu que la variance est calculée en soustrayant la moyenne de chaque valeur et en ajustant la déviation, c’est-à-dire multipliant la déviation par elle-même.
Notez que le dénominateur dans la formule de la covariance est N – 1. La raison est la même que pour la variance: Dans un échantillon, à partir de laquelle vous voulez faire des inférences sur une population, les degrés de liberté au lieu de N est utilisé pour rendre l’estimation indépendante de la taille de l’échantillon. Excel possède une fonction COVARIANCE.STANDARD ()à utiliser avec un ensemble de valeur que vous considérez comme un échantillon de valeurs et une fonction COVARIANCE.PEARSON () à utiliser avec un ensemble de valeurs que vous considérez comme une population.
Dans le même ordre d’idées, notez à partir de sa formule que la covariance d’une variable avec elle-même est simplement la variance de la variable.
Passer de la covariance à la corrélation
Même sans la fonction COEFFICIENT.CORRELATION() d’Excel, il est facile de passer de la covariance à la corrélation. La formule de définition du coefficient de corrélation entre la variable x et la variable y est la suivante: r = Sxy / SxSy
En termes de mots, la corrélation est égale à la covariance (Sxy)divisée par le produit de l’écart type de x (Sx)et de l’écart-type de y (Sy).La division supprime l’effet des écarts-types des deux variables de la mesure de leur relation. Prenant la propagation des deux variables hors de la corrélation fixe les limites du coefficient de corrélation à un minimum de -1,0 (corrélation négative parfaite), un maximum de +1,0 (corrélation positive parfaite) et un point médian de 0,0 (relation non observée) .
J’insiste sur les calculs de la covariance et du coefficient de corrélation car ils peuvent vous aider à comprendre la nature de ces deux statistiques. Lorsque des valeurs relativement grandes sur les deux variables vont de pair, la covariance est plus grande que dans le cas contraire. Une covariance plus grande entraîne un coefficient de corrélation plus élevé.
En pratique, vous ne réalisez presque jamais les calculs réels, mais laissez-les dans les fonctions de la feuille de calcul Excel COEFFICIENT.CORRELATION() pour le coefficient de corrélation et COVARIANCE.STANDARD ()ou COVARIANCE.PEARSON () pour la covariance.
Pourquoi Excel n’a-t-il pas les fonctions COEFFICIENT.CORRELATION. STANDARD ()et COEFFICIENT.CORRELATION.PEARSON ()? Supposons d’abord que vous avez affaire à une population de valeurs. Alors la formule pour r utiliserait N pour calculer la covariance de X avec Y. Il utiliserait également la racine carrée de N pour calculer les écarts-types de X et Y. Le dénominateur dans la formule pour r multiplie les deux écarts-types par l’autre, alors vous finissez par diviser N par N.
La situation est équivalente si vous travaillez avec un échantillon de valeurs, mais dans ce cas, vous finissez par diviser (N – 1) par (N – 1).
Plus succinctement, le résultat de l’expression
COVARIANCE.PEARSON (X, Y) / (ECARTYPE.PEARSON (X) * ECARTYPE.PEARSON (Y))
sera toujours égal au résultat de l’expression
COVARIANCE.STANDARD (X, Y) / (ECARTYPE.STANDARD (X) * ECARTYPE.STANDARD (Y))
