Calcul de la médiane avec Excel
La médiane d’un groupe d’observations est habituellement considérée comme l’observation moyenne quand ils sont dans l’ordre trié. Et c’est généralement un bon moyen d’y penser, même si c’est un peu imprécis. On dit souvent que la moitié
des observations se situent en dessous de la médiane alors que l’autre moitié
se trouve au-dessus. Supposons que vos observations soient composées des nombres 1, 2, 3, 4 et 5. Le nombre moyen de cet ensemble est 3. Mais il n’est pas vrai que la moitié des nombres se trouvent toujours au-dessus ou en dessous de la moyenne. Il est exact de dire que le même nombre d’observations se situe au-dessous de la médiane et l’autre en dessus. Dans l’exemple précédent, deux observations se situent en dessous de 3 et deux se trouvent au-dessus de 3.
S’il y a un nombre pair d’observations dans l’ensemble de données, il est juste de dire que la moitié se situe en dessous de la médiane et la moitié au-dessus. Mais avec un nombre pair d’observations, il n’y a pas d’enregistrement intermédiaire spécifique et, par conséquent, il n’y a pas d’enregistrement médian identifiable. Ajouter une observation à l’ensemble précédent, de sorte qu’il se compose de 1, 2, 3, 4, 5 et 6. Il n’y a pas d’enregistrement au milieu de cet ensemble ou aussi 1, 2, 3, 3, 3 et 4. Bien que l’un des 3 soit la médiane, il n’y a pas d’enregistrement spécifique et identifiable au milieu de l’ensemble.
Une façon utilisée par Excel pour calculer la médiane avec un nombre pair d’enregistrements est de prendre la moyenne des deux nombres moyens. Dans cet exemple, la moyenne de 3 et 4 est de 3,5, ce que Excel calcule comme la médiane de 1, 2, 3, 4, 5 et 6. Et puis, avec un nombre pair d’observations, exactement la moitié des observations se situent en dessous et la moitié au-dessus de la médiane. Mais 3.5 n’est pas un élément de l’ensemble.
Remarque
D’autres façons de calculer la médiane sont disponibles lorsqu’il existe des valeurs liées ou un nombre pair de valeurs : Une méthode est l’interpolation dans un groupe de valeurs liées. Mais la méthode utilisée par Excel a la vertu de la simplicité : c’est facile à calculer, à comprendre et à expliquer. Et vous ne vous tromperez pas si Excel calcule une valeur médiane de 65,5 lorsque l’interpolation vous aurait donné 65,7.
La syntaxe de la fonction MEDIANE () renvoie la syntaxe de la fonction MOYENNE (). Pour les données présentées dans la figure 2.7, il vous suffit d’entrer cette formule :
= MEDIANE (A2: A61)
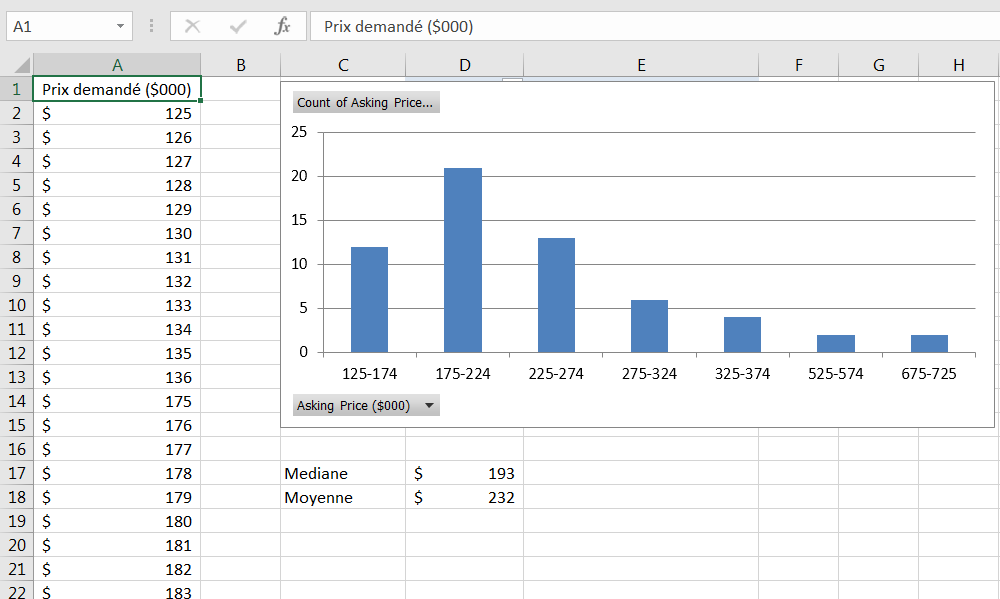
Figure 2.7. La moyenne et la médiane sont différentes dans les distributions asymétriques.
Choisir d’utiliser la médiane
La médiane est parfois une mesure plus descriptive de la tendance centrale que la moyenne. Par exemple, la figure 2.7 montre ce qu’on appelle une distribution asymétrique. La plupart des valeurs se regroupent sur le côté gauche, et quelques-unes sont situées à droite (bien sûr, une distribution peut biaiser dans n’importe quelle direction – celle-ci est faussée à droite). Ce type de distribution est typique des prix des maisons et c’est la raison pour laquelle l’industrie de l’immobilier rapporte des médianes au lieu des moyennes.
À la figure 2.7, notez que le prix médian des maisons déclaré est de 193 000 $ et que le prix moyen des maisons est 232 000 $. La médiane ne répond qu’au nombre d’observations classées, mais la moyenne répond également à la taille des valeurs des observations.
Supposons qu’au cours d’une semaine le prix de la maison la plus chère augmente de
100 000 $ et il n’y a pas d’autres changements dans les prix du logement. La médiane demeure où elle était, car elle se situe toujours au 50e percentile de la distribution des prix des maisons. C’est ce classement de 50% qui compte, pas les dollars associés à la maison la plus chère – ou, d’ailleurs, la moins chère.
En revanche, la moyenne réagirait si la maison la plus chère augmentait en prix. Dans la situation illustrée à la figure 2.7, une augmentation de 120 000 $ du prix d’une seule maison augmenterait la moyenne de 2 000 $, mais la médiane demeurerait telle qu’elle est.
La qualité relativement statique de la médiane est l’une des raisons pour lesquelles c’est la mesure préférée de la tendance centrale pour les prix du logement et des données similaires. Une autre raison est que lorsque les distributions sont faussées, la médiane peut fournir une meilleure mesure de la façon dont les choses ont une tendance centrale. Jetez un autre coup d’œil à la figure 2.7. Quelle statistique vous semble représenter le mieux le prix moyen de la maison?
chiffre: la moyenne de 232 000 $ ou la médiane de 193 000 $? C’est un jugement subjectif, bien sûr, mais beaucoup de gens jugeraient que 193 000 $ est un meilleur résumé des prix de ces maisons que 232 000 $.
