La variance est l’un des outils les plus utiles de la théorie des probabilités et des statistiques. En science, il décrit à quel point chaque nombre de l’ensemble de données est éloigné de la moyenne. En pratique, cela montre souvent à quel point quelque chose change. Par exemple, la température près de l’équateur a moins de variance que dans d’autres zones climatiques. Dans cette section, nous analyserons différentes méthodes de calcul de la variance dans Excel.
1. Qu’est-ce que la variance ?
La variance est la mesure de la variabilité d’un ensemble de données qui indique dans quelle mesure différentes valeurs sont réparties.
Mathématiquement, il est défini comme la moyenne des écarts au carré par rapport à la moyenne.
Pour mieux comprendre ce que vous calculez réellement avec la variance, veuillez considérer cet exemple simple.
Supposons qu’il y ait 5 tigres dans votre zoo local qui ont 14, 10, 8, 6 et 2 ans.
Pour trouver la variance, suivez ces étapes simples :
- Calculez la moyenne (moyenne simple) des cinq nombres :
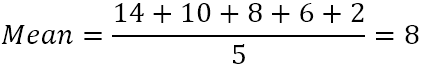
2.De chaque nombre, soustrayez la moyenne pour trouver les différences. Pour visualiser cela, traçons les différences sur le graphique :
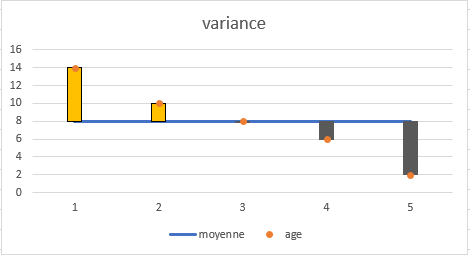
3.Mettez au carré chaque différence.
4.Calculez la moyenne des différences au carré.
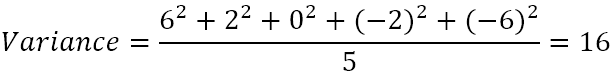
Donc, la variance est de 16. Mais que signifie réellement ce nombre ?
En vérité, la variance ne vous donne qu’une idée très générale de la dispersion de l’ensemble de données. Une valeur de 0 signifie qu’il n’y a pas de variabilité, c’est-à-dire que tous les nombres de l’ensemble de données sont identiques. Plus le nombre est grand, plus les données sont dispersées.
Cet exemple concerne la variance de la population (c’est-à-dire que 5 tigres représentent tout le groupe qui vous intéresse). Si vos données sont une sélection d’une population plus importante, vous devez calculer la variance de l’échantillon en utilisant une formule légèrement différente.
2. Comment calculer la variance dans Excel
Il existe 6 fonctions intégrées pour faire la variance dans Excel : VAR( ), VAR.S( ), VARP( ), VAR.P( ), VARA( ) et VARPA( ).
Votre choix de la formule de variance est déterminé par les facteurs suivants :
■La version d’Excel que vous utilisez.
■La variance de l’échantillon ou de la population.
■Vous souhaitez évaluer ou ignorer le texte et les valeurs logiques.
Le tableau ci-dessous donne un aperçu des fonctions de variation disponibles dans Excel pour vous aider à choisir la formule la mieux adaptée à vos besoins.
| Nom | Version Excel | Type de données | Texte et logique |
| VAR | 2000 – 2019 | Echantillon | Ignoré |
| VAR.S | 2010 – 2019 | Echantillon | Ignoré |
| VARA | 2000 – 2019 | Echantillon | Évalué |
| VARPE | 2000 – 2019 | Population | Ignoré |
| VAR.P | 2010 – 2019 | Population | Ignoré |
| VARPA | 2000 – 2019 | Population | Évalué |
3. VAR.S( ) contre VARA( ) et VAR.P( ) contre VARPA( )
VARA( ) et VARPA( ) ne diffèrent des autres fonctions de variance que par la manière dont elles gèrent les valeurs logiques et textuelles dans les références. Le tableau suivant fournit un résumé de la façon dont les représentations textuelles des nombres et des valeurs logiques sont évaluées.
| Type d’arguments | VAR( ), VAR.S( ), VAR.P( ), VAR.P.N( ) | VARA( ) & VARPA( ) |
| Valeurs logiques dans les tableaux et les références | Ignoré | Évalué (VRAI=1, FAUX=0) |
| Représentations textuelles de nombres dans des tableaux et des références | Ignoré | Evalué à zéro |
| Valeurs logiques et représentations textuelles des nombres saisis directement dans les arguments | Évalué (VRAI=1, FAUX=0) |
|
| Cellules vides | Ignoré | |
4. Comment calculer la variance de l’échantillon
Un échantillon est un ensemble de données extraites de l’ensemble de la population. Et la variance calculée à partir d’un échantillon est appelée variance d’échantillon .
Par exemple, si vous voulez savoir comment la taille des gens varie, il vous serait techniquement impossible de mesurer chaque personne sur la terre. La solution consiste à prendre un échantillon de la population, disons 1 000 personnes, et à estimer la taille de l’ensemble de la population sur la base de cet échantillon.
La variance de l’échantillon est calculée avec cette formule :
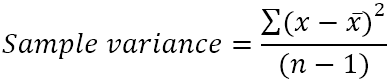
Où:
■ x̄est la moyenne (moyenne simple) des valeurs de l’échantillon.
■ n est la taille de l’échantillon, c’est-à-dire le nombre de valeurs dans l’échantillon.
Il existe 3 fonctions pour trouver la variance de l’échantillon dans Excel : VAR( ), VAR.S( ) et VARA( ).
Fonction VAR( ) dans Excel
C’est la plus ancienne fonction Excel pour estimer la variance sur la base d’un échantillon. La fonction VAR( ) est disponible dans toutes les versions d’Excel 2000 à 2019.
= VAR(nombre1 ; [nombre2] ; …)
Dans Excel 2010, la fonction VAR( ) a été remplacée par VAR.S( ) qui offre une précision améliorée. Bien que VAR( ) soit toujours disponible pour la rétrocompatibilité, il est recommandé d’utiliser VAR.S( ) dans les versions actuelles d’Excel.
Fonction VAR.S( ) dans Excel
C’est l’équivalent moderne de la fonction Excel VAR( ). Utilisez la fonction VAR.S( ) pour trouver la variance de l’échantillon dans Excel 2010 et versions ultérieures.
= VAR.S(nombre1, [nombre2], …)
Fonction VARA( ) dans Excel
La fonction Excel VARA( ) renvoie un échantillon de variance basé sur un ensemble de nombres, de texte et de valeurs logiques, comme indiqué dans le tableau précedent.
= VARA(valeur1 ; [valeur2] ; …)
Exemple de formule de variance
Lorsque vous travaillez avec un ensemble de données numériques, vous pouvez utiliser l’une des fonctions ci-dessus pour calculer la variance de l’échantillon dans Excel.
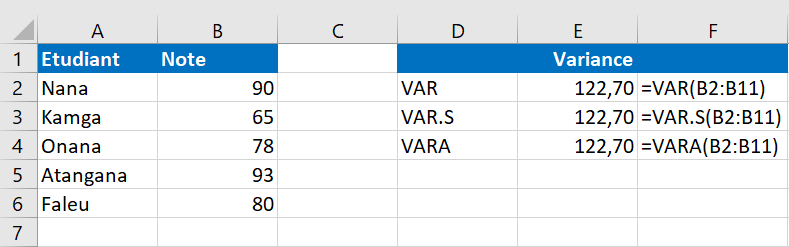
A titre d’exemple, trouvons la variance d’un échantillon composé de 5 éléments (B2:B6). Pour cela, vous pouvez utiliser l’une des formules ci-dessous :
=VAR(B2:B6)
=VAR.S(B2:B6)
=VARA(B2:B6)
Comme le montre la capture d’écran, toutes les formules renvoient le même résultat (arrondi à 2 décimales) :
Pour vérifier le résultat, effectuons le calcul de la variance manuellement :
- Trouvez la moyenne en utilisant la fonction MOYENNE :
=MOYENNE(B2:B6)
La moyenne va à n’importe quelle cellule vide, disons B7.
- Soustrayez la moyenne de chaque nombre de l’échantillon :
=B2-$B$7
Les différences vont à la colonne C, en commençant par C2.
- Mettez chaque différence au carré et placez les résultats dans la colonne D, en commençant par D2 :
=C2^2 - Additionnez les différences au carré et divisez le résultat par le nombre d’éléments dans l’échantillon moins 1 :
=SOMME(D2:D6)/(5-1)
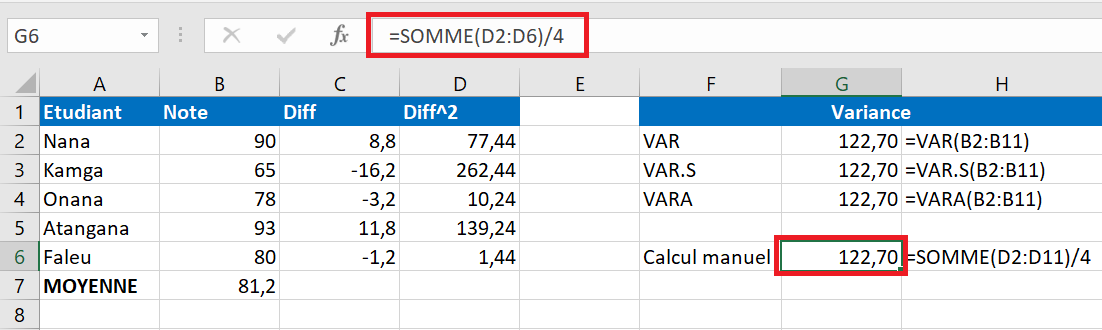
Comme vous pouvez le constater, le résultat de notre calcul manuel de la variance est exactement le même que le nombre renvoyé par les fonctions intégrées d’Excel :
Si votre ensemble de données contient les valeurs booléennes et/ou textuelles, la fonction VARA( ) renverra un résultat différent. La raison en est que VAR( ) et VAR.S( ) ignorent toutes les valeurs autres que les nombres dans les références, tandis que VARA( ) évalue les valeurs de texte comme des zéros, VRAI comme 1 et FAUX comme 0. Veuillez donc choisir avec soin la fonction de variance pour vos calculs selon que vous voulez traiter ou ignorer le texte et les logiques.
5. Comment calculer la variance de la population
La population est l’ensemble des membres d’un groupe donné, c’est-à-dire toutes les observations dans le domaine d’étude. La variance de la population décrit la répartition des points de données dans l’ensemble de la population.
La variance de la population peut être trouvée avec cette formule :
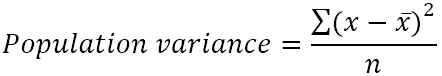
Où:
■ x̄est la moyenne de la population.
■ n est la taille de la population, c’est-à-dire le nombre total de valeurs dans la population.
Il existe 3 fonctions pour calculer la variance de la population dans Excel : VAR.P( ), VAR.P.N( ) et VARPA( ).
Fonction VAR.P( ) dans Excel
La fonction Excel VARP( ) renvoie la variance d’une population basée sur l’ensemble complet de nombres. Il est disponible dans toutes les versions d’Excel 2000 à 2019.
= VAR.P(nombre1 ; [nombre2] ; …)
Dans Excel 2010, VARP( ) a été remplacé par VAR.P( ) mais est toujours conservé pour la compatibilité descendante. Il est recommandé d’utiliser VAR.P( ) dans les versions actuelles d’Excel car il n’y a aucune garantie que la fonction VARP( ) sera disponible dans les futures versions d’Excel.
Fonction VAR.P.N( ) dans Excel
Il s’agit d’une version améliorée de la fonction VAR.P( ) disponible dans Excel 2010 et versions ultérieures.
VAR.P.N(nombre1 ; [nombre2] ; …)
Fonction VARPA( ) dans Excel
La fonction VARPA( ) calcule la variance d’une population en fonction de l’ensemble complet de nombres, de texte et de valeurs logiques. Il est disponible dans toutes les versions d’Excel 2000 à 2019.
VARPA(valeur1 ; [valeur2] ; …)
Formule de variance de population dans Excel
Dans l’exemple de calcul de la variance de l’échantillon, nous avons trouvé un écart de 5 notes d’examen en supposant que ces notes étaient une sélection d’un plus grand groupe d’étudiants. Si vous collectez des données sur tous les élèves du groupe, ces données représenteront l’ensemble de la population et vous calculerez une variance de population en utilisant les fonctions ci-dessus.
Disons que nous avons les notes d’examen d’un groupe de 10 étudiants (B2:B11). Les scores constituent l’ensemble de la population, nous allons donc faire la variance avec ces formules :
=VAR.P(B2:B11)
=VAR.P.N(B2:B11)
=VARPA(B2:B11)
Et toutes les formules retourneront le résultat identique :
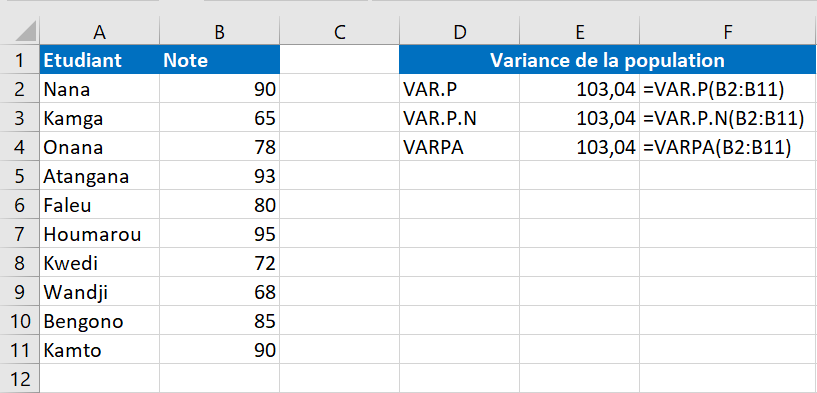
Pour vous assurer qu’Excel a correctement calculé la variance, vous pouvez la vérifier avec la formule de calcul manuel de la variable illustrée dans la capture d’écran ci-dessous :
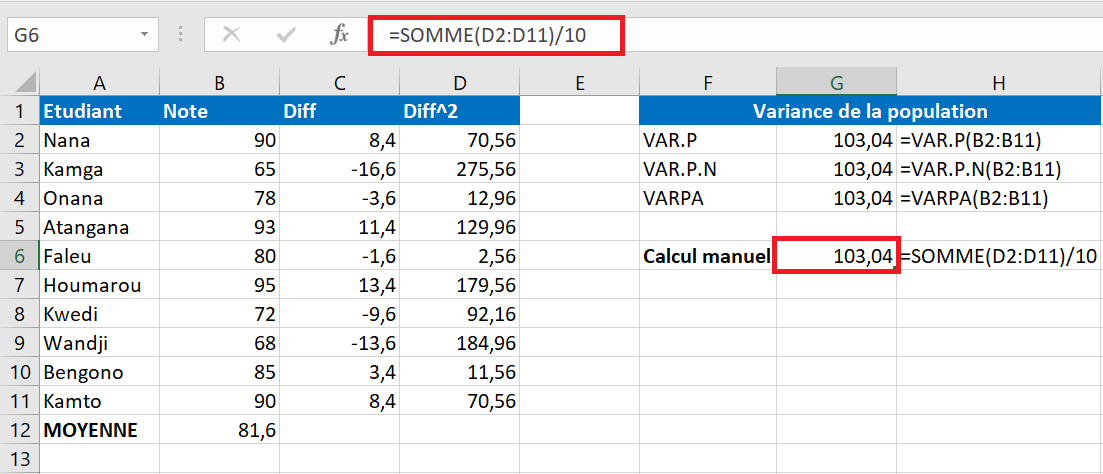
Si certains des étudiants n’ont pas passé l’examen et ont N/A au lieu d’une note, la fonction VARPA( ) renverra un résultat différent. La raison en est que VARPA( ) évalue les valeurs de texte comme des zéros tandis que VAR.P( ) et VAR.P.N( ) ignorent le texte et les valeurs logiques dans les références.
Formule de variance dans Excel – notes d’utilisation
Pour effectuer correctement l’analyse de la variance dans Excel, veuillez suivre ces règles simples :
■ Fournissez des arguments sous forme de valeurs, de tableaux ou de références de cellule.
■ Dans Excel 2007 et versions ultérieures, vous pouvez fournir jusqu’à 255 arguments correspondant à un échantillon ou à une population ; dans Excel 2003 et versions antérieures – jusqu’à 30 arguments.
■ Pour évaluer uniquement les nombres dans les références, en ignorant les cellules vides, le texte et les valeurs logiques, utilisez la fonction VAR( ) ou VAR.S( ) pour calculer la variance de l’échantillon et VAR.P( ) ou VAR.P.N( ) pour trouver la variance de la population.
■ Pour évaluer les valeurs logiques et textuelles dans les références, utilisez la fonction VARA( ) ou VARPA( ).
■ Fournissez au moins deux valeurs numériques à une formule de variance d’échantillon et au moins une valeur numérique à une formule de variance de population dans Excel, sinon un #DIV/0 ! erreur se produit.
■ Les arguments contenant du texte qui ne peut pas être interprété comme des nombres provoquent #VALUE ! les erreurs.
La variance est sans aucun doute un concept utile en science, mais il donne très peu d’informations pratiques. Par exemple, nous avons trouvé les âges de la population de tigres dans un zoo local et calculé la variance , qui est égale à 16. La question est : comment pouvons-nous réellement utiliser ce nombre ?
Vous pouvez utiliser la variance pour calculer l’écart type, qui est une bien meilleure mesure de la quantité de variation dans un ensemble de données.
L’écart type est calculé comme la racine carrée de la variance. Donc, nous prenons la racine carrée de 16 et obtenons l’écart type de 4.
En combinaison avec la moyenne, l’écart type peut vous indiquer l’âge de la plupart des tigres. Par exemple, si la moyenne est de 8 et l’écart type est de 4, la majorité des tigres du zoo ont entre 4 ans (8 – 4) et 12 ans (8 + 4).
