Excel ne vous fournit pas moins de six fonctions pour calculer l’écart-type d’un ensemble de valeurs, et il est assez facile d’obtenir l’écart-type sur une feuille de calcul. Si les valeurs qui vous intéressent se trouvent dans les cellules A2: A21,

vous pouvez entrer cette formule pour obtenir l’écart-type:
= ECARTYPEP(A2: A21)
(D’autres versions de la fonction sont abordées plus loin dans ce chapitre, dans la section intitulée «Fonctions de variabilité d’Excel».)
Le carré d’un écart type est appelé la variance. C’est une autre mesure importante du

variabilité dans un ensemble de valeurs. En outre, plusieurs fonctions dans Excel renvoient la variance d’un ensemble de valeurs. L’un est VAR.P (). Encore une fois, d’autres versions sont discutées plus tard dans «Fonctions de variabilité d’Excel». Vous entrez une formule qui utilise la fonction VAR.P () comme vous en entrez une qui utilise une fonction d’écart type: = VAR.P (A2: A21).
C’est tellement simple et facile, il ne semble pas raisonnable de prendre une formule quelque peu intimidante. Mais en regardant comment la statistique est définie aide souvent la compréhension.
Ainsi, bien que la majeure partie de ce chapitre concerne les écarts-types, il est important d’examiner de plus près la variance. Si, comme nos ancêtres, vous calculez des statistiques à la main, la variance est une station sur la route entre les données brutes et l’écart-type. Comprendre un aspect particulier de la variance facilite beaucoup la compréhension de l’écart-type.

Voici ce qu’on appelle souvent la formule définitionnelle de la variance:
 

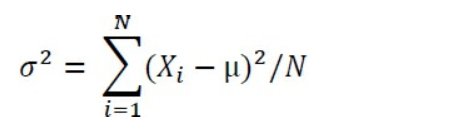
Remarque
Différentes formules ont des noms différents, même lorsqu’elles sont destinées à calculer la même quantité. Pendant de nombreuses années, les statisticiens ont évité d’utiliser la formule de définition que nous venons de montrer, car cela a conduit à des calculs maladroits, surtout lorsque les scores bruts n’étaient pas des nombres entiers. Des formules de calcul ont été utilisées à la place, et bien qu’elles aient eu tendance à obscurcir les aspects conceptuels d’une formule, elles ont rendu beaucoup plus facile de faire les calculs réels. Maintenant que nous utilisons des ordinateurs pour faire les calculs, nous avons besoin d’un ensemble différent d’algorithmes. Ces algorithmes sont destinés à améliorer la précision des calculs jusque dans les queues des distributions, où les nombres deviennent si petits que les méthodes de calcul traditionnelles donnent plus d’approximation que d’exactitude.

Voici la formule définitionnelle en mots:
Vous avez un ensemble de valeurs, où le nombre de valeurs est représenté par N. La lettre i est juste un identifiant qui vous indique l’une des valeurs N que vous utilisez lorsque vous travaillez dans les valeurs. Avec ces valeurs en main, la fonction d’écart-type d’Excel prend les mesures suivantes. Reportez-vous à la Figure 3.7 pour voir les étapes telles que vous pourriez les prendre dans une feuille de calcul, si vous vouliez traiter Excel comme l’équivalent du vingt et unième siècle d’une machine à additionner de Burroughs.
1. Calculer la moyenne des N valeurs. Dans la figure 3.7, la moyenne est montrée dans la cellule C2, en utilisant cette formule:
= MOYENNE (A2: A21)
2. Soustraire la moyenne de chacune des N valeurs (Xi). Ces différences (ou écarts) apparaissent dans les cellules E2: E21 de la figure 3.7.
3. Place chaque déviation. Voir les cellules G2: G21. La cellule G2 utilise cette formule :
= E2^2
4. Trouve le total des écarts quadratiques, montrés dans la cellule I2, en utilisant cette formule : SOMME (G2: G21)

5. 5. Divisez par N pour trouver l’écart quadratique moyen. Voir cellule K2, en utilisant cette formule: = I2 / 20
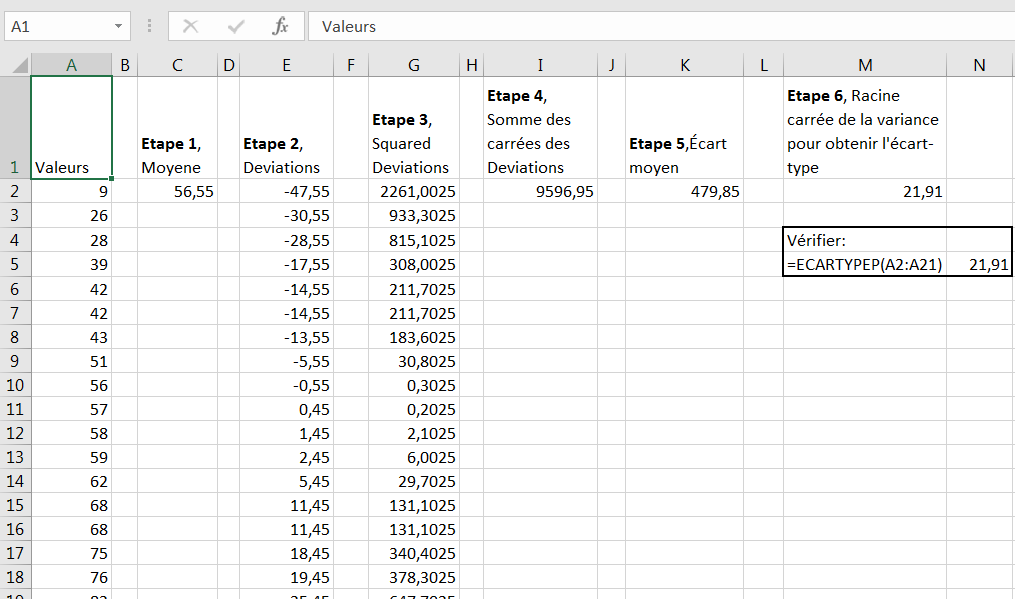
   Figure 3.7. Le long chemin vers la variance et l’écart-type.
    L’étape 5 entraîne la variance. Si vous réfléchissez à ces étapes, vous verrez que la variance est l’écart moyen au carré par rapport à la moyenne. Comme nous l’avons déjà vu, cette quantité n’a pas de sens intuitif. Vous ne dites pas, par exemple, que la mesure du LDL de John est une variance supérieure à la moyenne. Mais la variance est une statistique importante et puissante, et vous constaterez que vous vous sentez plus à l’aise en y réfléchissant à mesure que vous progressez dans les chapitres suivants de ce cours.
   Si vous vouliez faire un sixième pas en plus des cinq précédents, vous pourriez prendre la racine carrée de la variance. L’étape 6 donne l’écart-type, représenté par 21,91 dans la cellule M2 de la figure 1. La formule Excel est = RACINE (K2).
   À titre de vérification, vous trouverez la même valeur de 21,91 dans la cellule N5 de la figure 1. Il est beaucoup plus facile d’entrer la formule = ECARTYPEP (A2: A21) que de passer par toutes les manipulations dans les six étapes que l’on vient de donner. Néanmoins, il est utile de le faire une seule fois sur la feuille de travail, pour vous aider à apprendre et à conserver les concepts de quadrature, de sommation et de moyenne des écarts par rapport à la moyenne.

Remarque
Voir la section “Fonctions de variabilité d’Excel” plus loin dans ce chapitre pour une discussion de la différence entre ECARTYPE() et ECARTYPEP().
La figure 2 montre graphiquement la distribution de fréquence de la figure 1.

Figure 3.8. La distribution de fréquence se rapproche mais ne duplique pas une distribution normale.


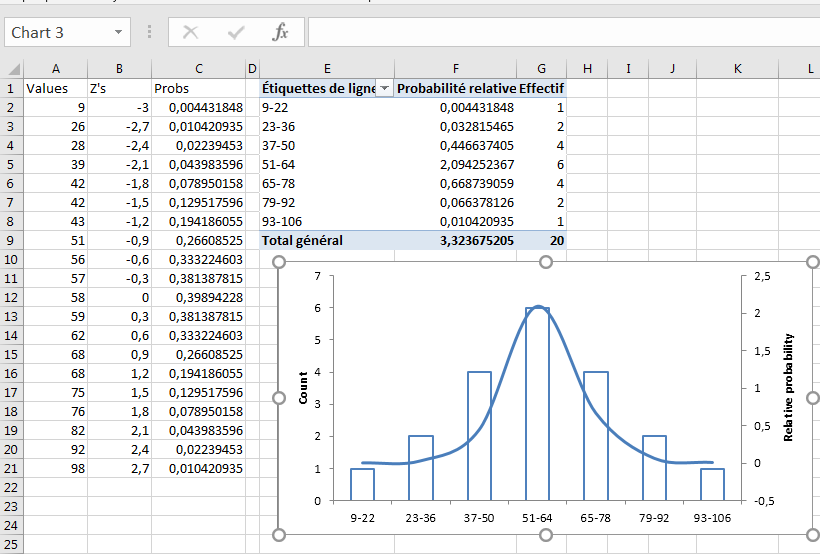
Notez dans la Figure 2 que les colonnes représentent le nombre d’enregistrements dans différents ensembles de valeurs. Une distribution normale est représentée par une courbe sur la figure. Les comptes indiquent clairement que cette distribution de fréquence est proche d’une distribution normale; cependant, en grande partie parce que le nombre d’observations est si petit, les fréquences s’écartent quelque peu des fréquences que la distribution normale vous ferait attendre.
Néanmoins, l’écart-type dans cette distribution de fréquence capture les valeurs dans les catégories qui sont à peu près équivalentes à la distribution normale.
Par exemple, la moyenne de la distribution est de 56,55 et l’écart type est de 21,91. Par conséquent, un score z de -1,0 (c’est-à-dire un écart-type inférieur à la moyenne) représente un score brut de 34,64. La figure 3.4 dit s’attendre à ce que 34% des observations se situent entre la moyenne et un écart-type de chaque côté de la moyenne.
Si vous examinez les scores bruts dans les cellules A2: A21 de la figure 3.7, vous verrez que six d’entre eux se situent entre 34,64 et 56,65. Six est 30% des 20 observations, et est une bonne approximation des 34% attendus. Ne dites jamais, mais vous voyez très rarement un petit échantillon tel que 20 enregistrements se conforment exactement à une distribution théorique. Plus l’échantillon est petit, plus l’effet potentiel de l’erreur d’échantillonnage est grand.

Équilibrer