Lorsque vous effectuez une analyse de corrélation dans Excel, dans la plupart des cas, vous traiterez la corrélation de Pearson. Mais comme le coefficient de corrélation de Pearson ne mesure qu’une relation linéaire entre deux variables, il ne fonctionne pas pour tous les types de données – vos variables peuvent être fortement associées de manière non linéaire et avoir toujours un coefficient proche de zéro. Dans de telles circonstances, vous pouvez faire la corrélation de rang de Spearman au lieu de celle de Pearson.

1 Corrélation de Spearman : les bases

La corrélation de Spearman est la version non paramétrique du coefficient de corrélation de Pearson qui mesure le degré d’association entre deux variables en fonction de leurs rangs.

La corrélation de Pearson teste la relation linéaire entre deux variables continues. Linéaire signifie une relation lorsque deux variables changent dans la même direction à un taux constant.

La corrélation de Spearman évalue la relation monotone entre les valeurs classées. Dans une relation monotone, les variables ont également tendance à changer ensemble, mais pas nécessairement à un rythme constant.

2 Quand faire la corrélation de Spearman

L’analyse de corrélation de Spearman doit être utilisée dans l’une des circonstances suivantes lorsque les hypothèses sous-jacentes de la corrélation de Pearson ne sont pas satisfaites :

1. Si vos données présentent une relation non linéaire ou ne sont pas normalement distribuées.
2. Si au moins une variable est ordinale. Si vos valeurs peuvent être placées dans l’ordre “premier, deuxième, troisième…”, vous avez affaire à des données ordinales.
3. S’il existe des valeurs aberrantes significatives. Contrairement à la corrélation de Pearson, la corrélation de Spearman n’est pas sensible aux valeurs aberrantes car elle effectue des calculs sur les rangs, de sorte que la différence entre les valeurs réelles n’a pas de sens.

Par exemple, vous pouvez utiliser la corrélation de Spearman pour trouver les réponses aux questions suivantes :

■ Les personnes plus scolarisées sont-elles plus soucieuses de l’environnement ?

■ Le nombre de symptômes d’un patient est-il lié à sa volonté de prendre des médicaments ?

3 Coefficient de corrélation de Spearman

En statistique, le coefficient de corrélation de Spearman est représenté soit par r _s soit par la lettre grecque ρ (“rho”), c’est pourquoi il est souvent appelé rho de Spearman.

Le coefficient de corrélation des rangs de Spearman mesure à la fois la force et la direction de la relation entre les rangs des données. Il peut s’agir de n’importe quelle valeur comprise entre -1 et 1, et plus la valeur absolue du coefficient est proche de 1, plus la relation est forte :

■ 1 est une corrélation positive parfaite

■ -1 est une corrélation négative parfaite

■ 0 n’est pas corrélé

4 Formule de corrélation de Spearman

Selon qu’il y a ou non des égalités dans le classement (le même rang attribué à deux observations ou plus), le coefficient de corrélation de Spearman peut être calculé avec l’une des formules suivantes.

S’il n’y a pas de rangs liés, une formule plus simple fera l’affaire :

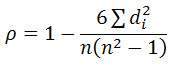
Où:

■ d_i est la différence entre une paire de rangs

■ n est le nombre d’observations

Pour traiter les rangs liés, la version complète de la formule de corrélation de Spearman doit être utilisée, qui est une version légèrement modifiée du r de Pearson :

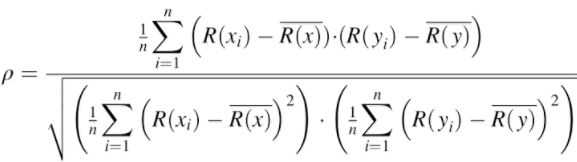
Où:

■ R(x) et R(y) sont les rangs des variables x et y

■ et sont les rangs moyens

5 Calculer la corrélation de Spearman dans Excel avec la fonction COEFFICIENT.CORRELATION

Malheureusement, Excel n’a pas de fonction intégrée pour calculer le coefficient de corrélation de Spearman. Cependant, cela ne signifie pas que vous devrez vous creuser la tête avec les formules ci-dessus. En manipulant un peu Excel, nous pouvons trouver un moyen beaucoup plus simple de faire la corrélation de Spearman.

A titre d’exemple, essayons de savoir si notre activité physique a un rapport avec notre tension artérielle. Dans la colonne B, nous avons le nombre de minutes que 10 hommes du même âge passent quotidiennement dans une salle de sport, et dans la colonne C, nous avons leur tension artérielle systolique.

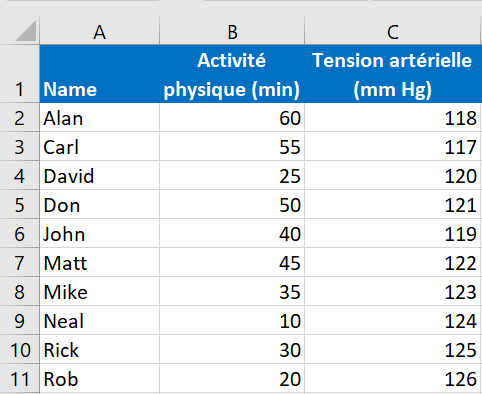
Pour trouver le coefficient de corrélation de Spearman dans Excel, procédez comme suit :

1. Classez vos données

Étant donné que la corrélation de Spearman évalue les associations entre deux variables en fonction de leurs classements, vous devez classer vos données source. Cela peut être fait rapidement en utilisant la fonction MOYENNE.RANG.

Pour classer la première variable (activité physique), saisissez la formule ci-dessous dans D2, puis faites-la glisser jusqu’à D11 :

=MOYENNE.RANG(B2;$B$2:$B$11;0)

Pour classer la deuxième variable (tension artérielle), mettez la formule suivante dans la cellule E2 et copiez-la dans la colonne :

=MOYENNE.RANG(C2;$C$2:$C$11;0)

Pour que les formules fonctionnent correctement, assurez-vous de verrouiller les plages avec des références de cellule absolues.

À ce stade, vos données sources devraient ressembler à ceci :

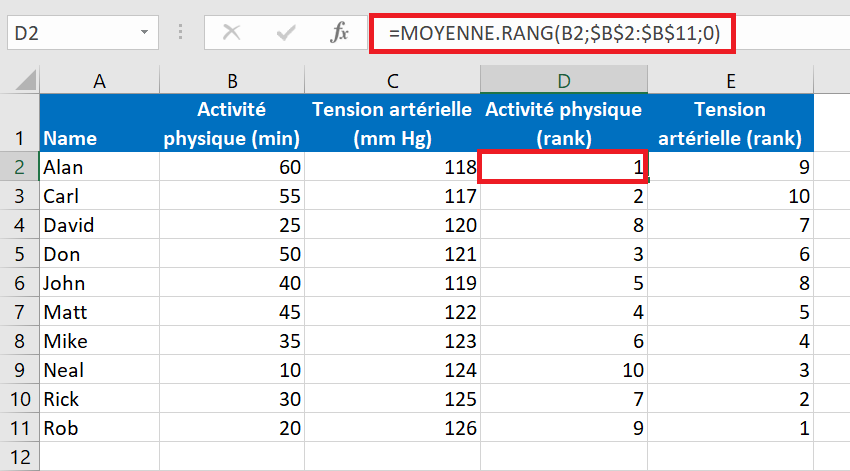
2. Trouver le coefficient de corrélation de Spearman

Une fois les classements établis, nous pouvons maintenant utiliser la fonction COEFFICIENT.CORRELATION pour obtenir le rho de Spearman :

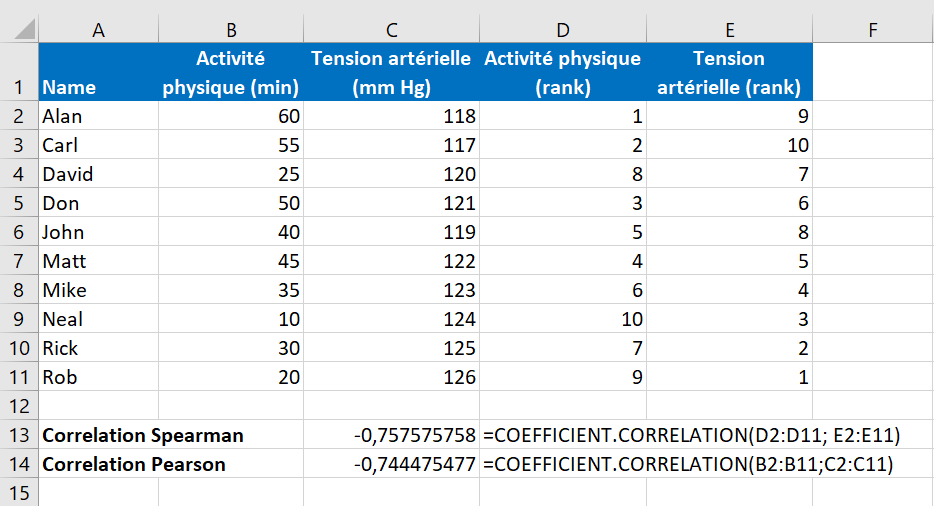
=COEFFICIENT.CORRELATION(D2:D11; E2:E11)

La formule renvoie un coefficient de -0,7576 (arrondi à 4 chiffres), ce qui montre une corrélation négative assez forte et permet de conclure que plus une personne fait de l’exercice, plus sa tension artérielle baisse.

Le coefficient de corrélation de Pearson pour le même échantillon (-0,7445) indique une corrélation un peu plus faible, mais toujours statistiquement significative :

La beauté de cette méthode est qu’elle est rapide, facile et fonctionne, qu’il y ait ou non des égalités dans le classement.

6 Calculer le coefficient de corrélation de Spearman dans Excel avec la formule traditionnelle

Si vous n’êtes pas tout à fait sûr que la fonction COEFFICIENT.CORRELATION  a calculé le rho de Spearman à droite, vous pouvez vérifier le résultat avec la formule traditionnelle utilisée dans les statistiques. Voici comment:

1. Trouvez la différence entre chaque paire de rangs ( d) en soustrayant un rang de l’autre :

=D2-E2

Cette formule va à F2 et est ensuite copiée dans la colonne.

2. Élevez chaque différence de rang à la puissance deux ( d ²):=F2^2

Cette formule va à la colonne G.

3. Additionnez les différences au carré :

=SOMME(G2:G11)

Cette formule peut aller dans n’importe quelle cellule vide, G12 dans notre cas. À partir de la capture d’écran suivante, vous comprendrez probablement mieux l’arrangement des données :

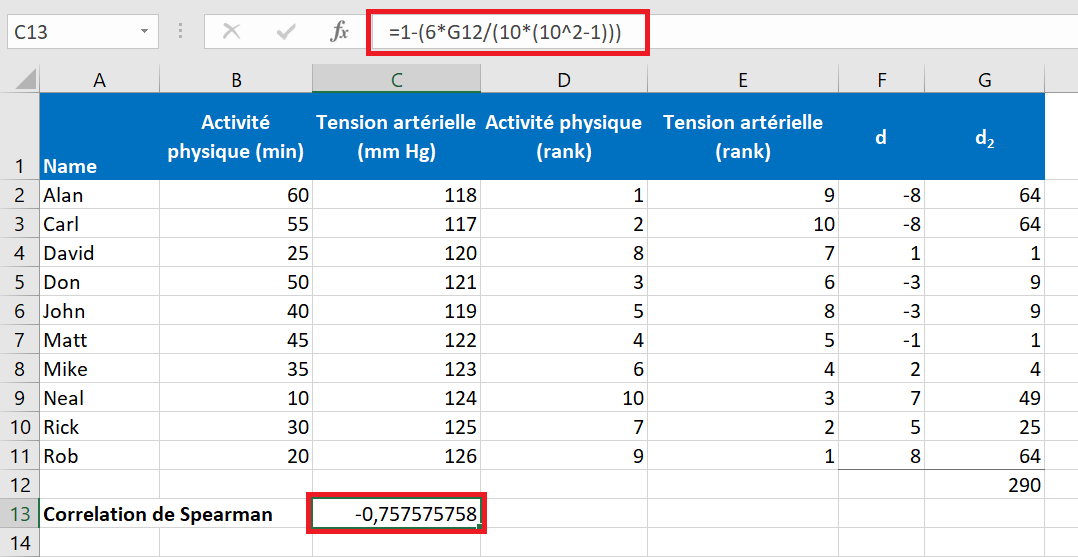
4. Selon que votre ensemble de données a des rangs liés ou non, utilisez l’une de ces formules pour calculer le coefficient de corrélation de Spearman.

Dans notre exemple, il n’y a pas de liens, nous pouvons donc utiliser une formule plus simple :

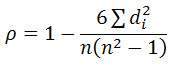
Avec d ² égal à 290, et n (nombre d’observations) égal à 10, la formule subit les transformations suivantes :

En conséquence, vous obtenez -0,757575758, ce qui correspond parfaitement au coefficient de corrélation de Spearman calculé dans l’exemple précédent.

Dans Microsoft Excel, les calculs ci-dessus peuvent être effectués avec l’équation suivante :

=1-(6*G12/(10*(10^2-1)))

Où G12 est la somme des différences de rang au carré (d ² ).