■■ Comment puis-je prédire les ventes automobiles trimestrielles aux États-Unis?

■■ Comment puis-je prédire les élections présidentielles américaines?

■■ Existe-t-il une fonction Excel que je peux utiliser pour faire facilement des prévisions à partir d’une équation de régression multiple?

Comment puis-je prédire les ventes d’automobiles trimestrielles aux États-Unis?

Supposons que vous souhaitiez prédire les ventes d’automobiles aux États-Unis pour déterminer si le trimestre de l’année affecte les ventes d’automobiles. Utilisez les données de la feuille de calcul Données du fichier , illustré à la figure 1. Les ventes sont répertoriées en milliers de voitures et le PNB est en milliards de dollars.

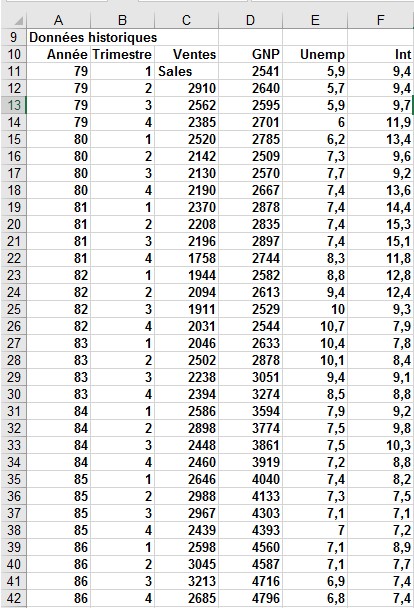
FIGURE 1 Voici les données des ventes automobiles.

Vous pourriez être tenté de définir une variable indépendante égale à 1 au cours du premier trimestre, 2 au cours du deuxième trimestre, etc. Malheureusement, cette approche forcerait le quatrième trimestre d’avoir quatre fois l’effet du premier trimestre, ce qui pourrait ne pas être vrai. Le trimestre de l’année est une variable indépendante qualitative. Pour modéliser une variable indépendante qualitative, vous créez une variable indépendante appelée variable fictive pour toutes les valeurs possibles de la variable qualitative sauf une. (Il est arbitraire quelle valeur vous omettez. Dans cet exemple, le quatrième trimestre a été omis.) Les variables muettes vous indiquent la valeur de la variable qualitative. Ainsi, vous disposez d’une variable fictive pour le trimestre 1, le trimestre 2 et le trimestre 3 avec les propriétés suivantes:

■■ La variable muette du trimestre 1 est égale à 1 si le trimestre correspond au trimestre 1 ou à 0 dans le cas contraire.

■■ La variable muette du deuxième trimestre est égale à 1 si le trimestre correspond au deuxième trimestre ou à 0 dans le cas contraire.

■■ La variable muette du trimestre 3 est égale à 1 si le trimestre correspond au trimestre 3 ou à 0 dans le cas contraire.

Une observation du quatrième trimestre sera identifiée par le fait que les variables muettes pour le trimestre 1 jusqu’au troisième trimestre égal à 0. Vous pouvez voir pourquoi vous n’avez pas besoin d’une variable fictive pour le quatrième trimestre. En fait, si vous incluez une variable fictive pour le quatrième trimestre en tant que variable indépendante dans la régression, Microsoft Excel renvoie un message d’erreur, car s’il existe une relation linéaire exacte entre tout ensemble de variables indépendantes, Excel doit effectuer l’équivalent mathématique de la division par 0 (une impossibilité)

lors de l’exécution d’une régression multiple. Dans cet exemple, si vous incluez une variable fictive Trimestre 4, chaque le point de données satisfait la relation linéaire exacte suivante:

(Mannequin 1 trimestre) + (Mannequin 2 trimestre) + (Mannequin 3 trimestre) + (Mannequin 4 trimestre) = 1

        Remarque :Une relation linéaire exacte se produit s’il existe des constantes c0, c1,. . . cN, tel que

pour chaque point de données, c0 + c1x1 + c2x2 +. . . cNxN = 0. Ici, x1 à xN sont les valeurs de

les variables indépendantes.

Pour créer la variable fictive pour le trimestre 1, copiez la formule IF (B12 = 1,1,0) de G12 à G13: G42. Cette formule place un 1 dans la colonne G chaque fois qu’un trimestre est le premier trimestre ou un 0 dans la colonne G chaque fois que le trimestre n’est pas le premier trimestre. De la même manière, créez des variables muettes pour le trimestre 2 (dans H12: H42) et le trimestre 3 (dans I12: I42). Vous pouvez voir les résultats des formules de la figure 2.

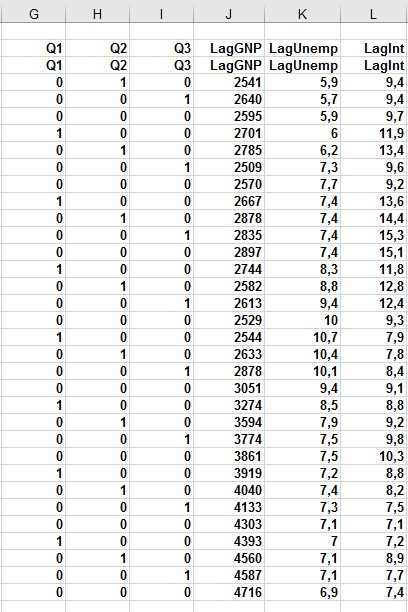
FIGURE 2 Utilisez des variables muettes pour suivre le trimestre au cours duquel une vente a lieu.

En plus de la saisonnalité, vous souhaitez utiliser des variables macroéconomiques telles que le produit national brut (PNB, en milliards de dollars de 1986), les taux d’intérêt et les taux de chômage pour prédire les ventes de voitures. Supposons, par exemple, que vous essayez d’estimer les ventes du deuxième trimestre de 1979. Étant donné que les valeurs du PNB, du taux d’intérêt et du taux de chômage ne sont pas connues au début du deuxième trimestre de 1979, vous ne pouvez pas utiliser le deuxième trimestre 1979 PNB, taux d’intérêt et taux de chômage pour prédire les ventes d’automobiles du deuxième trimestre 1979. Au lieu de cela, vous utilisez les valeurs du PNB, du taux d’intérêt et du taux de chômage décalés d’un trimestre pour prévoir les ventes d’automobiles. En copiant la formule = D11 de J12 à J12: L42, vous créer la valeur décalée pour le PNB, la première de vos variables indépendantes macroéconomiques. Par exemple, la fourchette J12: L12 contient le PNB, le taux de chômage et le taux d’intérêt pour le premier trimestre de 1979.

Vous pouvez maintenant exécuter la régression multiple en cliquant sur Analyse des données sous l’onglet Données et     fr en sélectionnant Régression dans la boîte de dialogue Analyse des données. Utilisez C11: C42 comme plage d’entrée Y et G11: L42 comme plage d’entrée X, sélectionnez l’option Étiquettes (la ligne 11 contient des étiquettes) et sélectionnez les résidus case à cocher. Après avoir cliqué sur OK, vous obtenez la sortie, que vous pouvez voir dans la feuille de calcul de régression et dans la figure 3, la figure 4 et la figure 5.

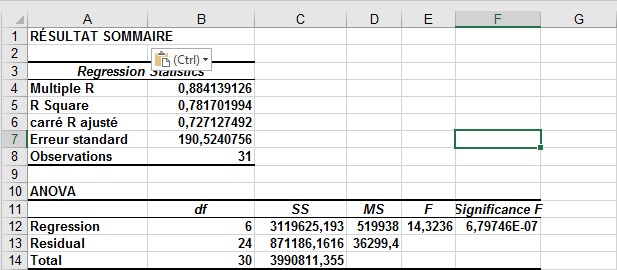
FIGURE 3 Il s’agit de la sortie récapitulative et du tableau ANOVA pour les données de ventes automobiles.

Dans la figure 4, vous pouvez voir que l’équation (équation 1) utilisée pour prédire les ventes d’automobiles trimestrielles est la suivante:

Ventes trimestrielles prévues = 3154,7 + 156,833T1 + 379,784T2 + 203,03 6T3 + .174 (LAGGNP en milliards) –93,83 (LAGUNEMP) –73,91 (LAGINT)

Toujours dans la figure 4, vous voyez que chaque variable indépendante a une valeur de p inférieure ou égale à 0,15. Vous pouvez conclure que toutes les variables indépendantes ont un effet significatif sur les ventes d’automobiles trimestrielles. Vous interprétez tous les coefficients d’une équation de régression ceteris paribus (ce qui signifie que chaque coefficient donne l’effet de la variable indépendante après ajustement pour les effets de toutes les autres variables de la régression).

FIGURE 4 Il s’agit des informations de coefficient pour la régression des ventes d’automobiles.

Voici une interprétation de chaque coefficient:

■■ Une augmentation de 1 milliard de dollars du PNB du dernier trimestre augmente les ventes trimestrielles de voitures de 174.

■■ Une augmentation de 1% du taux de chômage au dernier trimestre diminue les ventes trimestrielles de voitures de 93.832.

■■ Une augmentation de 1% du taux d’intérêt du dernier trimestre fait baisser les ventes trimestrielles de voitures de 73 917.

Pour interpréter les coefficients des variables muettes, vous devez comprendre qu’ils vous indiquent l’effet de la saisonnalité par rapport à la valeur laissée de côté par les variables qualitatives. Donc:

■■ Au premier trimestre, les ventes de voitures ont dépassé les ventes de voitures du quatrième trimestre de 156 833.

■■ Au deuxième trimestre, les ventes de voitures ont dépassé les ventes de voitures du quatrième trimestre de 379 784.

■■ Au troisième trimestre, les ventes de voitures ont dépassé les ventes de voitures du quatrième trimestre de 203 036.

Vous constatez que les ventes de voitures sont les plus élevées au deuxième trimestre (d’avril à juin; les remboursements de taxes et l’été arrivent) et les plus faibles au cours du troisième trimestre (d’octobre à décembre; pourquoi acheter une nouvelle voiture alors que le salage hivernal la ruine?).

À partir de la sortie récapitulative illustrée à la figure 58-3, vous pouvez apprendre les éléments suivants:

■■ La variation des variables indépendantes (facteurs macroéconomiques et saisonnalité) explique

78% de la variation de la variable dépendante (ventes trimestrielles de voitures).

■■ L’erreur standard de régression est de 190 524 voitures. Vous pouvez vous attendre à ce que 68% de vos prévisions soient exactes dans 190 524 voitures et 95% de vos prévisions dans 381 048 voitures (2 * 190 524).

■■ Trente et une observations sont utilisées pour ajuster la régression.

La seule quantité d’intérêt dans le tableau ANOVA de la figure 58-3 est la signification (0.00000068). Cette mesure implique qu’il n’y a que 6,8 chances sur 10 000 000 que, prises ensemble, toutes les variables indépendantes soient inutiles pour prévoir les ventes de voitures. Ainsi, vous pouvez être sûr que les variables indépendantes sont utiles pour prédire les ventes d’automobiles trimestrielles.

La figure 5 montre, pour chaque observation, les ventes prévues et résiduelles. Par exemple, pour le deuxième trimestre de 1979 (observation 1), les ventes prévues de l’équation 1 sont de 2 728,6, et le résidu est de 181 411 voitures (2910 – 2728,6). Notez qu’aucun résidu ne dépasse 381 000 en valeur absolue, vous n’avez donc pas de valeurs aberrantes.

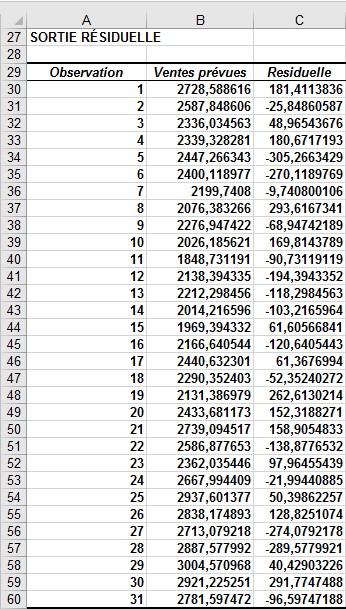
FIGURE 5 Ce sont les résidus pour les données de ventes d’automobiles.

Comment puis-je prédire les élections présidentielles américaines?

Lorsqu’on lui a demandé quels facteurs conduisaient les élections présidentielles, le conseiller présidentiel James Carville a déclaré: «C’est l’économie, stupide». L’économiste Roy Fair de Yale a montré que Carville avait raison de penser que l’État de l’économie a une grande influence sur les résultats des élections présidentielles. La variable dépendante de Fair (voir la fiche de données dans le fichier, illustré à la figure 6) pour chaque élection (1916 à 2012) était le pourcentage du vote bipartite (en ignorant les votes reçus par les candidats tiers) qui est allé à la partie en place. Il a essayé de prédire le pourcentage du parti sortant du vote bipartite en utilisant des variables indépendantes telles que:

■■ Parti au pouvoir Dans vos données, 1 indique quand le parti républicain était au pouvoir et 0 signifie quand le parti démocrate était au pouvoir.

■■ Croissance en pourcentage du PNB au cours des neuf premiers mois de l’année électorale

■■ Valeur absolue du taux d’inflation au cours des neuf premiers mois de l’élection

année Vous utilisez la valeur absolue car un taux d’inflation positif ou négatif est mauvais.

■■ Nombre de trimestres au cours des quatre dernières années au cours desquels la croissance économique a été forte Une croissance économique forte est définie comme une croissance annuelle de 3,2% ou plus.

■■ Durée pendant laquelle un parti sortant a été en fonction Fair Utilisé 0 pour désigner un mandat en fonction, 1 pour deux mandats, 1,25 pour trois mandats, 1,5 pour quatre mandats et 1,75 pour cinq mandats ou plus. Cette définition implique que chaque   m mandat après le premier mandat a moins d’influence sur les résultats des élections que le premier mandat.

■■ Élections en temps de guerre Les élections de 1920 (Première Guerre mondiale), 1944 (Seconde Guerre mondiale) et 1948 (la Seconde Guerre mondiale était toujours en cours en 1945) a été définie comme des élections en temps de guerre. (Les élections tenues pendant la guerre du Vietnam n’étaient pas considérées comme des élections en temps de guerre.) Pendant les années de guerre, les variables liées aux trimestres de bonne croissance et d’inflation ont été jugées non pertinentes et ont été fixées à 0.

■■ Le président actuel en lice pour la réélection Si tel est le cas, cette variable est définie sur 1; sinon, cette variable est fixée à 0. En 1976, Gerald Ford n’était pas considéré comme un président candidat à la réélection parce qu’il n’était élu ni comme président ni comme vice-président.

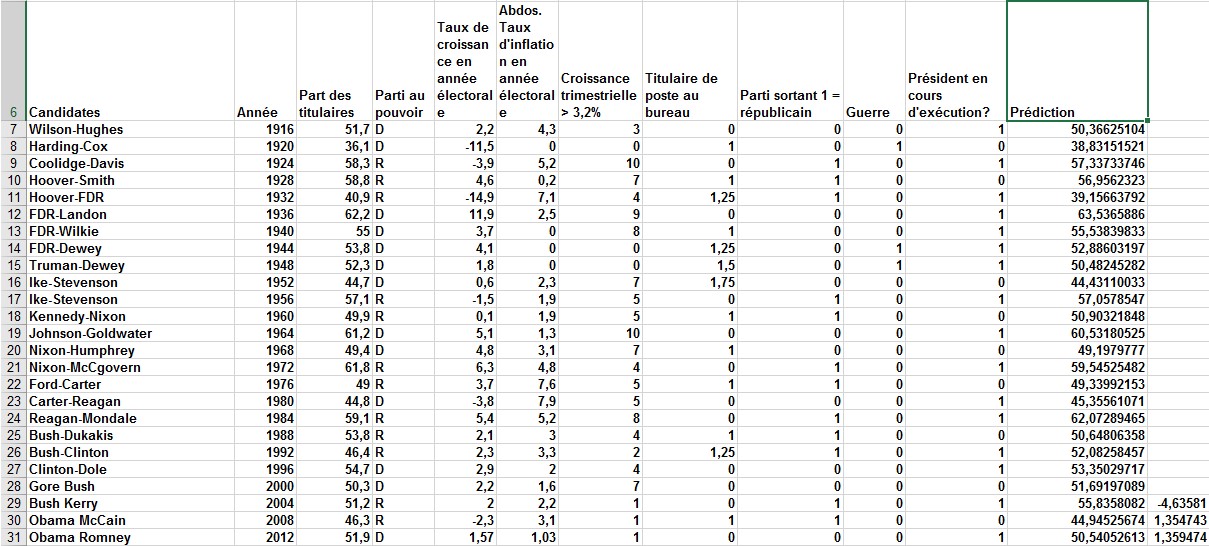
FIGURE 6 Il s’agit des données de l’élection présidentielle.

Les données des élections de 1916 à 2000 sont maintenant utilisées pour développer une équation de régression multiple qui peut être utilisée pour prévoir les futures élections présidentielles. Les élections de 2004, 2008 et 2012 ont été enregistrées comme points de validation. Lorsque vous ajustez une régression à des données, il est toujours judicieux de conserver certaines de vos données à utiliser pour valider votre équation de régression. La conservation des données vous permet de déterminer si votre équation de régression peut faire un bon travail de prévision des données

il n’a pas vu. Tout outil de prévision qui prévoit mal les données qu’il n’a pas vues ne doit pas être utilisé pour prédire l’avenir.

Pour exécuter la régression, cliquez sur Analyse des données dans le groupe Analyse sous l’onglet Données, puis sélectionnez l’outil de régression dans la boîte de dialogue Analyse des données. C7: C28 a été utilisé ici comme plage d’entrée Y et E7: L28 comme plage d’entrée X. L’option Étiquettes (la ligne 6 contient des étiquettes) a été sélectionnée. La sortie a été placée dans la feuille de calcul Réponse, que vous pouvez voir sur la Figure 7.

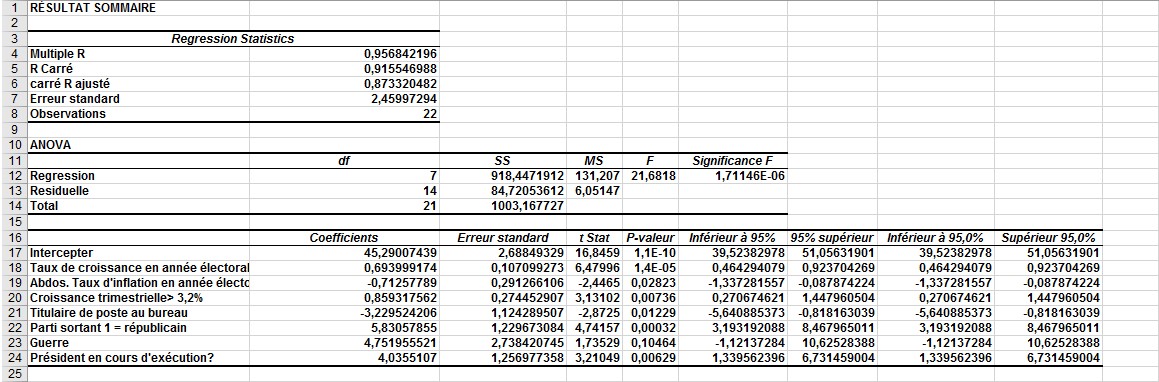
FIGURE 7 Il s’agit de la sortie de régression pour prédire les élections présidentielles.

Dans la figure 7, vous pouvez voir que toutes les variables indépendantes (si vous arrondissez le coefficient de guerre à 0,10) ont des valeurs de p inférieures ou égales à 0,10 et doivent toutes être utilisées dans les prévisions. À partir de la section des coefficients de la figure 58-7, vous pouvez déterminer que la meilleure équation pour prédire les élections est donnée par ce qui suit (équation 1):

Pourcentage prévu de l’élection présidentielle = 45,29 + 0,69 CROISSANCE – 0,71ABSINFL + 0,86 * QTRSGOODGROWTH- 3.23TIMEINOFFICE + 5.83REPB + 4.75WAR + 4.04PRESRUNNING

Les coefficients des variables indépendantes peuvent être interprétés comme suit (après ajustement pour toutes les autres variables indépendantes):

■■ Une augmentation de 1% du taux de croissance annuel du PNB pendant une année électorale vaut

0,69% à la partie en place.

■■ Un écart de 1% par rapport à l’idéal (0% d’inflation) coûte à l’opérateur historique

0,71% des voix.

■■ Chaque bon quart de croissance pendant le mandat d’une titulaire augmente son vote (peut-être un jour prochain) de 0,86%.

■■ Par rapport à un mandat, le deuxième mandat diminue le vote du titulaire

de 3,22%, et chaque mandat ultérieur diminue le vote du titulaire de 0,25 * (3,22%) =

0,80 pourcent.

■■ Un républicain a un avantage de 5,83% sur un démocrate.

■■ Les États-Unis en guerre ajoutent 4,79% à la prédiction de la part des voix des titulaires.

■■ Si le président est en fonction, vous devez ajouter 4,04% à votre prédiction pour la part de vote des titulaires.

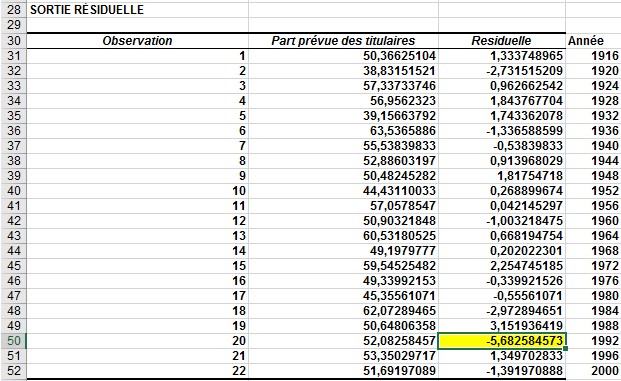
FIGURE 8 Ces chiffres sont des résidus de l’équation de l’élection présidentielle.

À partir de la cellule B5, vous voyez que votre régression explique 91,5% de la variation de la part des voix du titulaire. À partir de l’erreur standard de 2,46%, vous apprenez qu’environ 95% de vos prévisions devraient être exactes à 2 * 2,46 = 4,92%. Parce que la marge d’erreur sur les élections présidentielles le jour du scrutin est d’environ 3%, il est étonnant que votre modèle, qui ne tient pas compte de la qualité des candidats, s’en sort si bien! Regardez la figure 58-8; vous voyez que la seule valeur aberrante était la

Élection Bush – Clinton de 1992, au cours de laquelle Clinton a obtenu 5,68% de mieux que prévu. Cela pourrait être attribué au fait que Clinton était un grand militant.

Existe-t-il une fonction Excel que je peux utiliser pour faire facilement des prévisions à partir d’une équation de régression multiple?

Il est fastidieux de faire des prévisions à l’aide d’une équation telle que l’équation 1, mais la fonction Excel TENDANCE  facilite la génération de prévisions à partir d’une régression multiple. Vous n’avez même pas besoin d’exécuter une régression avec la commande Analyse des données . La syntaxe de la fonction TENDANCE est TENDANCE (Known_y’s, Known _x, New_x, Const). Cette fonction exécutera une régression qui tentera de prédire les y connus à partir des x connus. Les résultats de cette régression sont ensuite appliqués aux données du New x pour générer des prédictions basées sur  l’équation de régression ajustée. Si Const = TRUE, l’ordonnée à l’origine de régression est calculée normalement, tandis que si Const = FAUX, l’équation de régression est ajustée sans interception.

La fonction TENDANCE est un exemple de fonction de tableau. Une brève   introduction aux fonctions de tableau a été fourni dans l’article 57, «Introduction à la régression multiple», et une discussion plus complète des fonctions de tableau est proposée  dans l’article 87, «Formules et fonctions de tableau».

Pour illustrer l’utilisation de la fonction TENDANCE, la façon de générer des prévisions pour les élections de 1916 à 2012 est décrite en utilisant uniquement les données des élections de 1916 à 2000. Commencez, comme décrit au chapitre 57, en sélectionnant la plage de cellules (dans cet exemple, L17: L31) vers laquelle vous souhaitez que vos prévisions aillent. Avec le pointeur dans la première cellule de cette plage (cellule L17), entrez la formule = TENDANCE (C7: C28, E7: K28, E7: K31, Vrai). Ensuite, comme décrit au chapitre 57, appuyez sur Ctrl + Maj + Entrée. Vous voyez maintenant (voir la figure6) les prévisions pour chaque élection, générées dans les cellules L7: L31. Notons qu’en 2004, le président sortant (Bush) a réalisé 4,6% de moins que prévu et qu’en 2008 et 2012, les candidats du parti au pouvoir (McCain et Obama) ont obtenu 1,4% de mieux que prévu.