Vous devez souvent prévoir les valeurs futures d’une série chronologique, telles que les coûts mensuels ou les revenus mensuels des produits. Cela est généralement difficile car les caractéristiques de toute série chronologique changent constamment. Les méthodes de lissage ou d’adaptation sont généralement les mieux adaptées pour prévoir les valeurs futures d’une série chronologique. Ce chapitre décrit la méthode de lissage la plus puissante: la méthode de Winters. Pour vous aider à comprendre le fonctionnement de la méthode Winters, je vais l’utiliser pour prévoir les mises en chantier mensuelles aux États-Unis. Les mises en chantier sont simplement le nombre de nouvelles maisons dont la construction commence pendant un mois. Je vais commencer par décrire les trois caractéristiques clés d’une série chronologique.
Caractéristiques des séries chronologiques
Le comportement de la plupart des séries chronologiques s’explique par la compréhension de trois caractéristiques: la base, la tendance et la saisonnalité:
■■ La base d’une série décrit le niveau actuel de la série en l’absence de toute saisonnalité. Par exemple, supposons que le niveau de base pour les mises en chantier aux États-Unis soit 160 000. Dans ce cas, vous pouvez croire que si le mois en cours était un mois moyen par rapport aux autres mois de l’année, 160 000 mises en chantier se produiraient.
■■ La tendance d’une série chronologique est l’augmentation en pourcentage par période dans la base. Ainsi, une tendance
1.02 signifie que vous estimez que les mises en chantier augmentent de 2% chaque mois.
■■ La saisonnalité (indice saisonnier) d’une période vous indique dans quelle mesure au-dessus ou en dessous d’un mois typique vous pouvez vous attendre à ce que les mises en chantier soient. Par exemple, si l’indice saisonnier de décembre est de 0,8, les mises en chantier de décembre sont de 20% inférieures à un mois typique. Si l’indice saisonnier de juin est
1,3, puis les mises en chantier de juin sont 30 pour cent plus élevées qu’un mois typique.
Définitions des paramètres
Après avoir observé le mois t, vous aurez utilisé toutes les données observées jusqu’à la fin du mois t pour estimer les quantités d’intérêt suivantes:
■■= 
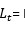Niveau de série
■■ 
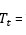= Tendance de la série
■■ 
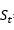= indice saisonnier pour le mois en cours
La clé de la méthode de Winters est les trois équations suivantes, qui sont utilisées pour mettre à jour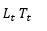 
et St. Dans les formules suivantes, alp, bet et gam sont appelés paramètres de lissage. Vous choisissez la valeurs de ces paramètres pour optimiser les prévisions. Dans les formules suivantes, c’est égal au nombre de périodes d’un cycle saisonnier (c = 12 mois, par exemple) et xt est égal à la valeur observée de la série chronologique au temps t:
■■ Formule 1 :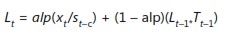
■■ Formule 2: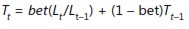
■■ Formule 3: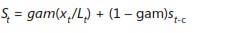
La formule 1 indique que la nouvelle estimation de base est une moyenne pondérée de l’observation actuelle (désaisonnalisée) et la base de la dernière période mise à jour par la dernière estimation de tendance. La formule 2 indique que la nouvelle estimation de tendance est une moyenne pondérée du rapport de la base actuelle à la base de la dernière période (il s’agit d’une estimation actuelle de la tendance) et de la tendance de la dernière période. La formule 3 indique que vous mettez à jour votre estimation de l’indice saisonnier en tant que moyenne pondérée de l’estimation de l’indice saisonnier en fonction de la période actuelle et de l’estimation précédente. Notez que des valeurs plus élevées des paramètres de lissage correspondent à donner plus de poids à l’observation actuelle.
Vous pouvez définir Ft, k comme votre prévision (F) après la période t pour la période t + k. Il en résulte la formule
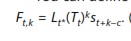. (J’appelle cela la formule 4.)
Cette formule utilise d’abord l’estimation de tendance actuelle pour mettre à jour les k périodes de base vers l’avant. Ensuite, l’estimation de base résultante pour la période t + k est ajustée par l’indice saisonnier approprié.
Initialisation de la méthode de Winters
Pour démarrer la méthode de Winters, vous devez avoir des estimations initiales pour les indices de base, de tendance et saisonniers de la série. Dans cet exemple, les mises en chantier mensuelles pour les années 1986 et 1987 ont été utilisées pour initialiser la méthode de Winters. Des paramètres de lissage ont ensuite été choisis pour optimiser les prévisions à un mois pour les années 1988 à 1996. Voir la figure 1 et le fichier . Voici les étapes qui ont été suivies.
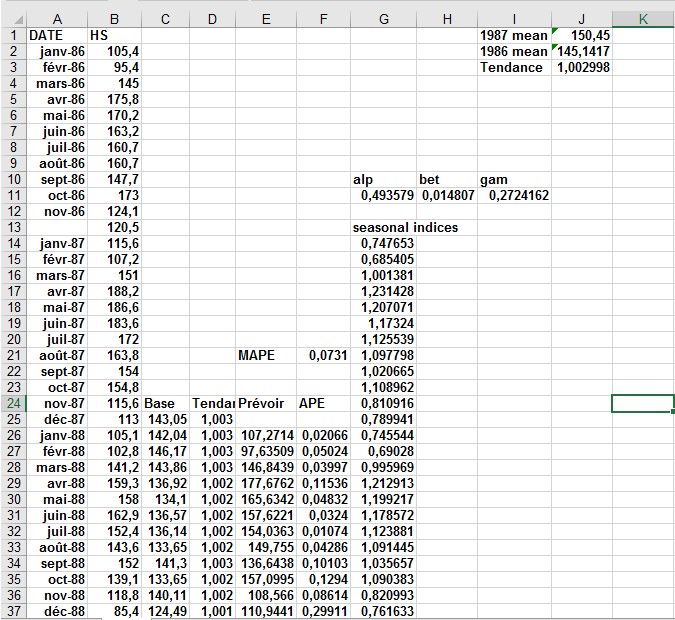
FIGURE 1 Initialisation de la méthode de Winters.
■■ Étape 1 Estimez, par exemple, l’indice saisonnier de janvier comme la moyenne des mises en chantier de janvier pour 1986 et 1987 divisée par les mises en chantier mensuelles moyennes pour 1986 et 1987. Par conséquent, la copie de = MOYENNE (B2, B14) / MOYENNE ($ B $ 2: $ B $ 25) formule du G14 au G15: G25 génère les estimations des indices saisonniers. Par exemple, l’estimation de janvier est de 0,75 et celle de juin de 1,17.
■■ Étape 2 Pour estimer la tendance mensuelle moyenne, divisez la douzième racine des mises en chantier moyennes de 1987 par les mises en chantier moyennes de 1986. Calculez cela dans la cellule J3 (et copiez-le dans la cellule D25) avec la formule= (J1 / J2) ^ (1/12) .
■■ Étape 3 À partir de janvier 1987, estimer la base de la série comme la désaisonnalisation
Valeur de décembre 1987. Cela a été calculé en C25 avec la formule = (B25 / G25).
Estimation des constantes de lissage
Vous êtes maintenant prêt à estimer les constantes de lissage. Dans la colonne C, vous pouvez mettre à jour base de série; dans la colonne D, la tendance des séries; et dans la colonne G, les indices saisonniers. Dans la colonne E, calculez les prévisions pour le mois suivant et, dans la colonne F, calculez le pourcentage absolu d’erreur pour chaque mois. Finalement, utilisez le solveur pour choisir des valeurs pour les constantes de lissage qui minimisent la somme des erreurs en pourcentage absolu. Voici le processus:
■■ Étape 1 Dans G11: I11, entrez des valeurs d’essai (entre 0 et 1) pour les constantes de lissage.
■■ Étape 2 Dans C26: C119, calculez le niveau de série mis à jour avec la formule 1 en copiant le
= alp * (B26 / G14) + (1 – alp) * (C25 * D25) formule de C26 à C27: C119.
■■ Étape 3 En D26: D119, utilisez la formule 2 pour mettre à jour la tendance de la série, en copiant le = bet * (C26/ C25) + (1 – pari) * Formule D25 de D26 à D27: D119.
■■ Étape 4 Dans G26: G119, utilisez la formule 3 pour mettre à jour les index saisonniers, en copiant le = gam * (B26/ C26) + (1 – gam) * Formule G14 de G26 à G27: G119.
■■ Étape 5 Dans E26: E119, utilisez la formule 4 pour calculer les prévisions pour le mois en cours en copiant la formule = (C25 * D25) * G14 de E26 à E27: E119.
■■ Étape 6 Dans F26: F119, calculez le pourcentage absolu d’erreur pour chaque mois en copiant le
= Formule ABS (B26-E26) / B26 de F26 à F27: F119.
■■ Étape 7 Calculez l’erreur moyenne absolue en pourcentage pour les années 1988 à 1996 dans F21 avec la formule = MOYENNE (F26: F119).
■■ Étape 8 Utilisez maintenant le solveur pour déterminer les valeurs des paramètres de lissage qui minimisent l’erreur moyenne absolue en pourcentage. La boîte de dialogue Paramètres du solveur est illustrée à la figure 2.
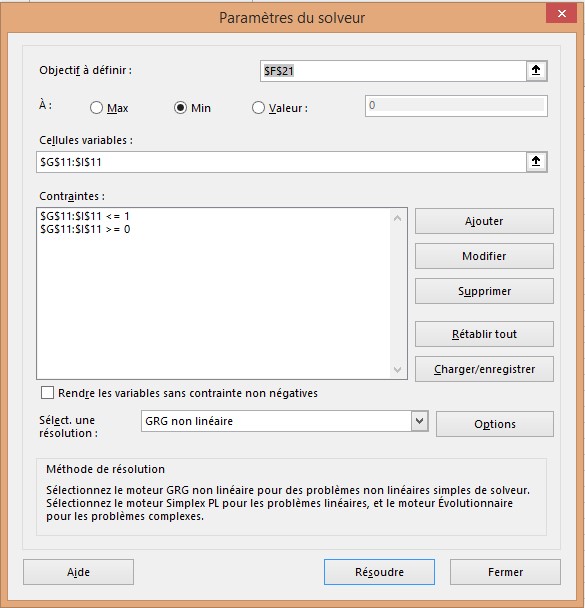
FIGURE 2 Boîte de dialogue Paramètres du solveur pour le modèle Winters.
Les paramètres de lissage (G11: I11) ont été utilisés pour minimiser l’erreur moyenne absolue en pourcentage (cellule F21). Le Solveur garantit que vous trouvez la meilleure combinaison de constantes de lissage. Les constantes de lissage doivent être comprises entre 0 et 1. Ici, alp = .50, bet = .01 et gam = .27 minimisent l’erreur de pourcentage absolu moyen. Vous pouvez trouver des valeurs légèrement différentes pour les constantes de lissage, mais vous devriez obtenir une erreur de pourcentage absolu moyen (MAPE) proche de 7,3%. Dans cet exemple, de nombreuses combinaisons des constantes de lissage donnent des prévisions ayant approximativement la même MAPE. Vos prévisions pour un mois à l’avance sont en baisse de 7,3% en moyenne.
Remarques
■■ Au lieu de choisir des paramètres de lissage pour optimiser les erreurs de prévision sur une période, vous pouvez, par exemple, choisir d’optimiser le pourcentage d’erreur absolue moyen encouru lors de la prévision du total des mises en chantier pour les six prochains mois.
■■ Si à la fin du mois t vous souhaitez prévoir les ventes pour les quatre prochains trimestres, vous devez simplement ajouter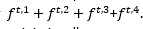
.Si vous le souhaitez, vous pouvez choisir des paramètres de lissage pour minimiser l’erreur en pourcentage absolu encourue lors de l’estimation des ventes pour l’année suivante.
Comment prévoir les valeurs futures d’une série chronologique Microsoft excel
Comment prévoir les valeurs futures d’une série chronologique Microsoft excel
Vous devez souvent prévoir les valeurs futures d’une série chronologique, telles que les coûts mensuels ou les revenus mensuels des produits. Cela est généralement difficile car les caractéristiques de toute série chronologique changent constamment. Les méthodes de lissage ou d’adaptation sont généralement les mieux adaptées pour prévoir les valeurs futures d’une série chronologique. Ce chapitre décrit la méthode de lissage la plus puissante: la méthode de Winters. Pour vous aider à comprendre le fonctionnement de la méthode Winters, je vais l’utiliser pour prévoir les mises en chantier mensuelles aux États-Unis. Les mises en chantier sont simplement le nombre de nouvelles maisons dont la construction commence pendant un mois. Je vais commencer par décrire les trois caractéristiques clés d’une série chronologique.
Caractéristiques des séries chronologiques
Le comportement de la plupart des séries chronologiques s’explique par la compréhension de trois caractéristiques: la base, la tendance et la saisonnalité:
■■ La base d’une série décrit le niveau actuel de la série en l’absence de toute saisonnalité. Par exemple, supposons que le niveau de base pour les mises en chantier aux États-Unis soit 160 000. Dans ce cas, vous pouvez croire que si le mois en cours était un mois moyen par rapport aux autres mois de l’année, 160 000 mises en chantier se produiraient.
■■ La tendance d’une série chronologique est l’augmentation en pourcentage par période dans la base. Ainsi, une tendance
1.02 signifie que vous estimez que les mises en chantier augmentent de 2% chaque mois.
■■ La saisonnalité (indice saisonnier) d’une période vous indique dans quelle mesure au-dessus ou en dessous d’un mois typique vous pouvez vous attendre à ce que les mises en chantier soient. Par exemple, si l’indice saisonnier de décembre est de 0,8, les mises en chantier de décembre sont de 20% inférieures à un mois typique. Si l’indice saisonnier de juin est
1,3, puis les mises en chantier de juin sont 30 pour cent plus élevées qu’un mois typique.
Définitions des paramètres
Après avoir observé le mois t, vous aurez utilisé toutes les données observées jusqu’à la fin du mois t pour estimer les quantités d’intérêt suivantes:
■■=
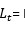Niveau de série
■■
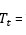= Tendance de la série
■■
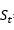= indice saisonnier pour le mois en cours
La clé de la méthode de Winters est les trois équations suivantes, qui sont utilisées pour mettre à jour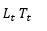
et St. Dans les formules suivantes, alp, bet et gam sont appelés paramètres de lissage. Vous choisissez la valeurs de ces paramètres pour optimiser les prévisions. Dans les formules suivantes, c’est égal au nombre de périodes d’un cycle saisonnier (c = 12 mois, par exemple) et xt est égal à la valeur observée de la série chronologique au temps t:
■■ Formule 1 :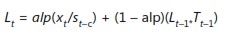
■■ Formule 2: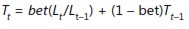
■■ Formule 3: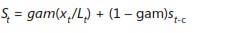
La formule 1 indique que la nouvelle estimation de base est une moyenne pondérée de l’observation actuelle (désaisonnalisée) et la base de la dernière période mise à jour par la dernière estimation de tendance. La formule 2 indique que la nouvelle estimation de tendance est une moyenne pondérée du rapport de la base actuelle à la base de la dernière période (il s’agit d’une estimation actuelle de la tendance) et de la tendance de la dernière période. La formule 3 indique que vous mettez à jour votre estimation de l’indice saisonnier en tant que moyenne pondérée de l’estimation de l’indice saisonnier en fonction de la période actuelle et de l’estimation précédente. Notez que des valeurs plus élevées des paramètres de lissage correspondent à donner plus de poids à l’observation actuelle.
Vous pouvez définir Ft, k comme votre prévision (F) après la période t pour la période t + k. Il en résulte la formule
Cette formule utilise d’abord l’estimation de tendance actuelle pour mettre à jour les k périodes de base vers l’avant. Ensuite, l’estimation de base résultante pour la période t + k est ajustée par l’indice saisonnier approprié.
Initialisation de la méthode de Winters
Pour démarrer la méthode de Winters, vous devez avoir des estimations initiales pour les indices de base, de tendance et saisonniers de la série. Dans cet exemple, les mises en chantier mensuelles pour les années 1986 et 1987 ont été utilisées pour initialiser la méthode de Winters. Des paramètres de lissage ont ensuite été choisis pour optimiser les prévisions à un mois pour les années 1988 à 1996. Voir la figure 1 et le fichier . Voici les étapes qui ont été suivies.
FIGURE 1 Initialisation de la méthode de Winters.
■■ Étape 1 Estimez, par exemple, l’indice saisonnier de janvier comme la moyenne des mises en chantier de janvier pour 1986 et 1987 divisée par les mises en chantier mensuelles moyennes pour 1986 et 1987. Par conséquent, la copie de = MOYENNE (B2, B14) / MOYENNE ($ B $ 2: $ B $ 25) formule du G14 au G15: G25 génère les estimations des indices saisonniers. Par exemple, l’estimation de janvier est de 0,75 et celle de juin de 1,17.
■■ Étape 2 Pour estimer la tendance mensuelle moyenne, divisez la douzième racine des mises en chantier moyennes de 1987 par les mises en chantier moyennes de 1986. Calculez cela dans la cellule J3 (et copiez-le dans la cellule D25) avec la formule= (J1 / J2) ^ (1/12) .
■■ Étape 3 À partir de janvier 1987, estimer la base de la série comme la désaisonnalisation
Valeur de décembre 1987. Cela a été calculé en C25 avec la formule = (B25 / G25).
Estimation des constantes de lissage
Vous êtes maintenant prêt à estimer les constantes de lissage. Dans la colonne C, vous pouvez mettre à jour base de série; dans la colonne D, la tendance des séries; et dans la colonne G, les indices saisonniers. Dans la colonne E, calculez les prévisions pour le mois suivant et, dans la colonne F, calculez le pourcentage absolu d’erreur pour chaque mois. Finalement, utilisez le solveur pour choisir des valeurs pour les constantes de lissage qui minimisent la somme des erreurs en pourcentage absolu. Voici le processus:
■■ Étape 1 Dans G11: I11, entrez des valeurs d’essai (entre 0 et 1) pour les constantes de lissage.
■■ Étape 2 Dans C26: C119, calculez le niveau de série mis à jour avec la formule 1 en copiant le
= alp * (B26 / G14) + (1 – alp) * (C25 * D25) formule de C26 à C27: C119.
■■ Étape 3 En D26: D119, utilisez la formule 2 pour mettre à jour la tendance de la série, en copiant le = bet * (C26/ C25) + (1 – pari) * Formule D25 de D26 à D27: D119.
■■ Étape 4 Dans G26: G119, utilisez la formule 3 pour mettre à jour les index saisonniers, en copiant le = gam * (B26/ C26) + (1 – gam) * Formule G14 de G26 à G27: G119.
■■ Étape 5 Dans E26: E119, utilisez la formule 4 pour calculer les prévisions pour le mois en cours en copiant la formule = (C25 * D25) * G14 de E26 à E27: E119.
■■ Étape 6 Dans F26: F119, calculez le pourcentage absolu d’erreur pour chaque mois en copiant le
= Formule ABS (B26-E26) / B26 de F26 à F27: F119.
■■ Étape 7 Calculez l’erreur moyenne absolue en pourcentage pour les années 1988 à 1996 dans F21 avec la formule = MOYENNE (F26: F119).
■■ Étape 8 Utilisez maintenant le solveur pour déterminer les valeurs des paramètres de lissage qui minimisent l’erreur moyenne absolue en pourcentage. La boîte de dialogue Paramètres du solveur est illustrée à la figure 2.
FIGURE 2 Boîte de dialogue Paramètres du solveur pour le modèle Winters.
Les paramètres de lissage (G11: I11) ont été utilisés pour minimiser l’erreur moyenne absolue en pourcentage (cellule F21). Le Solveur garantit que vous trouvez la meilleure combinaison de constantes de lissage. Les constantes de lissage doivent être comprises entre 0 et 1. Ici, alp = .50, bet = .01 et gam = .27 minimisent l’erreur de pourcentage absolu moyen. Vous pouvez trouver des valeurs légèrement différentes pour les constantes de lissage, mais vous devriez obtenir une erreur de pourcentage absolu moyen (MAPE) proche de 7,3%. Dans cet exemple, de nombreuses combinaisons des constantes de lissage donnent des prévisions ayant approximativement la même MAPE. Vos prévisions pour un mois à l’avance sont en baisse de 7,3% en moyenne.
Remarques
■■ Au lieu de choisir des paramètres de lissage pour optimiser les erreurs de prévision sur une période, vous pouvez, par exemple, choisir d’optimiser le pourcentage d’erreur absolue moyen encouru lors de la prévision du total des mises en chantier pour les six prochains mois.
■■ Si à la fin du mois t vous souhaitez prévoir les ventes pour les quatre prochains trimestres, vous devez simplement ajouter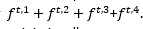
.Si vous le souhaitez, vous pouvez choisir des paramètres de lissage pour minimiser l’erreur en pourcentage absolu encourue lors de l’estimation des ventes pour l’année suivante.
Initiation à Excel
Fonctions Excel
Excel VBA
Macros VBA Utiles
Plus d'outils
Sur Facebook
Sur YouTube