En plus des graphiques qui affichent deux variables, telles que les nombres répartis par catégories dans un graphique à colonnes ou la relation entre deux variables numériques dans un graphique XY, il existe un autre type de

graphique Excel qui traite uniquement une variable. C’est la représentation visuelle d’une distribution de fréquences, un concept absolument fondamental pour les méthodes statistiques intermédiaires et avancées.
Une distribution de fréquence est destinée à montrer combien il y a d’instances de chaque valeur d’une variable. Par exemple:

• Le nombre de personnes pesant 100 livres, 101 livres, 102 livres, etc.

• Le nombre de voitures qui obtiennent 18 miles par gallon (mpg), 19 mpg, 20 mpg, et ainsi de suite

• Le nombre de maisons qui coûtent entre 200 001 $ et 205 000 $, entre 205 001 $ et
210 000 $, et ainsi de suite.
Parce que nous arrondissons généralement les mesures à un certain niveau de précision, une distribution de fréquence a tendance à regrouper des mesures individuelles en classes. En utilisant les exemples qui viennent d’être donnés, deux personnes pesant 100,2 et 100,4 livres peuvent chacune être classées comme 100 livres; deux voitures qui obtiennent 18,8 et 19,2 mpg pourraient être regroupées à 19 mpg; et n’importe quel nombre de maisons qui coûtent entre 220 001 $ et 225 000 $ serait traité comme étant au même niveau de prix.
Comme cela est généralement montré, le diagramme d’une distribution de fréquence place les valeurs de la variable sur son axe horizontal et le nombre d’instances sur l’axe vertical. La figure 1.10 montre une distribution de fréquence typique.

Figure 1.10. Généralement, la plupart des enregistrements se regroupent vers le centre d’une distribution de fréquence.

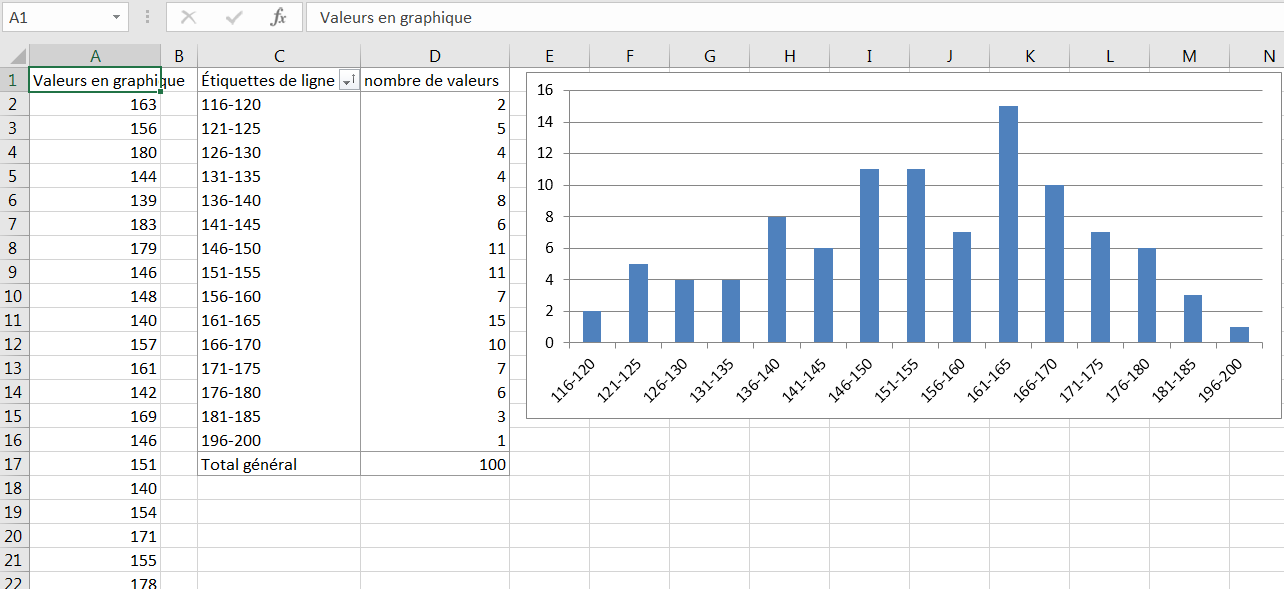
Vous pouvez en dire beaucoup sur une variable en regardant un graphique de sa distribution de fréquence. Par exemple, la figure 1.10 montre les poids d’un échantillon de 100 personnes. La plupart d’entre eux sont entre 140 et 180 . Dans cet échantillon, il y a environ autant de personnes qui pèsent beaucoup 175) comme il y en a dont le poids est relativement faible (disons, jusqu’à 130). L’étendu du poids c’est-à-dire, la différence entre les poids les plus légers et les plus lourds-est d’environ 85, de 116 à 200.

Il existe un large éventail de façons qu’un échantillon différent de personnes peut fournir des poids différents de ceux illustrés à la figure 1.10. Par exemple, la figure 1.11 montre un échantillon de 100 végétaliens. (Notez que la distribution de leurs poids est légèrement décalée vers le bas de l’échelle de l’échantillon de la population générale représentée à la figure 1.10.) 1

Figure 1.11. Par rapport à la figure 1.10, l’emplacement de la distribution de fréquence s’est décalé vers la gauche.

Les distributions de fréquence sur les figures 1.10 et 1.11 sont relativement symétriques. Leurs formes générales ne sont pas loin de la courbe “cloche” normale idéalisée, qui représente la distribution de nombreuses variables décrivant les êtres vivants. Ce cours a beaucoup plus à dire dans les chapitres suivants sur la courbe normale, en partie parce qu’il décrit autant de variables d’intérêt, mais aussi parce qu’Excel a tellement de façons de traiter la courbe normale.
Cependant, de nombreuses variables suivent une sorte différente de distribution de fréquence. Certains sont faussés à droite (voir Figure 1.12) et d’autres à gauche (voir Figure 1.13).

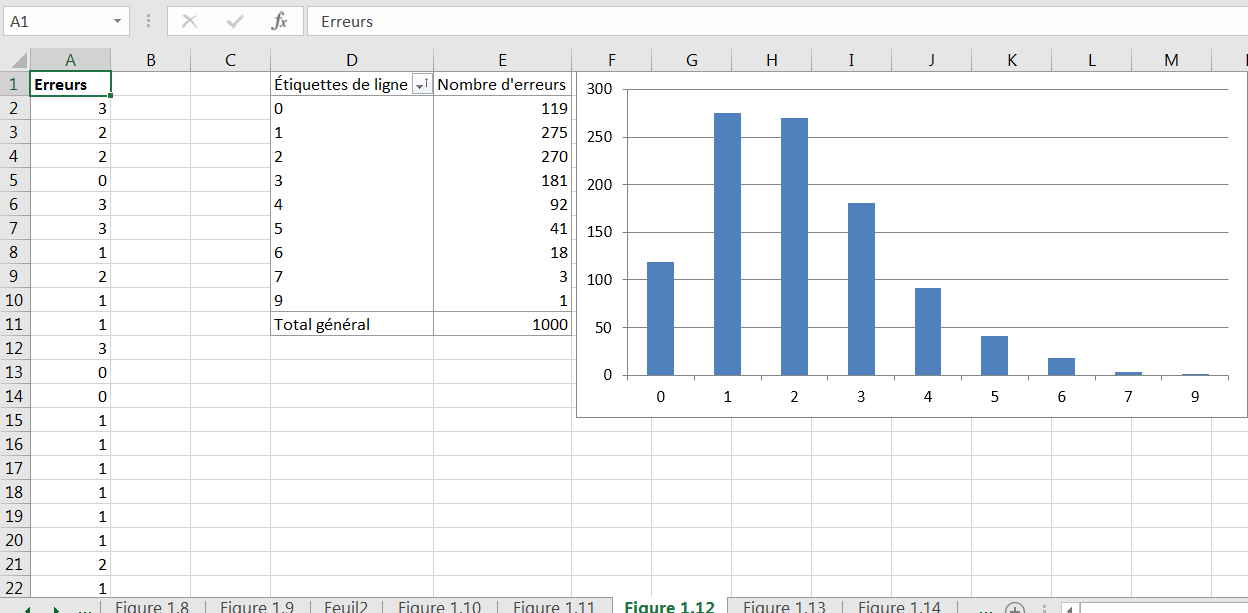
Figure 1.12. Une distribution de fréquence s’étendant vers la droite s’appelle positivement asymétrique.
 

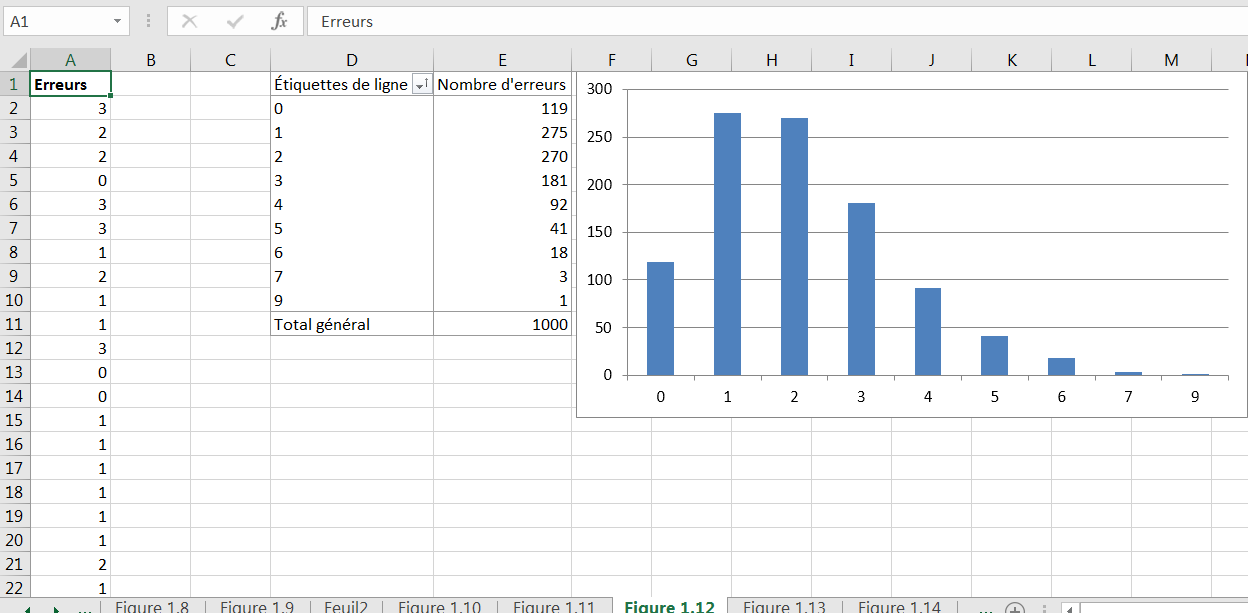
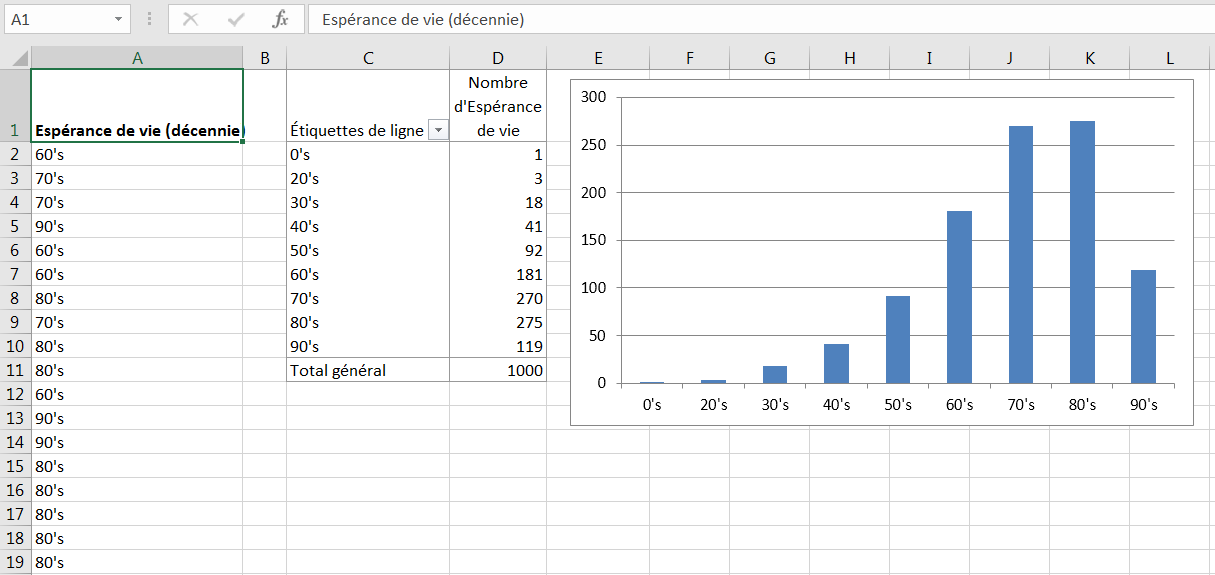
Figure 1.13. Les distributions biaisées négativement ne sont pas aussi courantes que les distributions asymétriquement positives.

La figure 1.12 montre le nombre d’erreurs sur les formulaires d’impôt fédéral individuels. Il est normal de faire quelques erreurs (disons une ou deux), et il est anormal de faire plusieurs (disons cinq ou plus). Cette distribution est positivement biaisée.
Une autre variable, les prix des maisons, ont tendance à être biaisée positivement, car bien qu’il y ait une limite inférieure réelle (une maison ne peut pas coûter moins de 0 $), il n’y a pas de limite supérieure théorique au prix d’une maison. Les prix des maisons ont donc tendance à grimper entre 100 000 $ et 300 000 $, avec moins entre 300 000 $ et 400 000 $, et encore moins à mesure que vous montez l’échelle.
Un ingénieur de contrôle de qualité peut échantillonner 100 carreaux de céramique à partir d’une production de 10 000 et compter le nombre de défauts sur chaque carreau. La plupart auraient zéro, un ou deux défauts; plusieurs en auraient trois ou quatre; et très peu en auraient cinq ou six. Ceci est une autre distribution positivement asymétrique – une situation plutôt courante dans le contrôle des processus de fabrication.
Parce que les vraies limites inférieures sont plus fréquentes que les vraies limites supérieures, vous avez tendance à rencontrer des distributions de fréquences plus faussées que positivement. Mais les biais négatifs se produisent certainement. La figure 1.13 pourrait représenter la longévité personnelle: Relativement peu de personnes meurent dans leur la vingtaine, la trentaine et la quarantaine, comparativement aux nombres qui meurent dans la cinquantaine jusqu’à la quarantaine.