Une distribution normale ou distribution gaussienne fait référence à une distribution de probabilité où les valeurs d’une variable aléatoire sont distribuées symétriquement. Ces valeurs sont également réparties à gauche et à droite de la tendance centrale. Ainsi, une courbe en forme de cloche se forme.

De plus, le nombre maximum de valeurs apparaît proche de la moyenne; la queue ne comprend que quelques valeurs. La règle empirique s’applique à de telles fonctions de probabilité. Par conséquent, 68 % des valeurs se situent dans une plage d’écart type. 95 % des observations se situent dans deux écarts types et 99,7 % des valeurs apparaissent dans trois écarts types.

1 Explication de la distribution normale

Une distribution normale ressemble à une disposition asymétrique de la plupart des valeurs autour de la moyenne, de telle sorte que la courbe ainsi formée ressemble à une cloche. Il comporte deux paramètres clés : la moyenne (µ) et l’écart type (σ). Cette méthode probabiliste joue un rôle crucial dans le calcul du rendement des actifs et les décisions stratégiques de gestion des risques. La figure suivante montre que la fonction de probabilité statistique est une courbe en forme de cloche qui suit la règle empirique :

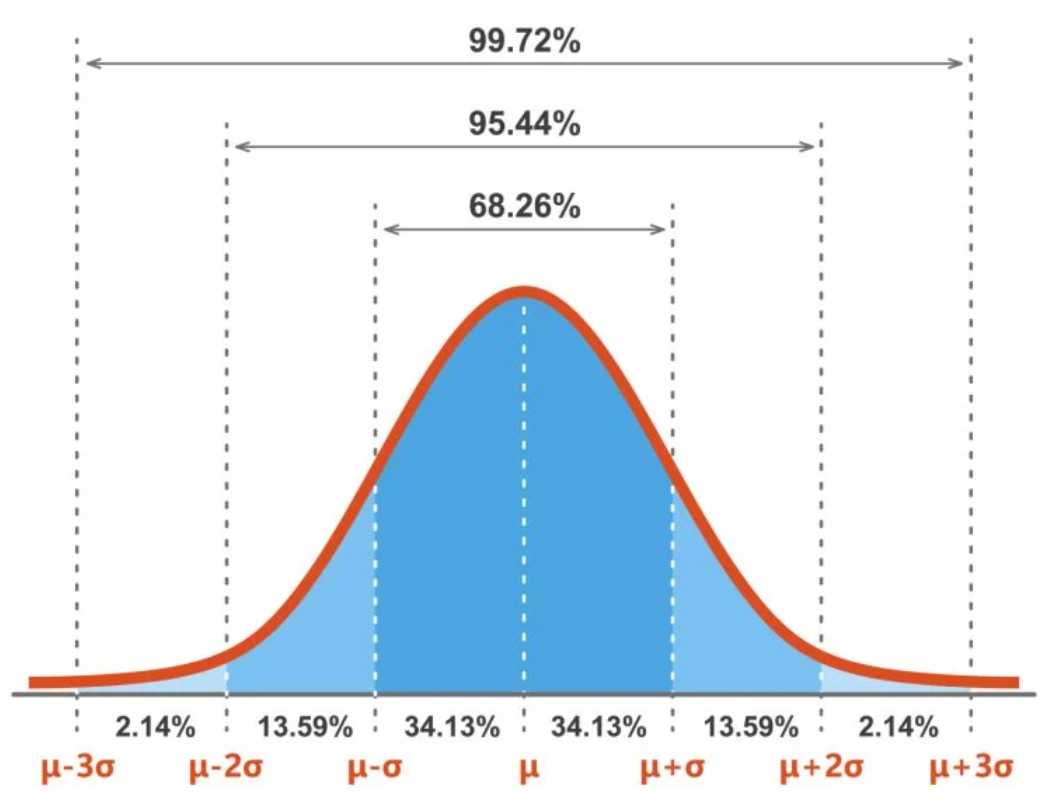
Les résultats possibles de la fonction sont donnés en termes de nombres réels entiers compris entre -∞ et +∞. Les queues de la courbe en cloche s’étendent des deux côtés du graphique (+/-) sans limites.

1. Environ 68 % de toutes les observations se situent dans une plage de +/- un écart type (σ).
2. Environ 95 % de toutes les observations se situent dans une plage de +/- deux écarts types (σ).
3. Près de 99,7 % de toutes les observations se situent dans une plage de +/- trois écarts types (σ).

L’asymétrie fait référence à la symétrie. Si L’asymétrie est 0, les données sont parfaitement symétriques. Si la distribution normale est inégale avec une asymétrie supérieure à zéro ou une asymétrie positive, alors sa queue droite sera plus prolongée que la gauche. De même, pour l’asymétrie négative, la queue gauche sera plus longue que la queue droite. Une asymétrie négative signifie que l’asymétrie est inférieure à zéro.

Aplatissement est une mesure de pointe. Si l’aplatissement est de 3, les données de probabilité ne sont ni trop pointues ni trop fines au niveau des queues. Si l’aplatissement est supérieur à trois, la courbe de données est alors accentuée avec des queues plus grosses. Alternativement, si l’aplatissement est inférieur à trois, alors les données représentées ont des queues fines avec le point culminant inférieur à la distribution normale. Pour une distribution normale, l’aplatissement est de 3.

Caractéristiques de la distribution normale

La distribution normale présente les caractéristiques suivantes qui la distinguent des autres formes de représentations probabilistes :

■ Règle empirique : Dans une distribution normale, 68% des observations sont confinées à -/+ un écart-type, 95% des valeurs se situent à -/+ deux écarts-types et près de 99,7% des valeurs sont confinées à -/+ trois. Écarts types.

■ Courbe en forme de cloche : la plupart des valeurs se trouvent au centre et moins de valeurs se trouvent aux extrémités de la queue. Il en résulte une courbe en forme de cloche.

■ Moyenne et écart type : cette représentation des données est façonnée par la moyenne et l’écart type.

■ Tendances centrales égales : la moyenne, la médiane et le mode de ces données sont égaux.

■ Symétrique : La courbe de distribution normale est à symétrie centrale. Par conséquent, la moitié des valeurs se trouvent à gauche du centre et les valeurs restantes apparaissent à droite. 

■ Asymétrie et Aplatissement : L’asymétrie est la symétrie. L’asymétrie d’une distribution normale est nulle. L’aplatissement étudie la queue des données représentées. Pour une distribution normale, l’aplatissement est de 3.

En résumé, pour savoir si une distribution est normale, les conditions suivantes sont remplies, alors les données représentées sont normales :
■ Courbe à symétrie centrale et en forme de cloche,
■ Moyenne, Médiane et Mode égaux,
■ La moyenne de la distribution est 0,
■ L’écart type est 1.
■ L’asymétrie est 0. .et
■ L’aplatissement est de 3.s

Cette fonction gaussienne est l’une des fonctions de densité de probabilité les plus populaires. En effet, il fournit efficacement les résultats ou probabilités proches des phénomènes naturels. Ainsi, il est universellement appliqué dans de nombreux domaines tels que l’économie, la finance, l’investissement, la psychologie, la science, la santé, les affaires et l’économie.

2 Formule de distribution normale

La fonction de densité de probabilité d’une variable aléatoire (X) est donnée par :

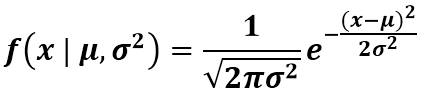
Où;

■ -∞ < x < ∞ ; -∞ < µ < ∞ ; σ > 0

■ F(x) = Fonction de probabilité normale

■ x = Variable aléatoire

■ µ = Moyenne de distribution

■ σ = écart type

■ de la répartition

■ π = 3,14159

■ e = 2,71828

Transformation (Z)

Lorsqu’il s’agit d’une étude comparative de deux échantillons ou plus, il devient nécessaire de convertir leurs valeurs en scores z. C’est ce qu’on appelle la transformation z.

Pour déterminer le z-score, la formule suivante est utilisée :

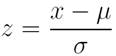
Où x = Variable aléatoire.

Tableau de distribution normale

Le tableau référencé pour l’écart type est le tableau z. Ici, nous déterminons la probabilité d’obtenir un résultat particulier à l’aide de la formule de transformation pour déterminer la valeur du score z, qui est représenté en pourcentage à l’aide d’un tableau z.

Exemple 1

Supposons qu’une entreprise compte 10 000 employés et plusieurs structures salariales selon des fonctions spécifiques. Les salaires sont généralement distribués avec la moyenne de µ = 60 000 $ et l’écart type de la population σ = 15 000 $. Quelle sera la probabilité qu’un employé sélectionné au hasard gagne moins de 45 000 $ par an ?

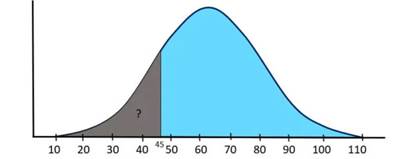
Solution :

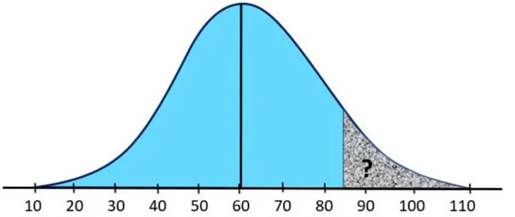
Comme le montre la figure ci-dessus, nous devons connaître l’aire sous la courbe normale de 45 jusqu’à la queue gauche pour répondre à cette question. De plus, nous devons utiliser la valeur de la table z pour obtenir la bonne réponse.

Premièrement, nous devons convertir la moyenne donnée et écart-type dans une distribution normale standard avec moyenne (µ) = 0 et écart type (σ) = 1 en utilisant la formule de transformation.

Après la conversion, nous devons rechercher la table z pour connaître la valeur correspondante, ce qui nous donnera la bonne réponse.

Donné,

■ Moyenne (µ) = 60 000 $

■ Écart type (σ) = 15 000 $

■ Variable aléatoire (x) = 45 000 $

Transformation (z) = (45 000 – 60 000 / 15 000)

Transformation (z) = -1

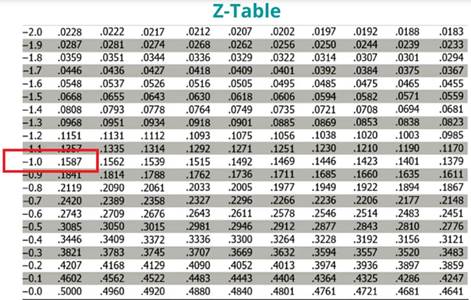
La valeur équivalente à -1 dans le tableau z est 0,1587, représentant l’aire sous la courbe de 45 vers la gauche. Ainsi, il indique que lorsque l’on sélectionne un employé au hasard, la probabilité de gagner moins de 45 000 $ par année est de 15,87 %.

Il est important de noter que nous avons converti la valeur du z-score 0,1587 en pourcentage en la multipliant par 100 pour obtenir 15,87 %.

Exemple n°2

Pour le même scénario ci-dessus, trouvez maintenant la probabilité qu’un employé sélectionné au hasard gagne plus de 85 000 $ par an.

Solution :

Donc, dans cette question, nous devons trouver la zone ombrée de 85 à la queue droite en utilisant la même formule.

Donné :

■ Moyenne (µ) = 60 000 $

■ Écart type (σ) = 15 000 $

■ Variable aléatoire (X) = 85 000 $

Transformation (z) = (85 000 – 60 000 /15 000)

Transformation (z) = 1,67

Selon le tableau Z, la valeur équivalente de 1,67 est 0,9525 ou 95,25 %, ce qui montre que la probabilité de sélectionner au hasard un employé gagnant moins de 85 000 $ par an est de 95,25 %.

Mais selon la question, nous devons déterminer la probabilité que des employés aléatoires gagnent plus de 85 000 $ par an, nous devons donc soustraire la valeur calculée de 100.

■ Variable aléatoire (X) = 100 % – 95,25 %

■ Variable aléatoire (X) = 4,75 %

Ainsi, la probabilité que les employés gagnent plus de 85 000 $ par an est de 4,75 %.

3 Distribution normale dans Excel

 La fonction de distribution normale est une fonction statistique intégrée d’Excel qui calcule la distribution normale d’un ensemble de données pour lequel la moyenne et l’écart type sont donnés.

La fonction LOI.NORMALE.N( ) accepte quatre arguments : valeur X, moyenne, écart type et valeur cumulée. Excel 2010 a remplacé la fonction LOI.NORMALE( ) par la fonction LOI.NORMALE.N( ).

Syntaxe :

Les arguments de la fonction LOI.NORMALE.N( )  sont répertoriés comme suit :

LOI.NORMALE.N(x ; espérance; écart_type;  cumulative)

La syntaxe de la fonction LOI.NORMALE.N contient les arguments suivants :

■ x Obligatoire. Représente la valeur dont vous recherchez la distribution.

■ moyenne Obligatoire. Représente la moyenne arithmétique de la distribution.

■ écart_type Obligatoire. Représente l’écart type de la distribution.

■ cumulative Obligatoire. Représente une valeur logique déterminant le mode de calcul de la fonction : cumulatif ou non. Si l’cumulative est VRAI, la valeur NORMALE. LA FONCTION.N renvoie la fonction de distribution cumulée. Si l’effet est FAUX, la fonction renvoie la fonction de densité de probabilité.

Exemple 1

Nous avons les données boursières d’une organisation. Le cours de l’action stipulé est de 115, le cours moyen global de l’action est de 90 et l’écart type est de 16.

Nous devons calculer la probabilité que le cours de l’action soit égal ou inférieur à 115.

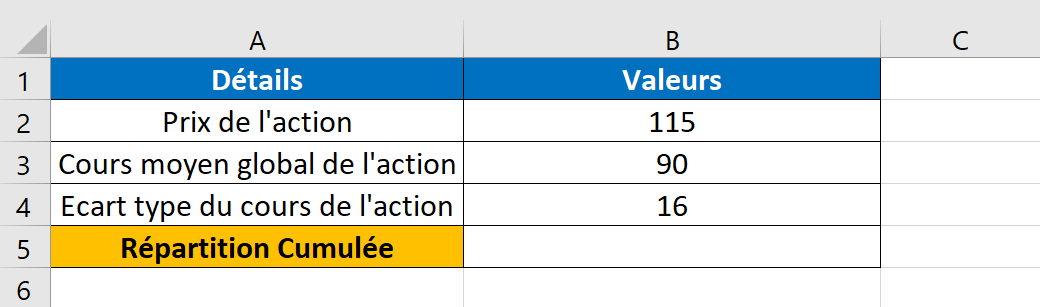
Appliquons la fonction LOI.NORMALE. N() dans Excel.

X est le cours initial de l’action. La moyenne est le prix moyen global. L’écart type est indiqué dans la cellule B4. Le type de distribution utilisé est « 1 », ce qui signifie VRAI.

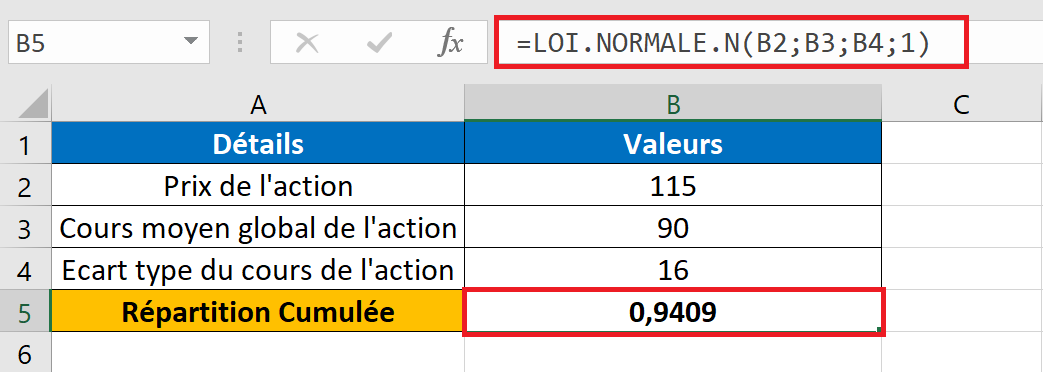
Le résultat est de 0,9409, ce qui signifie qu’environ 94 % des actions ont un prix inférieur à 115. En d’autres termes, la probabilité que l’action ait un prix supérieur à 115 est inférieure à 6 %.

Changeons le type de distribution en fonction de densité de probabilité normale, c’est-à-dire FAUX (0). Nous obtenons le résultat suivant.

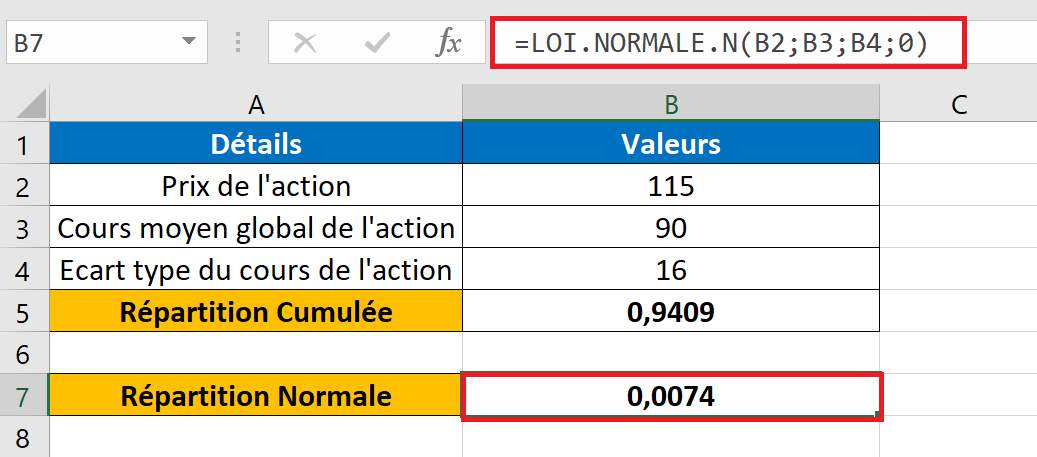
La fonction LOI.NORMALE. N renvoie la valeur 0,0074, indiquant que 0,74% des actions ont leur prix égal à 115.

Exemple n°2

Considérons les données suivantes pour une distribution normale dans Excel.

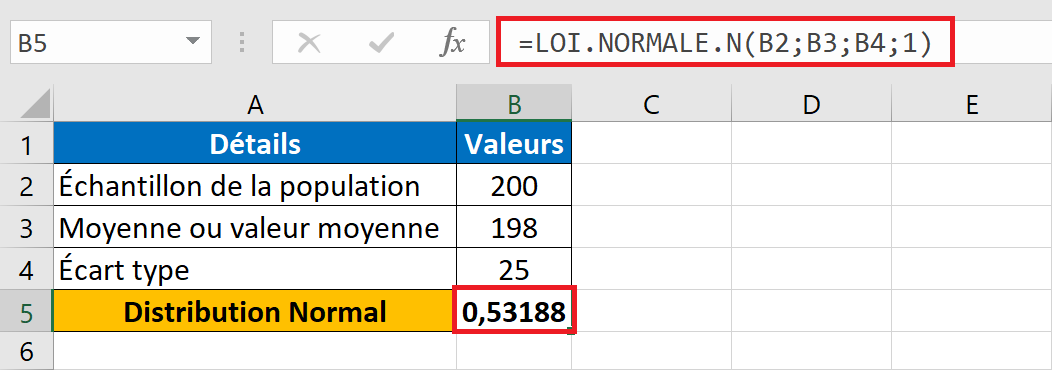
■ Échantillon de la population (X) = 200

■ Moyenne ou valeur moyenne = 198

■ Écart type = 25

Appliquons la distribution normale cumulative dans Excel.

La valeur de la distribution normale est de 0,53188, c’est-à-dire que la probabilité est de 53,18 %.

4 La fonction LOI.NORMALE.INVERSE.N()

En pratique, vous trouverez généralement que vous avez besoin de la fonction LOI.NORMALE.INVERSE.N(). C’est-à-dire que vous avez recueilli des données et que vous connaissez la moyenne et l’écart-type d’un échantillon ou d’une population. Mais où une valeur donnée tombe-t-elle dans une distribution normale ? Cette valeur peut être une moyenne d’échantillon que vous voulez comparer à la moyenne d’une population, ou il peut s’agir d’une observation individuelle que vous voulez évaluer dans le contexte d’un groupe plus large.
Dans ce cas, vous passerez l’information à LOI.NORMALE.N(), qui vous dira la probabilité relative d’observer jusqu’à une valeur particulière (Cumulative à VRAI) ou cette valeur spécifique (Cumulative à FAUX). Vous pourriez ensuite comparer cette probabilité à la probabilité d’un faux positif (le taux alpha) ou à celle d’un faux négatif (le taux bêta) que vous avez déjà adopté pour votre expérience.
La fonction LOI.NORMALE.INVERSE.N() est étroitement liée à la fonction LOI.NORMALE.N() et vous donne un angle légèrement différent sur les choses. LOI.NORMALE.N() renvoie une valeur qui représente une zone, c’est-à-dire une probabilité. LOI.NORMALE.INVERSE.N() renvoie une valeur qui représente un point sur l’axe horizontal de la courbe normale, associée à une probabilité que vous fournissez. Le point que renvoie LOI.NORMALE.INVERSE.N() est identique au point que vous fournissez en tant que premier argument de LOI.NORMALE.N().
Par exemple, la section précédente a montré que la formule = LOI.NORMALE.N (60, 54.3, 15, VRAI)
renvoie .648. La valeur 60 est égale ou supérieure à 64,8% des observations dans une distribution normale qui a une moyenne de 54,3 et un écart-type de 15. L’autre côté de la médaille: La formule
= LOI.NORMALE.INVERSE.N(0.648, 54.3, 15)
renvoie 60. Si votre distribution a une moyenne de 54,3 et un écart-type de 15, alors 64,8% de la distribution se trouve à ou au-dessous d’une valeur de 60. Cette illustration est juste, bien, illustrative. Vous n’avez normalement pas besoin de connaître le point qui atteint ou dépasse 64,8% d’une distribution.
Mais supposons qu’en préparation d’un projet de recherche, vous décidiez que vous conclurez qu’un traitement n’a d’effet fiable que si la moyenne du groupe expérimental est dans le top 5% de la population de moyens de groupes hypothétiques qui pourraient être acquis de la même manière. population normalement distribuée. (Ceci est cohérent avec l’approche traditionnelle de l’expérimentation, que les Chapitres 9 et 10 discutent beaucoup plus en détail.) Dans ce cas, vous voudriez savoir quel score sépare les 5% supérieurs des 95% inférieurs.
Si vous connaissez la moyenne et l’écart-type, LOI.NORMALE.INVERSE.N() fait le travail pour vous. Toujours en prenant la population moyenne à 54,3 et l’écart-type à 15, la formule
= LOI.NORMALE.INVERSE.N(0.95, 54.3, 15)
renvoie 78.97. Cinq pour cent d’une distribution normale qui a une moyenne de 54,3 et un écart type de 15 se situe au-dessus d’une valeur de 78,97.
Comme vous le voyez, la formule utilise 0.95 comme premier argument de LOI.NORMALE.INVERSE.N() . C’est parce que LOI.NORMALE.INVERSE.N() suppose une probabilité cumulative. Notez que contrairement à LOI.NORMALE.N(), la fonction LOI.NORMALE.INVERSE.N() n’a pas de quatrième argument Cumulative. Donc, demander quelle valeur coupe les 5% supérieurs de la distribution équivaut à demander quelle valeur coupe les 95% inférieurs de la distribution.

Dans ce contexte, choisir d’utiliser LOI.NORMALE.N() ou LOI.NORMALE.INVERSE.N() dépend en grande partie du type d’information que vous recherchez. Si vous voulez savoir quelle est la probabilité que vous observiez un nombre au moins aussi grand que X, passez X à LOI.NORMALE.N() pour obtenir une probabilité. Si vous voulez connaître le nombre qui sert de limite à une zone – une zone qui correspond à une probabilité donnée – remettez la zone à LOI.NORMALE.INVERSE.N() pour obtenir ce nombre.
Dans les deux cas, vous devez fournir la moyenne et l’écart-type. Gardez à l’esprit qu’il existe un nombre non compté de distributions normales qui ont différents moyens de définir leurs emplacements et différents écarts-types pour définir leurs écarts. Dans le cas de LOI.NORMALE.N(), vous devez également indiquer à la fonction si vous êtes intéressé par la probabilité cumulative ou l’estimation ponctuelle.

5 Utilisation de LOI.NORMALE.STANDARD.N() et LOI.NORMALE.STANDARD.INVERSE.N()

Il y a beaucoup à dire pour exprimer les distances, les poids, les durées, et ainsi de suite dans leur unité de mesure originale. C’est à cela que sert LOI.NORMALE.N(): vous fournissez ses arguments dans ces unités d’origine. Mais quand vous voulez utiliser une unité de mesure standard pour une variable distribuée normalement, vous devriez penser à LOI.NORMALE.STANDARD.N() . Il est plus rapide d’utiliser LOI.NORMALE.STANDARD.N() car vous n’avez pas à fournir la moyenne ou l’écart-type. Parce que vous faites référence à la distribution normale de l’unité, la moyenne (0) et l’écart-type (1) sont connus par définition. Tout ce que LOI.NORMALE.STANDARD.N() a besoin est le z-score et si vous voulez une zone cumulative (VRAI) ou une estimation ponctuelle (FAUX). La fonction utilise cette syntaxe simple:
= LOI.NORMALE.STANDARD.N (Z, Cumulatif)
Ainsi, le résultat de cette formule
= LOI.NORMALE.STANDARD.N(1,5 ; VRAI)
vous informe que 93,3% de la surface sous une courbe normale se trouve à gauche d’un z-score de 1,5.

Il est encore plus simple d’utiliser l’inverse de LOI.NORMALE.STANDARD.N(), qui est LOI.NORMALE.STANDARD.INVERSE.N(). Le seul argument de cette dernière fonction est une probabilité:
= LOI.NORMALE.STANDARD.INVERSE.N (0.95)
Cette formule renvoie 1,64, ce qui signifie que 95% de l’aire sous la courbe normale se trouve à gauche d’un z-score de 1,64. Si vous avez suivi un cours sur les statistiques inférentielles élémentaires, ce nombre vous semble familier, aussi familier que le 1,96 qui coupe 97,5% de la distribution.
Ce sont des nombres fréquents, car ils sont associés aux entrées «p <.05» et «p <.025» qui se produisent trop souvent au bas des tableaux dans les rapports de journal – une ornière que vous ne voulez pas obtenir coincé dans. Chapitres 9 et 10 ont beaucoup plus à dire sur ces sortes d’entrées, dans le contexte de la distribution t (qui est étroitement liée à la distribution normale).

6 Les usages

Cette fonction mathématique est appliquée dans divers domaines d’études, qu’il s’agisse des sciences, économie, statistiques, finance, affaires, investissement, psychologie, santé, génétique, biotechnologie ou universitaires. Certaines de ses applications typiques sont décrites ci-dessous :

■ Le graphique technique du marché boursier est souvent une courbe en cloche, permettant aux analystes et aux investisseurs de faire des déductions statistiques sur le rendement et le risque attendus des actions.

■ Il est utilisé pour déterminer le meilleur moment pour les entreprises de pizza de livrer des pizzas et des applications similaires dans la vie réelle.

■ Il est également appliqué dans les Operations commerciale pour déterminer l’efficacité des produits, des ressources et des ventes.

■ Il est utilisé pour comparer les tailles d’une population donnée dans laquelle la plupart des personnes auront des tailles moyennes. Très peu de personnes auront une taille supérieure ou inférieure à la moyenne.

■ Ils sont utilisés pour déterminer le rendement scolaire moyen des étudiants. Cette fonction mathématique est utilisée pour déterminer le rang d’un élève.

La fonction gaussienne est couramment utilisée en science des données et en analyse de données. Les technologies avancées telles que l’intelligence artificielle (IA) et l’apprentissage automatique peuvent fournir de meilleurs résultats lorsqu’elles sont utilisées avec des fonctions de densité normales.

La fonction LOI.NORMALE.N calcule le PDF (fonction de densité de probabilité ) et le CDF (fonction de distribution cumulative ) d’un ensemble de données. La fonction renvoie la probabilité que la variable X tombe en dessous ou à une valeur donnée. Le CDF renvoie la probabilité d’un nombre inférieur à une valeur donnée. Le PDF renvoie la probabilité d’un nombre en un point de l’ensemble de données. Si la valeur cumulée est « vrai », la fonction LOI.NORMALE.N renvoie une valeur égale à la zone située sur le côté gauche de l’entrée. Cependant, si la valeur cumulée est « fausse », la fonction renvoie une valeur qui correspond à la valeur d’entrée sur la courbe.