■■ Comment puis-je estimer la probabilité qu’une machine fonctionne sans défaillance pendant au moins 20 heures?

■■ Comment puis-je estimer la probabilité que la pose de cloisons sèches dans un bâtiment prenne plus de 200 heures?

La variable aléatoire de Weibull est une variable aléatoire continue qui est souvent utilisée pour modéliser la durée de vie d’une machine. Si vous disposez de données sur la durée de fonctionnement de machines similaires dans le passé, vous pouvez estimer les deux paramètres (alpha et bêta) qui définissent une variable aléatoire Weibull. Vous pouvez ensuite utiliser la fonction WEIBULL.DIST dans Microsoft Excel  pour déterminer les probabilités d’intérêt telles qu’une estimation de la durée de fonctionnement d’une machine sans échec.

La variable aléatoire bêta est une variable aléatoire continue qui est souvent utilisée pour modéliser la durée d’une activité. Étant donné les estimations de la durée minimale, de la durée maximale, de la durée moyenne et de l’écart-type de la durée, vous pouvez utiliser la fonction BETA.DIST dans Excel 2013 pour déterminer les probabilités d’intérêt.

Réponses aux questions de ce chapitre

Cette section fournit les réponses aux questions répertoriées au début de cet article .

Comment puis-je estimer la probabilité qu’une machine fonctionne sans échouer pendant au moins 20 heures?

Supposons que vous ayez observé la durée de vie de sept machines similaires. Les données collectées sur les machines est contenue dans le fichier , illustré à la figure 1.

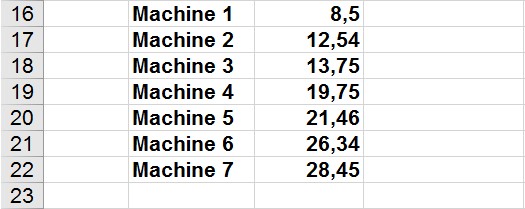
FIGURE 1 Données de durée de vie de la machine.

Les ingénieurs de fiabilité ont constaté que la variable aléatoire Weibull est généralement appropriée pour modéliser la durée de vie des machines. La variable aléatoire Weibull est spécifiée par deux paramètres: alpha et bêta. Sur la base des données, vous pouvez déterminer (en utilisant les fonctions MOYENNE et STDEV.S dans les cellules B13 et B14) que, en moyenne, une machine dure 18,68 heures, avec un écart type de 7,40 heures. En copiant ces valeurs dans les cellules G6 et G11 et en exécutant le solveur avec les paramètres indiqués dans la figure 2, vous pouvez trouver des estimations de l’alpha et du bêta qui garantissent que la variable aléatoire de Weibull aura un écart moyen et standard correspondant aux données. Dans ce cas, alpha est égal à 2,725 et bêta est égal à 21.003, comme vous pouvez le voir sur la figure 3. Toute valeur que vous entrez pour alpha et bêta dans les cellules E2 et E3 pour une variable aléatoire Weibull donne une moyenne (calculée dans la cellule E6) et un écart-type (calculé dans la cellule E11). Le modèle Solver fait varier alpha et bêta jusqu’à ce que la moyenne et l’écart-type de la distribution de Weibull soient égaux à la moyenne et à l’écart-type de la durée de vie de la machine calculés à partir de vos données.

L’option Multistart pour le moteur non linéaire GRG est recommandée pour cela. Le moteur à plusieurs départs fonctionne mieux avec les limites supérieure et inférieure des cellules changeantes. Une limite inférieure de 0,010 sur alpha et la bêta fonctionnera toujours. Une limite supérieure de 1 000 pour alpha et bêta a été essayée. Si le solveur fait bousculer l’alpha ou la bêta contre votre limite supérieure, vous devez relâcher la limite.

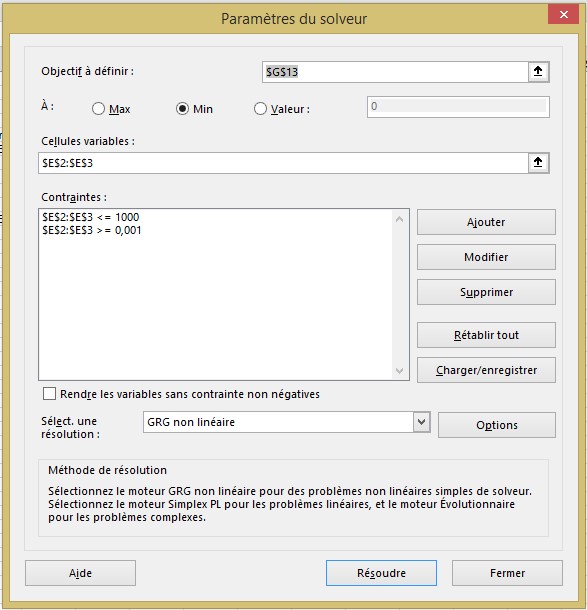
FIGURE 2 Paramètres du solveur pour déterminer les paramètres d’une variable aléatoire de Weibull.

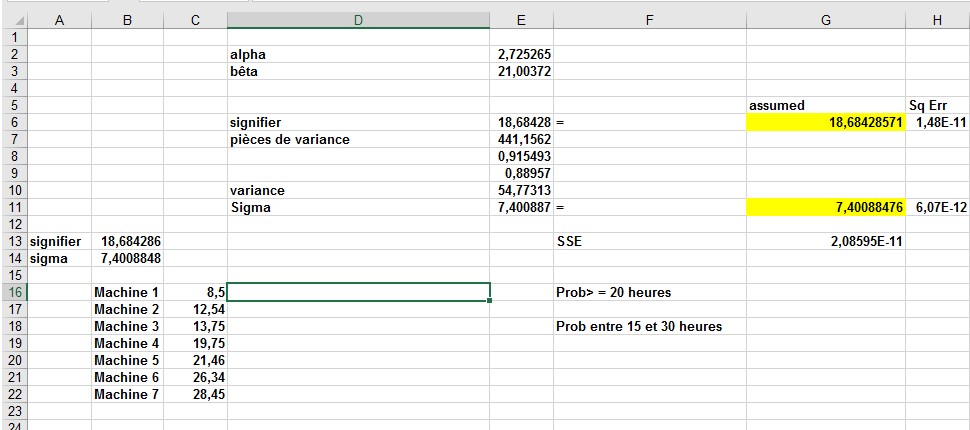
FIGURE 3 Estimations de l’alpha et du bêta pour une variable aléatoire de Weibull.

Voici la syntaxe de la fonction LOI.WEIBULL.N:

LOI.WEIBULL.N (x, alpha, beta, cumulatif)

Lorsque Cumulative est égal à Vrai, cette formule entraîne la probabilité qu’une variable aléatoire de Weibull avec les paramètres alpha et beta soit inférieure ou égale à x. Changer True à False donne la hauteur de la fonction de densité de probabilité de Weibull (pdf). Rappelez-vous du chapitre 66, «Une introduction aux variables aléatoires», que la hauteur d’un pdf pour n’importe quelle valeur x d’une variable aléatoire continue.

indique la probabilité que la variable aléatoire prenne une valeur proche de x. Ainsi, si la densité de Weibull pendant 20 heures était le double de la densité de Weibull pendant 10 heures, vous sauriez qu’une machine est deux fois plus susceptible de travailler pendant 20 heures avant d’échouer que de travailler pendant 10 heures avant d’échouer. Avant de répondre à certaines questions impliquant des probabilités d’intérêt, notez que dans les versions antérieures d’Excel, la fonction WEIBULLDIST donne les mêmes résultats que LOI.WEIBULL.N:

■■ Quelle est la probabilité qu’une machine dure au moins 20 heures? Cette probabilité (41,7%) est calculée dans la cellule G16 avec la formule 1-WEIBULL.DIST (20, alpha, beta, 1). Essentiellement, cette formule calcule la zone sous le pdf de Weibull à droite de 20 heures en soustrayant de 1 la zone à gauche de 20 heures.

■■ Quelle est la probabilité qu’une machine dure de 15 à 30 heures? Cette probabilité (66,9%) est calculée dans la cellule G18 avec la formule LOI.WEIBULL.N (30, alpha, beta, TRUE) – WEIBULL.DIST (15, alpha, beta, TRUE). Cette formule trouve la zone sous le pdf Weibull de 15 à 30 heures en calculant la zone à gauche de 30 heures moins la zone à gauche de 15 heures. Après avoir soustrait la probabilité qu’une machine fonctionne sans défaillance pendant moins de 15 heures de la probabilité d’une machine   soit sans défaillance pendant moins de ou égale à 30 heures, il vous reste la probabilité qu’une machine fonctionne sans défaillance de 15 à 30 heures.

Comment puis-je estimer la probabilité que la suspension de cloisons sèches dans un bâtiment prenne plus de 200 heures?

Depuis le développement du missile Polaris dans les années 1950, les chefs de projet ont modélisé les durées d’activité avec la variable aléatoire bêta. Pour spécifier une variable aléatoire bêta, vous devez spécifier une valeur minimale, une valeur maximale et deux paramètres (alpha et bêta). Les données du fichier (voir la figure 4) peuvent être utilisées pour estimer les paramètres d’une distribution bêta.

Supposons que vous pensiez que le temps nécessaire pour suspendre les cloisons sèches dans un bâtiment est 0 et 600 heures. Ce sont vos valeurs minimales et maximales, saisies dans les cellules C7 et C8. La gamme de cellules F8: F22 contient le temps nécessaire pour suspendre les cloisons sèches dans 15 bâtiments de taille similaire. Dans la cellule F5, la fonction MOYENNE a été utilisée pour calculer le temps moyen (78,49 heures) nécessaire pour accrocher des cloisons sèches dans ces 15 bâtiments. Dans la cellule F6, la fonction ECARTYPE a été utilisée pour déterminer l’écart type (47,97 heures) du temps nécessaire pour suspendre les cloisons sèches dans ces bâtiments. Tout choix de valeurs alpha et bêta détermine la forme du pdf de la distribution bêta et la moyenne et l’écart-type de la variable aléatoire bêta correspondante. Si vous pouvez choisir des valeurs alpha et bêta pour correspondre à la moyenne et l’écart type des temps d’installation des cloisons sèches calculés à partir de ces données, il semble raisonnable que ces valeurs alpha et bêta produiront des probabilités cohérentes avec les données observées. Après avoir entré la moyenne et l’écart type des données d’installation de cloison sèche dans les cellules C9 et C10, la feuille de calcul calcule les valeurs d’alpha (2,20) dans la cellule C5 et de bêta (14,66) dans la cellule C6 qui garantissent que la moyenne et l’écart type de la variable aléatoire bêta correspondent à la moyenne et à l’écart type des données.

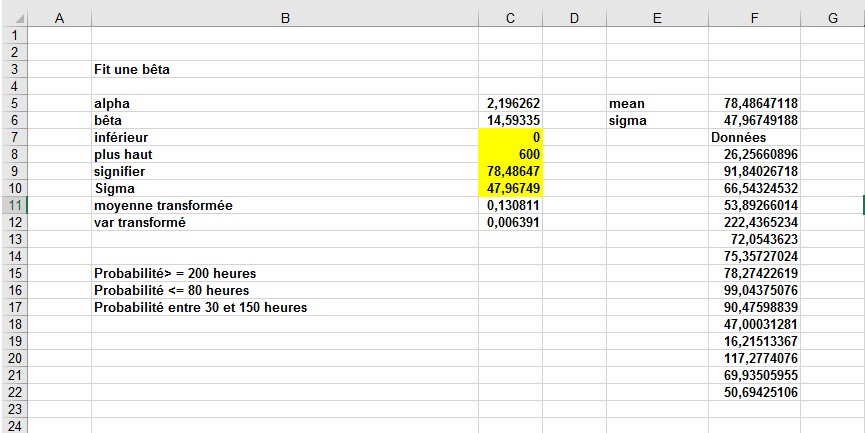
FIGURE 4 Détermination des probabilités avec la variable aléatoire bêta.

La fonction LOI.BETA.N (x, alpha, bêta, Vrai_ou_1, inférieur, supérieur) détermine la probabilité qu’une variable aléatoire bêta allant de inférieur à supérieur, avec les paramètres alpha et bêta, assume une valeur inférieure ou égale à x. Les deux derniers paramètres sont facultatifs, et s’ils sont omis, Excel suppose que inférieur est égal à 0 et supérieur égal à 1. La fonction LOI.BETA.N (x, alpha, bêta, Faux_ou_0, inférieur, supérieur) renvoie le pdf pour une variable aléatoire suivant un distribution bêta. Vous pouvez maintenant utiliser la fonction LOI.BETA.N pour déterminer les probabilités d’intérêt.

Pour calculer la probabilité que la cloison sèche suspendue prenne au moins 200 heures, vous pouvez utiliser la formule dans la cellule C15, 1 – LOI.BETA.N (200, alpha, beta, True_or_1, inférieur, supérieur). Le résultat est de 2,1%. Cette formule calcule simplement la probabilité que la cloison sèche suspendue prenne au moins 200 heures, car 1 – la cloison sèche probable est inférieure ou égale à 200 heures.

La probabilité que la cloison sèche suspendue prenne au plus 80 heures (58,3%) peut être calculée avec la formule dans la cellule C16, LOI.BETA.N (80, alpha, beta, Vrai, inférieure, supérieure). Et pour calculer la probabilité que la tâche dure entre 30 et 150 heures (77,1%), dans la cellule C17, utilisez le LOI.BETA.N (150, alpha, beta, Vrai, inférieur, supérieur) – LOI.BETA.N ( 30, alpha, beta, Vrai, inférieur, supérieur) formule. Cette formule calcule la probabilité que les cloisons sèches prennent de 30 à 150 heures, comme la probabilité que les cloisons sèches prennent moins ou égal à 150 heures moins la probabilité que les cloisons sèches prennent moins ou égal à 30 heures. La différence entre ces probabilités ne compte que les cas où les cloisons sèches prennent de 30 à 150 heures.