Syntaxe. ACOS(nombre)
Définition. L’arc cosinus est l’angle dont le cosinus est le nombre.
Arguments
nombre(obligatoire) Le cosinus de l’angle, doit être compris entre -1 et 1
Arrière-plan.
Utilisez la fonction ACOS() pour calculer l’angle adjacent en fonction du cosinus (voir Figure). Le résultat est une mesure en radians et doit être converti en degrés avec la fonction DEGRES(). Étant donné que chaque angle se produit deux fois dans un cercle complet, la plage de valeurs d’un arccosinus est restreinte :
Si l’angle est calculé en radians, la plage de valeurs s’étend de 0 à n (pi).
Si l’angle est calculé en degrés, la plage de valeurs s’étend de 0 à 180 degrés.
L’arccosinus est strictement monotone décroissant. Les valeurs de l’arc cosinus dans un plan de coordonnées créent le graphique illustré à la Figure.
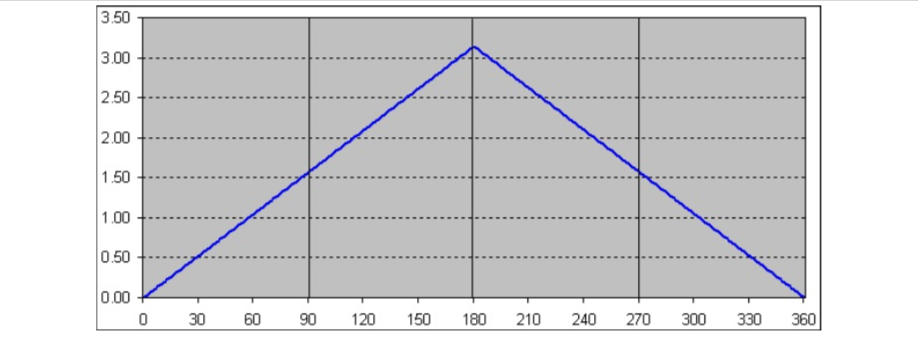
Illustration. La fonction ACOS().
Exemples.
Les exemples suivants illustrent la fonction ACOS().
Exemple 1.Une échelle de 30 pieds s’appuie contre une maison. La distance entre le bas de l’échelle et le mur est de 7 pieds. Quel est l’angle d’inclinaison ?
Tout d’abord, vous calculez le cosinus de la jambe adjacente (la distance au mur) et l’hypoténuse (longueur de l’échelle).
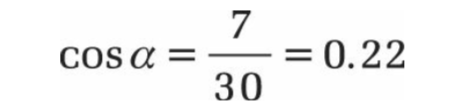
L’angle est calculé à partir du cosinus :
=DEGRES(ACOS(7/30))
L’angle d’inclinaison est de 76,51° ou 76° et 51 minutes. Étant donné que la fonction ACOS() renvoie une mesure en radians, vous devez convertir le résultat en degrés.
Exemple 2. L’angle résultant du cosinus 0,707106781 pourrait être aussi bien de 45° que de 315°. La plage étant limitée de 0° à 180°, le résultat est de 45°. La formule correspondante ressemble à ceci :
=DEGRES(ACOS(0,707106781))
Le résultat étant une mesure en radians, vous devez le convertir à l’aide de la fonction DEGRES(). Voici quelques exemples supplémentaires:
=acos (0) renvoie la mesure en radian 570796327et un angle de 90°.
=acos (-0,5) renvoie la mesure en radian 094395102 et un angle de 120°.
=acos (-1) renvoie la mesure en radian 141592654et un angle de 180°.
