Syntaxe. BESSELJ(x;n)

Définition.

Cette fonction renvoie la fonction de Bessel de première espèce, Jn(x).

Arguments

x (requis) La valeur pour laquelle la fonction doit être évaluée ; x doit être un nombre réel et peut avoir des valeurs comprises entre -1,34·10^8 et +1,34·40^8. (La plage de valeurs varie en fonction de l’ordre n.)
n(obligatoire) L’ordre de la fonction de Bessel ; doit être positif. Si ni n’est pas un entier, les décimales sont ignorées et non arrondies.
Arrière-plan.

La fonction de Bessel de première espèce Jn(x) est la solution de la différentielle de Bessel

équation

x2y”+ xy’+ (x2- n2)• y = 0

ou

Pour un nombre réel v, la fonction peut être calculée avec

où r(y) est la fonction gamma.

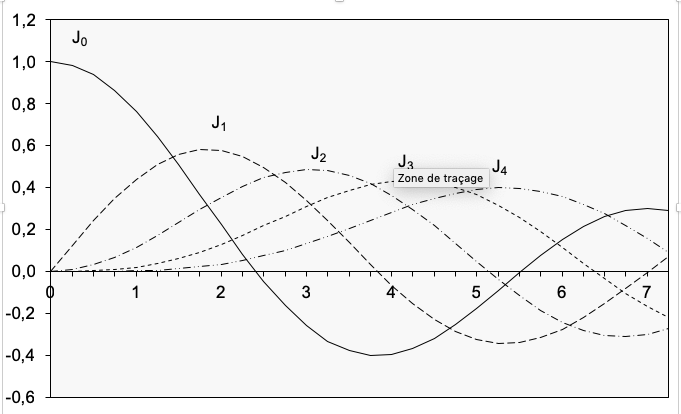
Exemple. En raison du caractère très particulier des fonctions de Bessel, ce livre n’utilise que leur représentation graphique, comme pour les autres fonctions de Bessel.

Dans la feuille de calcul illustrée à la Figure, que vous pouvez également trouver dans les exemples de fichiers, les valeurs de la fonction pour BESSELJ() sont calculées avec les ordres 0 à 4 et affichées dans un graphique.

Image. Calcul de la fonction BESSELJ() pour les ordres n = 0…4 (extrait).