Syntaxe. BESSELK(x;n)

Définition.

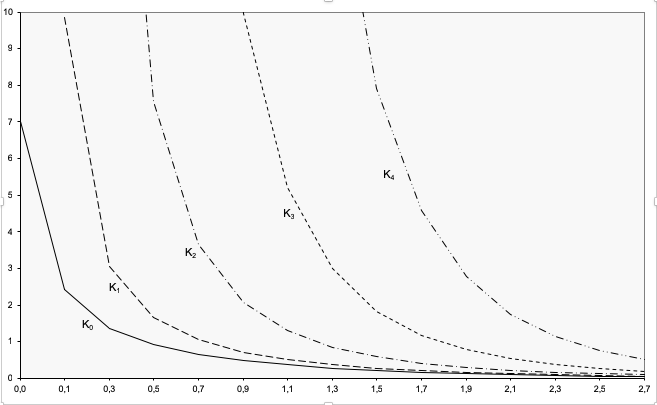
Cette fonction renvoie la fonction de Bessel modifiée de seconde espèce, Kn(x).

Arguments

x(requis) La valeur pour laquelle la fonction doit être évaluée ; x doit être un nombre réel et peut avoir des valeurs de +1·10^-307 à plus de +700. La valeur exacte de la limite supérieure de x dépend de l’ordre n (et l’inverse est également vrai), mais elle est supérieure à tous les nombres utilisés en pratique.
n(obligatoire) L’ordre de la fonction de Bessel ; doit être positif et un entier supérieur à 100. En pratique, cependant, il n’y a que des ordres inférieurs à 10. Si ni n’est pas un entier, les décimales sont ignorés. c’est-à-dire qu’il est tronqué et non arrondi.

Arrière-plan.

Kn(x)correspond aux fonctions de Bessel Jn et Ynevaluées pour des arguments purement imaginaires. Parfois, on l’appelle la fonction de Basset, la fonction de Macdonald ou la fonction de Bessel modifiée du troisième type. C’est la solution de l’équation différentielle de Bessel modifiée.

x2y » + xy’- (x2+ n2)· y= 0

ou

La fonction de Bessel modifiée de deuxième espèce, Kn(x) d’ordre n, peut être exprimée en fonction de la fonction de Bessel modifiée de première espèce, In(x) :

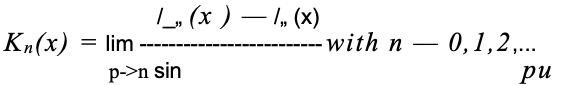
Exemples.

En raison du caractère très particulier des fonctions de Bessel, ce chapitre n’utilise que leur représentation graphique, comme pour les autres fonctions de Bessel.

Dans la feuille de travail illustrée à la Figure, les valeurs de fonction de la fonction BESSELK() pour les ordres n= 0…4 peuvent être calculées et affichées graphiquement, comme illustré à la Figure.

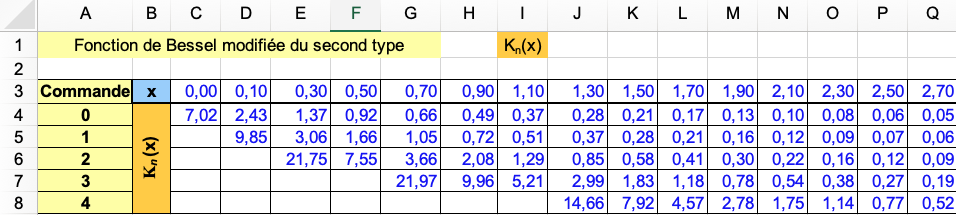
Pour les ordres supérieurs, les premières formules sont omises, car leurs valeurs de fonction sont trop grandes pour un graphique clair.