BETA.INVERSE (probabilité; alpha; bêta; [A]; [B])

Définition.

Cette fonction renvoie l’inverse d’une distribution bêta. Si probabilité = LOI.BETA.N (x; …), alors BETA.INVERSE (probabilité; …)=x. BETA.INVERSE() est la fonction inverse de LOI.BETA.N().

La distribution bêta peut être utilisée dans la planification de projet pour modéliser les délais de réalisation en fonction du délai de réalisation et de la variance prévus. L’inverse de la fonction renvoie la valeur x (temps de réalisation) pour une probabilité donnée de la distribution de fréquence cumulative bêta.

Arguments

-probabilité(obligatoire). Une probabilité associée à la distribution beta

-alpha(obligatoire). Un paramètre de la distribution (décrit la forme)

-beta (obligatoire). Un paramètre de la distribution (décrit la forme)

-A (facultatif). La limite inférieure de l’intervalle pour x

-B (facultatif). La limite supérieure de l’intervalle pour x

Les arguments alpha et beta décrivent la forme de la distribution beta. Les limites inférieure et supérieure transcrivent les valeurs de 0 et 1. Si A est fourni, alors B doit également être fourni.

REMARQUE
Si l’un des arguments n’est pas une valeur numérique, la fonction BETA.INVERSE() renvoie le #VALUE! Erreur.
Si alpha ou bêta est inférieur ou égal à 0, la fonction BETA.INVERSE() renvoie le #NUM! Erreur.
Si la probabilité est inférieure ou égale à 0 ou supérieure à 1, la fonction BETA.INVERSE() renvoie le #NUM! Erreur.

Si vous n’entrez pas de valeurs pour A et B, la fonction BETA.INVERSE() utilise la distribution standard, A=0 et B=1.
Si probabilité a une valeur, BETA.INVERSE() recherche la valeur x pour que LOI.BETA(x, alpha, bêta, A, B) = probabilité. Par conséquent, la précision de BETA.INVERSE() dépend de celle de LOI.BETAT(). BETA.INVERSE() utilise une technique de recherche itérative. Si la recherche n’a pas convergé après 100 itérations, la fonction renvoie l’erreur #N/A.

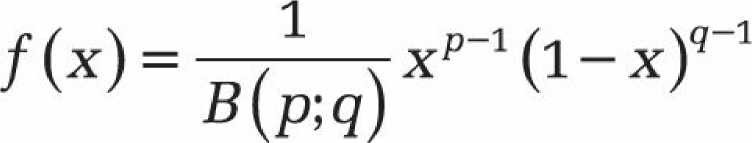
Contexte.

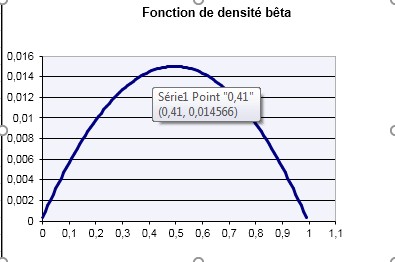
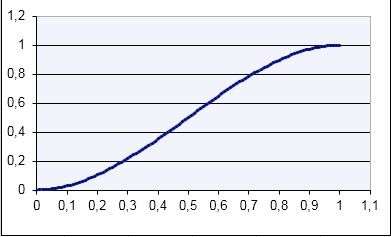
La distribution bêta est une distribution de probabilité continue indiquant la probabilité qu’une variable aléatoire x ait une certaine valeur dans l’intervalle [0,1].

La distribution bêta est définie par la densité de probabilité

En dehors de l’intervalle [0,1], il est poursuivi avec f(x)=0. Les paramètres sont p et q. Pour assurer la normalisation, p, q doit être supérieur à 0. Le préfacteur 1/B (p;q) assure la normalisation correcte (la normalisation à une valeur comprise entre 0 et 1). L’expression

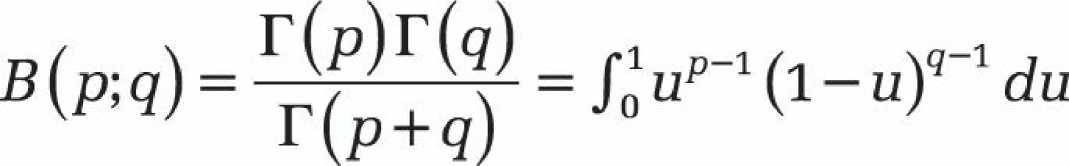
représente la fonction bêta. r (p) est la fonction gamma.

La fonction bêta (ou fonction bêta d’Euler) est une fonction mathématique de deux nombres réels positifs ou de deux nombres complexes x et y, définis par la formule suivante:

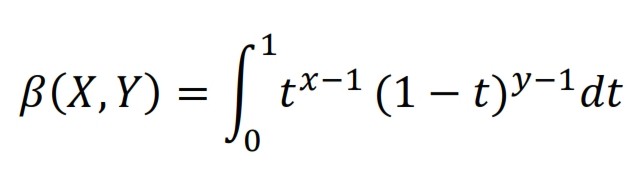
La formule est souvent notée B (x, y). Excel utilise la distribution cumulative.

Les équations suivantes démontrent la valeur et la variance attendues de la distribution bêta cumulative:

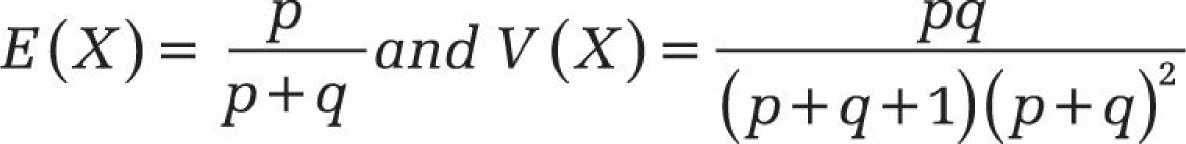
La fonction BETA.INVERSE() renvoie l’inverse de la distribution bêta.

Exemple.

Pour vous entraîner à calculer BETA.INVERSE(), utilisez les exemples de valeurs suivants:

0,685470581 = la probabilité associée à la distribution bêta

8 = paramètre de la distribution

10 = paramètre de la distribution

1 = limite inférieure ■ 3 = limite supérieure

Avec ces paramètres, la fonction BETA.INVERSE() renvoie le quantile 2 pour la distribution bêta donnée.

Vous avez décrit la forme de la distribution bêta cumulative avec les paramètres de distribution 8 et 10. Vous voulez savoir quelle valeur vous pourriez espérer avec une probabilité de 0,6854. Le résultat serait renvoyé dans une plage allant de 0 à 1, mais étant donné que vous utilisez respectivement les limites inférieure et supérieure de 1 et 3, la réponse est convertie en cette plage, ce qui donne 2.