Syntaxe

CENTILE (Matrice; k)

Définition.

Cette fonction renvoie le quantile alpha d’un ensemble de données. Vous pouvez utiliser cette fonction pour établir un seuil d’acceptation. Par exemple, vous pouvez décider d’inviter uniquement les clients dont les ventes dépassent le 80e centile à une fête. En statistique, le quantile de p pour cent pour une fonction de probabilité est la valeur de la plage d’événements avec la valeur p pour cent de la fonction de densité. p pour cent des observations ou la population est inférieure au quantile p pour cent.

Arguments

-tableau (obligatoire). Tableau ou plage de données définissant le statut relatif de l’alpha de données (obligatoire).

-Une valeur comprise entre 0 et 1 inclus

REMARQUE
Si le tableau est vide ou contient plus de 8 191 points de données, CENTILE () renvoie le #NUM! Erreur. Si alpha n’est pas une expression numérique, la fonction CENTILE () renvoie le #VALUE! Erreur. Si alpha est inférieur à 0 ou supérieur à 1, la fonction CENTILE () renvoie le #NUM! Erreur. Si alpha n’est pas un multiple de 1 / (n – 1), CENTILE() interpole pour déterminer la valeur du quantile alpha.

Contexte.

Un quantile est une partie définie d’un ensemble de données trié par taille. Les quantiles (sauf la médiane) sont des valeurs qui définissent la variance d’un ensemble de données. Certains des quantiles les plus importants sont le décile, le quartile et la médiane. La médiane correspond au quantile à 50%. En d’autres termes, le p quantile d’une distribution indique quelle valeur sépare le p * 100% inférieur des valeurs de données du 100 – p * 100 supérieur supérieur. Si vous spécifiez le quantile 0,65 d’une distribution, 65% des données sont inférieures ou égales à la valeur de données et 35% des données sont supérieures ou égales à cette valeur.

Parfois, aucune valeur dans l’ensemble de données ne correspond à la valeur correspondante. Une règle pour les calculs de quantiles est (n = nombre de valeurs de données): Si n * p n’est pas un entier, l’entier suivant est utilisé comme nombre ordinal pour la valeur de quantile. Si n * p est un entier, le quantile est une valeur comprise entre n * p et n * p + 1. Lorsqu’il existe 16 valeurs de données, le quantile 0,25 (le premier quartile) porte le nombre ordinal 4 (16 * 0,25).

Le quantile 0,25 ou le premier quartile doit être situé entre les 25% inférieurs et 75% supérieurs. Par conséquent, il est judicieux de définir une valeur entre la quatrième et la cinquième valeur de l’ensemble de données trié. Le premier décile peut être défini par le nombre ordinal pour n * p = 1,6. Dans cet exemple, il s’agit de la deuxième valeur de l’ensemble de données. Au moins 10% des données sont inférieures ou égales à cette valeur et 90% des données sont supérieures ou égales à cette valeur.

Exemple.

Reprenons l’exemple de la société de logiciels. Vous êtes le responsable du service de contrôle et générez les numéros de vente des différentes unités de gestion pour une année complète. Vous souhaitez maintenant séparer les données pour les analyser plus en profondeur. L’objectif est de générer des valeurs de vente dépassant le quantile 0,6 (60ème centile).

Avec Excel, vous pouvez calculer n’importe quel p-quantile. Pour l’argument alpha, vous devez entrer le pourcentage sous forme de nombre décimal. Vous calculez les résultats par incréments de 10%. Comme vous pouvez le voir sur la figure, les résultats sont triés par ordre croissant. Vous pouvez maintenant analyser toutes les ventes supérieures ou égales au quantile 0,6.

 Les quantiles sont calculés par incréments de 10%.

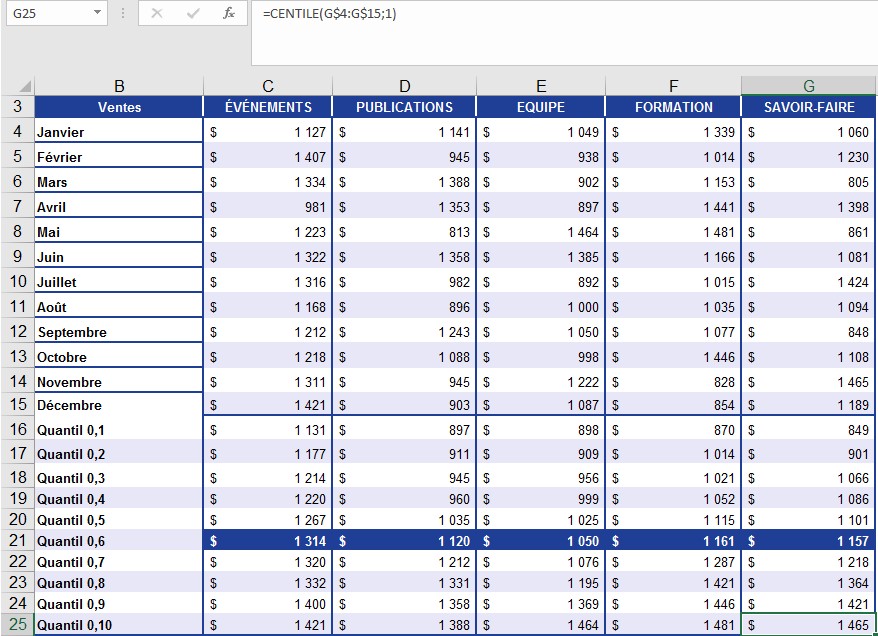
Le quantile 0,6 indique que 60% des valeurs des données d’origine sont inférieures à la valeur et 40% supérieures ou égales à cette valeur.