Syntaxe.
CHISQ.TEST(plage_réelle; plage_attendue)
Définition.
Cette fonction renvoie la statistique de test d’un X2-test d’indépendance. CHISQ.TEST() renvoie la valeur de la distribution chi-carré (X2) pour la statistique et les degrés de liberté appropriés. Vous pouvez utiliser les tests C2 pour déterminer si les résultats supposés sont vérifiés.
Arguments
■ plage_réelle (requis). La plage de données contenant des observations à tester par rapport aux valeurs attendues
■ plage attendue (obligatoire). La gamme d’observations attendues

REMARQUE
Si la plage actuelle et la plage attendue ont un nombre différent de points de données, la fonction CHISQ.TEST() renvoie l’erreur #N/A. 22
Le test c calcule d’abord une statistique c en utilisant la formule suivante:
Contexte.
Le test du chi carré fournit une méthode pour tester l’association de variables dans un tableaude chemin. L’hypothèse nulle suppose qu’il n’y a pas d’association, tandis que l’hypothèse alternative suppose qu’il existe une certaine association, bien que cette hypothèse alternative ne soit pas plus spécifique que celle-ci. Le test du chi carré mesure l’écart entre les valeurs observées dans le tableau à deux voies et celles attendues avec l’hypothèse nulle (pas d’association). Le tableau à double entrée des valeurs attendues peut être calculé à partir des totaux des lignes et des colonnes.
La fonction CHISQ.TEST() renvoie le test d’indépendance en comparant les valeurs existantes aux valeurs attendues.
Le niveau de signification, avec une valeur numérique comprise entre 0 et 100%, indique le niveau de confiance dans le test d’hypothèse. Une signification de 90% ne signifie pas que:
■ La probabilité que les données existantes soient aléatoires n’est que de 10%.
■ Un certain fait a une probabilité de 90% d’être vrai.
Le niveau de signification indique le pourcentage d’erreurs autorisées pour qu’un échantillon soit toujours considéré comme aléatoire.
Exemple.
Vous êtes un fabricant de vitamines et vous souhaitez vérifier si l’utilisation régulière de vitamine C réduit le risque de rhume. Vous avez prélevé deux échantillons dans la même population, où 22 des 936 participants ont eu un rhume. Le premier échantillon contient les valeurs attendues et le deuxième échantillon contient les valeurs observées.
Dans la première étape, vous voulez déterminer le niveau de signification des valeurs pour vérifier si les échantillons sont aléatoires et si les valeurs sont similaires. Vous utilisez la fonction CHISQ.TEST(), comme illustré à la figure .
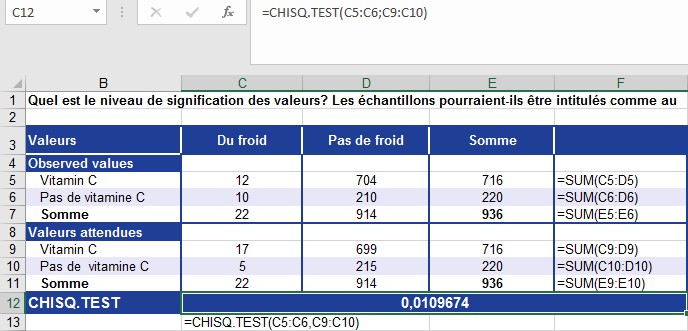
Figure . Calcul de CHISQ.TEST() avec les valeurs observées et attendues.
Le seuil de signification calculé de 1% indique que les chiffres d’incidence observés et existants dans 99% (100 moins 1) des cas présentent des caractéristiques comparables. Cela suggère que les échantillons sont aléatoires. c’est-à-dire que l’échantillon prélevé ne diffère pas de manière significative de ce à quoi on pourrait s’attendre avec le niveau de rhume et l’incidence de l’utilisation de vitamine C dans la population.
La valeur calculée par CHISQ.TEST() peut également indiquer la probabilité d’un v calculé. La variable v est un indicateur statistique qui caractérise une mesure de l’écart total.
Pour calculer la variable, utilisez la formule suivante:
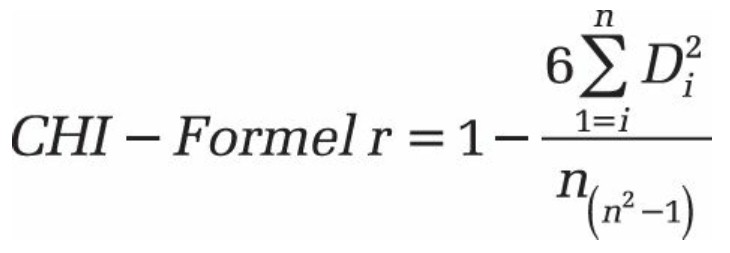
Si la valeur de la statistique n est très élevée, l’hypothèse nulle est rejetée. Si la probabilité pour v est inférieure au niveau de signification correspondant, la différence est significative. Cela signifie que l’hypothèse alternative est supposée. Si la probabilité pour v est plus grande, la différence n’est pas significative et l’hypothèse nulle est supposée.
