Syntaxe. DETERMAT(matrice)

Définition.

Cette fonction renvoie le déterminant d’un tableau.

Argument

matrice(obligatoire) Un tableau numérique avec un nombre égal de lignes et de colonnes
Arrière-plan.

Le calcul du déterminant est basé sur un tableau numérique. Un tableau peut être donné comme suit :

Une plage de cellules (par exemple, A1:C3)
Une constante matricielle (par exemple, {1,2,3;4,5,6;7,8,9})
Nom d’une plage de cellules ou d’une constante matricielle
Si les cellules du tableau sont vides ou contiennent du texte, la fonction DETERMAT() renvoie la #valeur ! Erreur. Si le tableau n’a pas un nombre égal de lignes et de colonnes, la fonction DETERMAT() renvoie la #value ! Erreur.

Les déterminants sont généralement utilisés pour résoudre des systèmes d’équations. Si le déterminant est nul, l’équation n’a pas de solution (définie).

Pour calculer le déterminant du tableau A, utilisez les formules suivantes :

Si A est une matrice 1×1 : det(A) = a11
Si A est une matrice 2×2 :
det(A)= a11 • a22 – a12 • a21

Si A est une matrice 3×3 :
det(A)= a11 • a22 • a33 + a12 • a23 • a31 + a13 • a21 • a32 – a13 • a22 • a31 – a12 • a21 • a33 – a11 • a23 • a32

Gottfried Leibniz (philosophe et mathématicien allemand, 1646-1716) a développé les formules de Leibniz comme une formule commune pour un n • n DETERMAT :

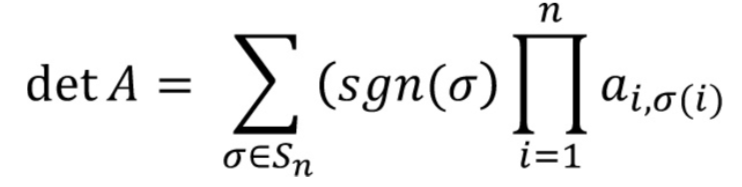
Exemple. Voir l’exemple de la fonction INVERSEMAT().