Syntaxe.
DROITEREG (y_connus; [x_connus]; [constante]; [statistiques])
Définition.
Cette fonction calcule les statistiques d’une ligne en utilisant les plus petits carrés pour calculer une ligne droite appropriée aux données, puis renvoie un tableau décrivant une ligne. Comme cette fonction retourne un tableau de valeurs, il doit être entré sous forme de formule matricielle.
L’équation de la ligne est la suivante:
y = mx + b
ou, s’il existe plusieurs plages de valeurs x: y = m1x1 + m2x2 + … + b
Les valeurs y dépendantes sont fonction des valeurs x indépendantes. Les valeurs m sont des coefficients correspondant à chaque valeur x et b est une valeur constante. Notez que y, x et m peuvent être des vecteurs. Le tableau renvoyé par la fonction DROITEREG () est {mn, mn-i, …, mi, b}. LINEST () peut également renvoyer des statistiques de régression supplémentaires (voir le tableau 12-2 plus loin dans cette section).
Arguments
■ y_connus (requis). Les valeurs y que vous connaissez déjà de la relation y = mx + b
– Si le tableau y_connus consiste en une seule colonne, chaque colonne du tableau x_connus est interprétée comme une variable distincte.
– Si le tableau y_connus consiste en une seule ligne, chaque ligne du tableau de x connu est interprétée comme une variable distincte.
■ x_connus (facultatif). Les valeurs x que vous connaissez déjà de la relation y = mx + b
– Le tableau x connu peut inclure un ou plusieurs ensembles de variables. Si une seule variable est utilisée, non_y et x_connus peuvent être des plages de n’importe quelle forme, à condition que leurs dimensions soient égales. Si plusieurs variables sont utilisées, y_connus doit être un vecteur (une plage composée d’une seule ligne ou d’une seule colonne).
– Si x_connus n’est pas spécifié, il est supposé être le tableau {1,2,3, …} contenant le même nombre d’éléments que le paramètre y_connus.
■ const (facultatif). Une valeur logique spécifiant s’il faut forcer la constante b à être égale à 0
– Si conSt est VRAI ou omis, b est calculé normalement.
– Si conSt est FAUX, alors b est égal à 0 et les valeurs m sont ajustées à y = m.
■ stats (facultatif). Une valeur logique spécifiant s’il faut renvoyer des statistiques de régression supplémentaires
– Si Stats est VRAI, la fonction DROITEREG () renvoie les statistiques de régression supplémentaires et le tableau renvoyé est: {mn; mn-1; …; m1; b. sen; sen-1; …; sel; Seb. r2; sey.F; df.ssreg; ssresid}.
– Si Stats est FALSE ou non spécifié, la fonction LINEST () ne renvoie que les m-coefficients et la constante b.
Le tableau décrit les statistiques de régression supplémentaires.
| Statistique | Description |
| se1,se2,…,sen | Les valeurs d’erreur type correspondant aux coefficients m1,m2,…,mn. |
| Seb | La valeur d’erreur type correspondant à la constante b (seb = #N/A si l’argument constante a la valeur FAUX). |
| r2 | Le coefficient de détermination. Compare les valeurs y estimées aux valeurs y réelles et varie entre 0 et 1. Un coefficient de détermination égal à 1 indique une corrélation parfaite de l’échantillon (aucune différence entre les valeurs y estimées et réelles). A l’inverse, un coefficient de détermination égal à 0 (zéro) indique que l’équation de régression ne peut servir à prévoir une valeur y. Pour plus d’informations sur le mode de calcul de r2, consultez la section « Notes », plus loin dans cette rubrique. |
| Sey | L’erreur type pour la valeur y estimée. |
| F | La statistique F ou valeur F observée. Utilisez ce paramètre pour déterminer si la relation observée entre les variables dépendantes et indépendantes est due au hasard. |
| Df | Les degrés de liberté. Ils vous aident à trouver les valeurs critiques de la statistique F dans une table statistique. Comparez les valeurs trouvées dans la table à la statistique F renvoyée par la fonction DROITEREG pour déterminer le niveau de confiance du modèle. Pour plus d’informations sur le mode de calcul de df, consultez les « Remarques » plus loin dans cette rubrique. L’exemple 4 ci-dessous illustre l’utilisation de F et df. |
| Ssreg | La somme de régression des carrés. |
| Ssresid | La somme résiduelle des carrés. Pour plus d’informations sur le mode de calcul de ssreg et de ssresid, consultez les « Notes » plus loin dans cette rubrique. |
L’équation pour une ligne droite est y = mx + b. Lorsque vous connaissez les valeurs de m et b, vous pouvez calculer n’importe quel point de la ligne en insérant la valeur y ou la valeur x dans l’équation. Vous pouvez également utiliser la fonction TENDENCE ().
Contexte.
La corrélation examine si les variables sont liées entre elles et exprime cette relation avec un seul nombre. L’analyse de régression compare les variables dépendantes (par exemple, les commandes en ligne dans l’exemple de la société de logiciels) avec les variables indépendantes (les visites de sites Web).
Une analyse de régression est utilisée pour expliquer une caractéristique avec une caractéristique (variable dépendante) avec une ou plusieurs autres caractéristiques (variables indépendantes). On suppose que la variable dépendante augmente ou diminue en fonction de la variable indépendante.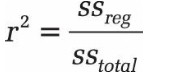 
Par conséquent, il détermine une dépendance unilatérale. Vous devez spécifier laquelle des deux variables est dépendante ou indépendante.
S’il n’existe qu’une seule variable x indépendante, vous pouvez calculer la pente et l’ordonnée à l’origine avec la formule suivante:
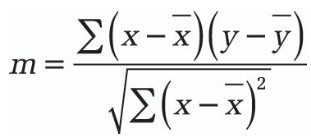
■ Pente: = INDEX (DROITEREG (y_connus; x_connus); 1)
■ y intercept: = INDEX (DROITEREG (y_connus; x_connus); 2)
La précision d’une ligne calculée avec DROITEREG () dépend de la variance des données. Plus les données sont linéaires, plus le modèle calculé par DROITEREG () est précis. DROITEREG () utilise les plus petits carrés pour calculer le meilleur ajustement pour les données. S’il n’existe qu’une seule variable x indépendante, calculez m et b avec la formule suivante:
Les valeurs x et y sont les moyennes des échantillons: x = MOYENNE (x_connus) et y =
MOYENNE (y_connus).
Les fonctions de régression DROITEREG () (régression linéaire) et LOGREG () (régression exponentielle) calculent le coefficient de la droite optimale en fonction des données fournies. Cependant, vous devez décider lequel des deux résultats correspond le mieux à vos données.
Dans une analyse de régression, Excel calcule le carré de la différence pour chaque point entre la valeur y d’un point et la valeur y réelle. La somme des différences au carré s’appelle une somme résiduelle de carrés (ssresid). Ensuite, Excel calcule la somme totale des carrés (sstotal). Si const = VRAI ou non spécifié, la somme totale des carrés est égale à la somme des différences au carré entre les valeurs de y réelles et la moyenne des valeurs de y. Si const = FAUX, la somme totale des carrés est égale à la somme des carrés des valeurs y réelles.
La somme des carrés de régression (ssreg) est calculée comme suit: ssreg = sstotal – ssresid
Plus la somme des carrés résiduels est petite par rapport à la somme totale des carrés d’écart, plus la valeur du coefficient de détermination (r2) est grande, ce qui indique dans quelle mesure la relation entre les variables est définie par l’équation résultant de la régression une analyse.
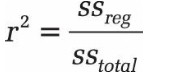
Parfois, une ou plusieurs colonnes x (en supposant que les valeurs x et y soient spécifiées dans des colonnes) ne sont pas utiles pour calculer les valeurs estimées avec les autres colonnes x. En d’autres termes, si vous excluez ces x colonnes, les valeurs y sont toujours exactes.
Dans ce cas, vous devez supprimer les x colonnes redondantes du modèle de régression. Ce phénomène est appelé colinéarité car chaque colonne x redondante peut être définie comme la somme du multiple des x colonnes non redondantes. LINEST () vérifie la colinéarité et exclut toutes les colonnes x redondantes du modèle de régression.
Dans la sortie de la fonction LINEST (), le coefficient et les valeurs propres d’une colonne x exclue sont égaux à 0. L’exclusion d’une ou de plusieurs colonnes a une incidence sur la df car celle-ci dépend du nombre de x colonnes utilisées pour calculer la valeur estimée. valeurs. Si la valeur de df change parce que les colonnes x redondantes sont supprimées, les valeurs de sey et de f sont également affectées. La colinéarité ne se produit pas très souvent.
Si aucune colonne x n’est exclue, le df est calculé comme suit: Si k colonnes existent et const = VRAI ou non spécifié:
df = n – k – 1
Si const = FALSE:
df = n – k
Dans les deux cas, pour chaque colonne x exclue, le df est augmenté de 1.
Si vous spécifiez une constante de tableau (telle que valuesx) en tant qu’argument, vous devez diviser les valeurs d’une ligne avec des deux points et les lignes avec des virgules.
–
Notez que si vous utilisez une équation de régression, les valeurs y prédites peuvent ne pas être valides car elles résident en dehors de la plage de valeurs y utilisée pour l’équation.
Exemple. Un éditeur de logiciels vend tous ses produits sur son site Web. La société envoie régulièrement des lettres d’information pour informer les clients existants et potentiels des nouveaux produits mis à jour et pour attirer l’attention sur son site Web.
L’année dernière, les commandes sur le site Web ont considérablement augmenté. La direction veut savoir la raison. L’augmentation des ventes est-elle attribuable au marketing ou à la publicité? L’augmentation des visites sur le site Web a-t-elle entraîné l’augmentation des ventes? Cela signifie que l’entreprise souhaite connaître la corrélation entre les visites sur le site Web et les commandes en ligne. Le responsable du site Web vous a fourni des informations sur les utilisateurs et leurs activités. Le service marketing est invité à effectuer une analyse et crée une liste Excel permettant de comparer les visites sur le site Web et les commandes en ligne des 18 derniers mois. Le service marketing effectue une analyse de régression à l’aide de la fonction LINEST () (voir Figure )
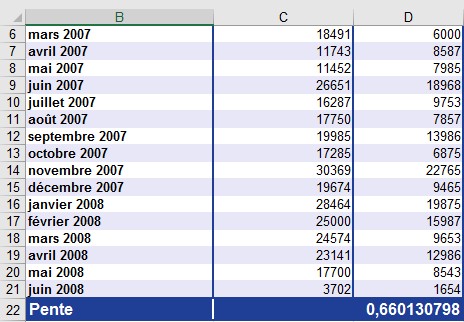
Figure Comparer les visites sur le site avec les commandes en ligne.
La figure montre comment la fonction LINEST () renvoie les résultats.