Syntaxe.
FISHER (x)
Définition.
Cette fonction renvoie la transformation de Fisher pour x. Cette transformation produit une fonction normalement distribuée avec une asymétrie d’environ 0. Utilisez cette fonction pour tester l’hypothèse du coefficient de corrélation.
Arguments
■ x (obligatoire). La valeur numérique que vous voulez transformer
REMARQUE
Si x n’est pas une valeur numérique, la fonction FISHER () renvoie le #VALUE! Erreur. Si x est inférieur ou égal à -1 ou supérieur ou égal à 1, la fonction FISHER () renvoie le #NUM! Erreur.
Contexte. Alors que la régression décrit le type et la covariance de la corrélation entre deux caractéristiques, la corrélation est le terme correspondant à leur relation.
Vous trouverez ci-dessous un aperçu de la corrélation produit-moment (Pearson):
■ La corrélation décrit la corrélation linéaire de deux variables.
■ La corrélation est la covariance normalisée ou la covariance.
■ La corrélation ne change pas avec la transformation linéaire des valeurs.
■ Le coefficient de corrélation r a des valeurs comprises entre -1 et +1 et une limite bilatérale.
■ Le coefficient est calculé pour les variables à échelle d’intervalle.
■ Le coefficient dépend de la variance des deux caractéristiques.
■ Une relation de cause à effet ne peut être dérivée d’une corrélation.
La transformation de Fisher (transformation z de Fisher) a été mise au point par Sir Ronald Aylmer Fisher (1890-1962), l’un des généticiens, modeleurs de l’évolution et statisticiens les plus renommés du XXe siècle.
Ce type de transformation a été développé pour établir des corrélations moyennes. Parce que le coefficient de corrélation n’est pas à l’échelle d’un intervalle, c’est-à-dire que la distance entre r = 0,20 et r = 0,40 n’est pas identique à la distance entre r = 0,40 et r = 0,60, la moyenne entre différentes corrélations ne peut pas être calculée. .
La solution est la transformation de Fisher, qui convertit les corrélations en variables à échelle d’intervalle. La moyenne des corrélations multiples est calculée comme suit:
- 1. Convertissez tous les coefficients de corrélation à moyenner en valeurs de Fisher.
- 2. Moyenne les valeurs z.
- 3. Retransformez les valeurs z moyennes en coefficients de corrélation
La valeur transformée peut être calculée avec la fonction FISHER () ou générée avec le code suivant.
formule: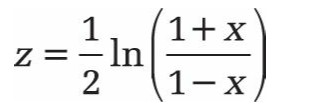
La transformation z transforme le coefficient de corrélation dans sa plage de valeurs (-1 à +1) en une distribution approximativement normale, c’est-à-dire que le coefficient de corrélation est asymptotique normal distribué pour effectuer des tests basés sur la distribution normale. Cela inclut les calculs de signification.
La formule pour la valeur attendue et la variance du coefficient de corrélation transformé en z est la suivante:
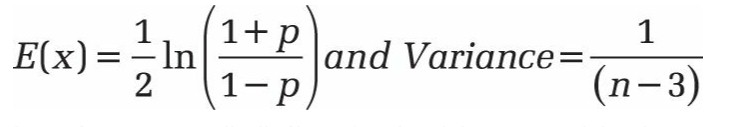
Exemple.
Une société de logiciels vend tous ses produits sur son site Web. La société envoie régulièrement des lettres d’information pour informer les clients existants et potentiels des nouveaux produits mis à jour et pour attirer l’attention sur son site Web. La société a été fondée en 2005. Le service marketing souhaite analyser les visites sur le site Web ainsi que les commandes en ligne des quatre dernières années afin de déterminer la dépendance entre les commandes et les visites sur le site Web. Vous avez déjà calculé le coefficient de corrélation pour chaque année afin de voir la corrélation entre les deux variables (voir la figure).
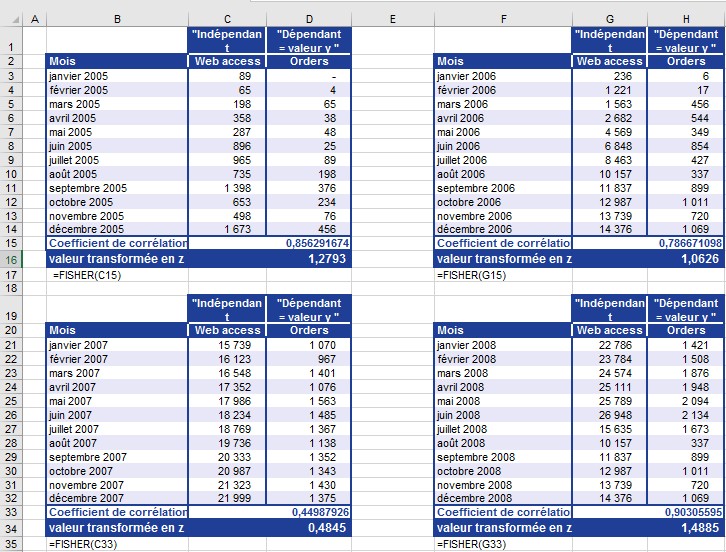
Maintenant, vous voulez calculer la corrélation moyenne pour les quatre dernières années. Comme le coefficient de corrélation n’est pas à l’échelle d’intervalle, vous ne pouvez pas calculer la moyenne à partir de différentes corrélations.
Par conséquent, vous utilisez la fonction FISHER () pour transformer tous les coefficients de corrélation en valeurs Fisher. Vous spécifiez le coefficient de corrélation pour l’argument x de la fonction FISHER ().
La figure montre le résultat du calcul avec la fonction FISHER ().
Pour retransformer la moyenne calculée à partir des valeurs z en un coefficient de corrélation, utilisez la fonction FISHERINV ().
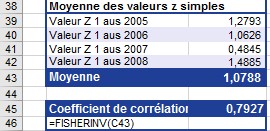
Vous devez retransformer la moyenne calculée en un coefficient de corrélation pour obtenir la corrélation entre les visites sur le site Web et les commandes en ligne des quatre dernières années. Comme vous pouvez le voir sur la figure , le coefficient de corrélation calculé à partir de la moyenne est de 0,7927.
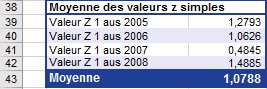
Figure . Transformer la moyenne (calculer à partir des valeurs z) en un coefficient de corrélation.
Pour retransformer la moyenne calculée à partir des valeurs z en un coefficient de corrélation, utilisez la fonction FISHERINV ().
Vous devez retransformer la moyenne calculée en un coefficient de corrélation pour obtenir la corrélation entre les visites sur le site Web et les commandes en ligne des quatre dernières années. Comme vous pouvez le voir sur la figure , le coefficient de corrélation calculé à partir de la moyenne est de 0,7927.
Les déclarations suivantes peuvent être faites:
■ Le coefficient de corrélation de 0,7927 indique une corrélation positive. Plus le coefficient de corrélation est proche de 1, plus la corrélation est proche. Cela signifie que les visites sur le site Web et les commandes en ligne sont interdépendantes linéaires.
■ Si le nombre de visites sur le site Web augmente en raison d’activités de marketing, le nombre de commandes en ligne augmente également.
■ Cela prouve qu’au cours des quatre dernières années, les commandes en ligne ont été tributaires du nombre de visites sur le site Web.
