Syntaxe.
INTERET.ACC (émission; prem_coupon; règlement; taux; val_nominale; fréquence; [base]; [méth_calcul]
Définition.
La fonction INTERET.ACC () calcule les intérêts courus d’une dette échue intégralement chaque année ou les intérêts courus d’un titre à intérêt fixe avec des paiements d’intérêts périodiques.
Arguments
■ Émission (obligatoire) Spécifie la date de l’accord de prêt ou de l’émission du titre.
■ prem_coupon (requis) Identique à la date d’échéance si elle est intra-annuelle; sinon, résulte du nombre de périodes, qui est défini par la fréquence.
■ Règlement (obligatoire) Date à laquelle la propriété du titre a changé.
■ taux(obligatoire) Taux d’intérêt annuel convenu (taux d’intérêt du coupon) du titre de créance / du prêt / de l’obligation.
■ Valeur nominale (facultatif) Valeur nominale de la sécurité. Si cet argument n’est pas spécifié, Excel calcule avec 1 000 unités monétaires (contrairement aux informations fournies dans l’aide d’Excel dans Excel 2003 et les versions antérieures).
■ Fréquence (obligatoire) Spécifie le nombre de paiements d’intérêts au cours d’une année. Les valeurs valides sont les entiers 1 = annuel; 2 = semestriel; 4 = trimestriel.
■ Base (facultatif) Définit la méthode à utiliser pour déterminer les jours de l’année selon le tableau 15-2, présenté dans la section intitulée AMORDEGRC (). Si cet argument est omis, Excel calcule avec Basis = 0.
■ Méthode de calcul (facultatif) Valeur logique qui détermine si les intérêts sont calculés pour la durée jusqu’à ce point (VRAI ou omis) ou si seul l’intérêt depuis le dernier paiement d’intérêts est spécifié (FAUX).
Tous les arguments de fonction qui appellent une date utilisent la date sans l’heure. En d’autres termes, les fractions sont arrondies. Les arguments Fréquence et Base nécessitent également des entiers et des décimales tronquées.
Si des dates non valides sont utilisées ou si aucun nombre n’est entré, le cas échéant, la fonction renvoie l’erreur #VALUE!. Si des nombres non valides sont entrés pour des arguments sans date, la fonction renvoie le #NUMBER! Erreur.
Contexte.
Les intérêts des emprunts / obligations à taux fixe sont payés une ou plusieurs fois par an en fonction de l’argument Fréquence. Si le titre change de propriété entre les délais d’intérêts, l’acheteur doit payer au vendeur le taux d’intérêt ainsi que les intérêts courus jusqu’à cette date (qui constitue le prix d’achat). S’il y a plus d’une date d’intérêt dans l’année, les intérêts courus sont
calculé en divisant l’intérêt nominal par le nombre de dates d’intérêt. Avec ce taux d’intérêt (relatif), les jours de la période d’intérêt de départ sont ensuite calculés à l’aide de la méthode de comptage de jours spécifiée dans l’argument de base.
Exemple.
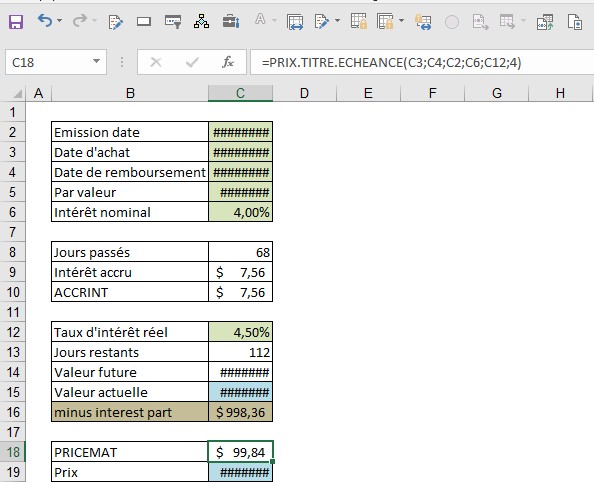
Une dette de 1 000,00 $, due intégralement avec un taux d’intérêt nominal de 4% par an. et un remboursement au plus tard le 1er décembre 2010 a été convenu le 1er juin 2010. Le 9 août 2010, les créanciers changent. À cette date, un taux d’intérêt réel de 4,5% par an. pour le temps restant jusqu’au remboursement est habituel. Quel prix la personne qui prend en charge la dette paie-t-elle?
Pour en venir au fait tout de suite: vous pouvez simplement déterminer le résultat avec les fonctions PRIX.TITRE.ECHEANCE () et INTERET.ACC (). Toutefois, si vous souhaitez recréer ce que ces fonctions font, réfléchissez aux points suivants:
■ Combien d’intérêts ont été accumulés jusqu’à aujourd’hui et doivent être payés au créancier? La réponse de 7,56 $ (après avoir arrondi) est
= ACCRINT (C2; C4; C3; 4%; 1000; 1; 4)
si la cellule C2 contient la date du 1er juin 2010; C3 la date du 9 août 2010; et C4 la date du 1er décembre 2010. Vous pouvez le vérifier en comptant les jours écoulés depuis le contrat d’endettement (68 ans, comme le prouvent également JOURS360 () et NB.JOURS.COUPON.PREC ()) et en déterminant la partie intérêts avec
1000 * 68/360 * 4%.
■ Quelle est la valeur du décaissement de 1 000,00 $ plus les intérêts (de 4% / 2 pour 1 000, en raison de la différence d’un semestre seulement) le 1er décembre 2010, avec le taux d’intérêt réel donné le 9 août 2010? Cela est calculé en actualisant la valeur future de 1 020,00 $ jusqu’au 9 août 2010. Pour ce faire, vous pouvez déterminer qu’il reste 112 jours (avec Base = 4) entre les deux dates. DAYS360 () peut aider ici, de même que la fonction COUPDAYSNC (), qui reconnaît les compteurs autres que 30/360 jours. La valeur de rachat est de 1 005,92 $.
■ Vous obtenez la même valeur en espèces (prix) si vous multipliez le résultat de PRIX.TITRE.ECHEANCE () par 10, puis ajoutez les intérêts courus. Une multiplication par 10 est nécessaire car PRIX.TITRE.ECHEANCE () utilise une valeur nominale de 100.