Syntaxe.
INVERSE.LOI.F.DROITE (probabilité; degrés _ liberté1; degrés _ liberté2)
Définition.
La fonction INVERSE.LOI.F.DROITE () renvoie l’inverse de la distribution F droite. Si p = FDIST.RT (x, …) alors INVERSE.LOI.F.DROITE (p, …) = x.
La distribution F peut être utilisée dans un test f pour comparer les variances dans deux ensembles de données. Par exemple, vous pouvez analyser les distributions de revenus aux États-Unis et au Canada pour déterminer si les deux pays ont une diversité de revenus similaire.
Arguments
■ probabilité (obligatoire). La probabilité associée à la distribution F
■ degrés_liberté1 (obligatoire). Les degrés de liberté au numérateur
■ degrés_liberté2 (obligatoire). Les degrés de liberté au dénominateur
Contexte.
Comme mentionné précédemment, le résultat d’un calcul ANOVA comprend souvent des données pour la statistique F, la probabilité F et la valeur F critique au niveau de signification de 0,05. Cette fonction effectue une analyse de variance simple pour évaluer l’hypothèse selon laquelle les moyennes de deux échantillons ou plus sont égales. La fonction peut également tester l’importance des différences dans les moyennes arithmétiques de ces groupes pour vérifier si la variance entre les moyennes est aléatoire.
La fonction INVERSE.LOI.F.DROITE () calcule la valeur critique d’une distribution. Pour calculer la valeur critique, transmettez le niveau de signification comme argument de probabilité à INVERSE.LOI.F.DROITE ().
Le calcul de INVERSE.LOI.F.DROITE () vous permet de tirer une conclusion concernant l’hypothèse nulle. Les arguments de la fonction INVERSE.LOI.F.DROITE () sont des probabilités (par exemple, niveau de signification a),
degrés_liberté1 et degrés_liberté2.
Exemple.
Vous travaillez en tant qu’ergothérapeute et souhaitez savoir dans quelle mesure les employés s’identifient à une entreprise. Vous avez sélectionné 15 employés. Chaque employé a répondu à 10 questions sur d’autres sujets. Pour chaque question, les employés pouvaient choisir entre trois réponses.
Vous avez déjà résumé les réponses (voir la figure).
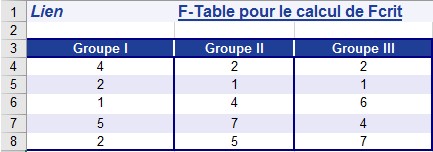

Figure. Les résultats de l’enquête.
L’hypothèse nulle est qu’il n’y a pas de différence entre les trois groupes. L’hypothèse alternative suppose le contraire. Le niveau de signification est de 0,05%. La figure montre le résultat de l’analyse de variance univariée.

Figure Calcul de l’analyse de variance univariée et de la valeur critique de F.
Le résultat distingue les différences entre les groupes et les différences au sein des groupes, car non seulement les trois groupes sont différents, mais les résultats des employés d’un groupe sont également différents.
Les différences entre les groupes correspondent à la différence évaluée et les différences au sein d’un groupe sont aléatoires.
Le nombre de degrés de liberté 1 (degrés de liberté au sein des groupes) est calculé en fonction de la taille des trois groupes moins 1 (5 – 1 + 5 – 1 + 5 – 1 = 12). Le nombre de degrés de liberté 2 (degrés de liberté entre les groupes) est calculé sur la base du nombre de groupes moins 1 (3 – 1 = 2).
