Syntaxe.
LOI.BINOMIAL.NEG.N (nombre_f, nombre_s, probabilité_s)
Définition.
Cette fonction renvoie les probabilités d’une variable aléatoire distribuée binomiale négative.
LOI.BINOMIAL.NEG.N () calcule la probabilité qu’il y ait des échecs number_f avant le dernier nombre_s lorsque la probabilité constante de réussite est probabilités_s.
Arguments
number_f (obligatoire). Le nombre d’échecs
number_s (obligatoire). Le nombre de succès
probabilité_s (obligatoire). La probabilité de réussite
REMARQUE
Number_f et number_s sont tronqués en entiers. Si l’un des arguments n’est pas une expression numérique,LOI.BINOMIAL.NEG.N ()
la fonction retourne le #VALUE! Erreur.
Si probabilité_s est inférieure à 0 ou supérieure à 1, la fonction LOI.BINOMIAL.NEG.N () renvoie le #NUM! Erreur.
Si number_f est inférieur à 0 ou number_s est inférieur à 1, la fonction LOI.BINOMIAL.NEG.N () renvoie le #NUM! Erreur.
Contexte. Cette fonction est similaire à la distribution binomiale, sauf que le nombre de réussites est fixe et le nombre d’essais est variable. Ceci s’appelle une distribution binomiale négative. Comme avec
Dans la distribution binomiale, les essais sont supposés être indépendants.
Dans une expérience aléatoire avec des répétitions indépendantes et seulement deux résultats possibles (succès ou échec), la distribution binomiale négative (ou distribution Pascal) renvoie la probabilité d’un problème fixe.
nombre d’échecs avant le xième succès. L’équation pour une distribution binomiale négative est

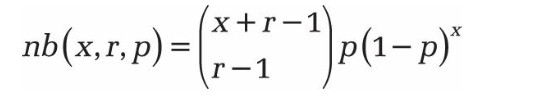
où
x est égal à number_f
r est égal à number_s
p est égal à probabilité
Exemple.
Vous êtes en vacances dans une ville étrangère et demandez conseil à un passant. Cette question ne peut être répondue que par oui ou non. Cela signifie qu’il existe une probabilité de 50% que la réponse
est oui. Par conséquent, p est 0.5.
Une fois que vous avez demandé à quelques personnes et que personne ne peut vous dire le chemin, vous achetez une carte. Maintenant, vous voulez savoir la probabilité que vous trouverez
Cinq personnes qui connaissent le chemin ou combien de réponses «Non, je suis désolé» vous obtiendrez avant de rencontrer cinq personnes qui connaissent le chemin. Vous calculez la probabilité avec la fonction LOI.BINOMIAL.NEG.N (), comme illustré à la figure .

Vous pouvez faire des déclarations suivantes à partir de ce résultat: Numéro du correspondant_f = 6 dans la Figure 12-101, la possibilité de demander à six personnes dont le chemin avant à demander à cinq personnes n’est 10,25 pour cent.