Définition.

Cette fonction renvoie les probabilités d’une variable aléatoire distribuée binomiale. Utilisez la fonction LOI.BINOMIALE() pour les problèmes avec un nombre déterminé de tests ou d’essais lorsque les résultats d’un essai ne sont que des succès ou des échecs, lorsque les essais sont indépendants et que la probabilité de succès est constante pendant tous les essais. Par exemple, vous pouvez utiliser la fonction LOI.BINOMIALE() pour calculer la probabilité que 50 personnes sur 100 dans un restaurant soient favorables à une interdiction de fumer.

Arguments

■ nombre_s (obligatoire). Le nombre de succès dans les essais.

■ essais (obligatoire). Le nombre d’essais indépendants.

■ probabilité_s (obligatoire). La probabilité de réussite de chaque essai.

■ cumulatif (obligatoire). La valeur logique qui représente le type de la fonction. Utilisez VRAI pour la distribution cumulative, sinon utilisez FAUX pour la distribution de masse de probabilité.

Contexte.

 En général, la probabilité peut être définie comme la probabilité qu’un événement se produise lors de l’exécution d’un essai aléatoire où aucun des événements donnés n’est privilégié.

Par exemple, quelle est la probabilité que 30 paquets soient endommagés lors de la production de 2000 pilules si on suppose que 2% des paquets seront endommagés?

Les essais aléatoires pour lesquels une variable aléatoire peut appartenir à l’une des deux catégories sont généralement appelés expériences de Bernoulli, du nom du mathématicien suisse Jakob Bernoulli (1654-1705).

La variable aléatoire (variable de Bernoulli) x a la valeur x=1 avec une probabilité p (succès) et la valeur X=0 avec une probabilité q=1-p (échec). La probabilité p est aussi appelée le taux de réussite.

Vous rencontrez souvent des événements où le résultat peut être divisé en deux catégories. Il existe donc une série d’expériences de Bernoulli. La probabilité que la variable aléatoire x=1 apparaisse dans k cas est calculée avec la formule de Bernoulli suivante:

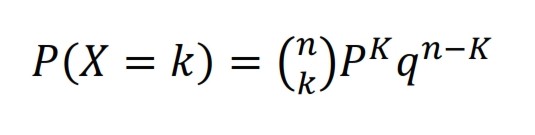
La distribution

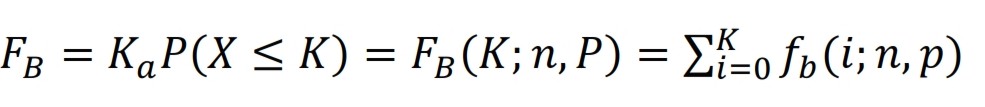
de la variable aléatoire est appelée distribution binomiale, avec le coefficient binomial

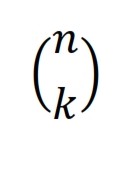
– c’est n sur k.

La distribution binomiale est l’une des distributions de probabilité les plus importantes et constitue un cas particulier des distributions multinomiales. La distribution binomiale décrit les résultats des processus de Bernoulli, définis à leur tour comme plusieurs expériences de Bernoulli conduites dans des conditions cohérentes (par exemple, le tirage au sort d’une pièce de monnaie).

Si vous lancez une pièce, la probabilité de succès et d’échec est la même. Cependant, si vous lancez la pièce 12 fois, vous obtenez 2¹² résultats possibles.

Exemple.

Le résultat de sept “têtes” signifie que sept des 12 résultats ont “têtes” en un seul résultat. Choisir sept objets sur 12 est possible à bien des égards:

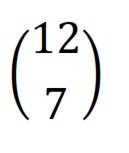
Par conséquent, la probabilité d’obtenir sept résultats de tête est égale à

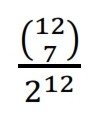
Excel fournit la fonction BINOM.DIST() pour calculer la probabilité d’une variable aléatoire distribuée binomiale. La figure montre un exemple de distribution binomiale.

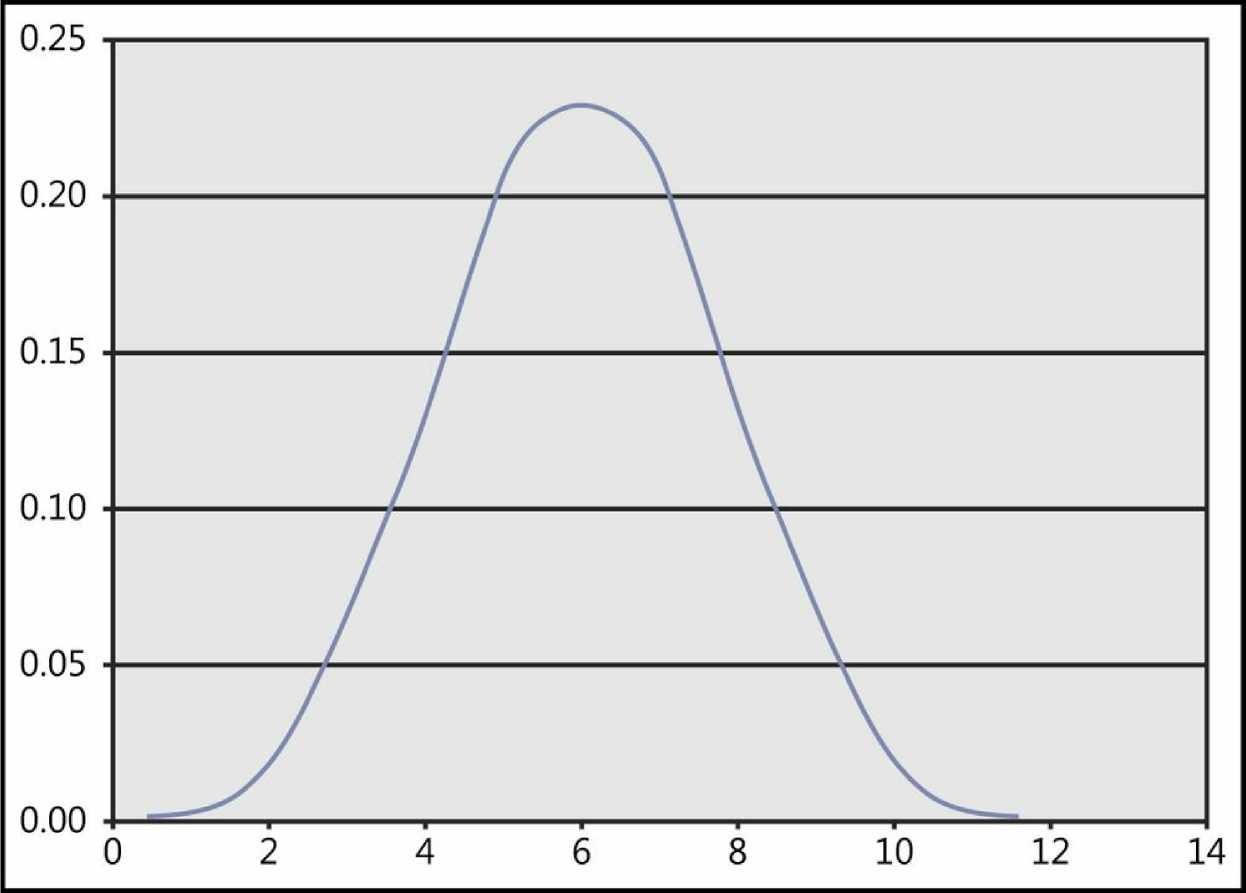
La fonction de densité de la distribution binomiale est

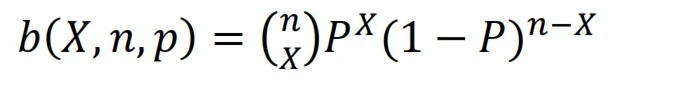
où

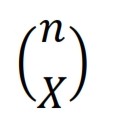
est COMBIN(n; x). La fonction de distribution de la distribution binomiale est 

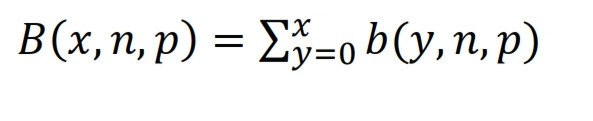
Exemples

Directions de vacances. Vous êtes en vacances dans une ville étrangère et demandez à un passant de vous indiquer comment vous y rendre. La question «Connais-tu le chemin?» Ne peut être répondue que par oui ou non. Cela signifie qu’il existe une probabilité de 50% que la réponse soit oui. Par conséquent, p est 0.5.
Vous voulez connaître la probabilité que 66 des 100 répondants (2/3) répondent par l’affirmative. La figure  montre le calcul de la probabilité pour la variable aléatoire distribuée binomiale 66.

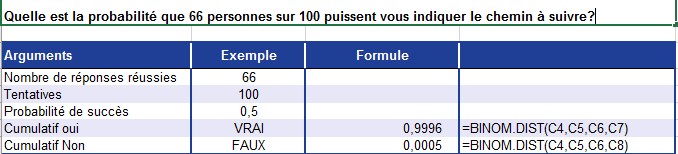
Figure . Calcul de la probabilité pour une variable aléatoire dist

ribuée binomiale.

Voici les résultats:
■ La probabilité que vous obteniez au maximum 66 réponses positives de 100 personnes interrogées est proche de 100%.
■ La probabilité que vous obteniez exactement 66 réponses positives de 100 personnes interrogées est de 0,05%.
De cette façon, vous pouvez calculer de nombreuses probabilités différentes.
Endommagés. Prenons l’exemple de la fonction LOI.BINOMIALE (). La question posée dans cet exemple était la suivante: quelle est la probabilité que 30 emballages soient endommagés lors de la production de 2 000 pilules si on suppose que 2% des emballages seront endommagés? La figure  montre le résultat.

LOI.BINOMIALE() renvoie la probabilité pour une variable aléatoire distribuée binomiale.

Voici ce que vous avez découvert:
■ La probabilité qu’un maximum de 30 paquets soit endommagé est de 6%.
■ La probabilité que exactement 30 paquets soient endommagés est de 1,8%.