Syntaxe.

  LOI.EXPONENTIELLE.N (x; lambda; cumulatif)

Définition.

Cette fonction renvoie les probabilités d’une variable aléatoire exponentielle distribuée. Utilisez LOI.EXPONENTIELLE.N  () pour modéliser le temps entre les événements. Par exemple, vous pouvez calculer la probabilité qu’un centre d’appels reçoive un appel après trois minutes, bien que la moyenne horaire pour les appels entrants soit de trois minutes.

Arguments

■ x (obligatoire). La valeur de la fonction.

■ lambda (obligatoire). La valeur qui est passée.

■ cumulatif (obligatoire). La valeur logique Si cumulative est VRAI, la distribution cumulative est renvoyée. sinon, la fonction de densité de probabilité est renvoyée.

Contexte.

Ces fonctions ont une caractéristique particulière: à intervalles égaux, la valeur de la fonction change du même facteur. Ces fonctions sont utiles pour décrire les processus de croissance et de décroissance pour lesquels la valeur change du même facteur à intervalles de temps égaux. Les fonctions inverses sont appelées logarithmes. La fonction exponentielle x = ex avec le nombre d’Euler e est la base (voir figure).

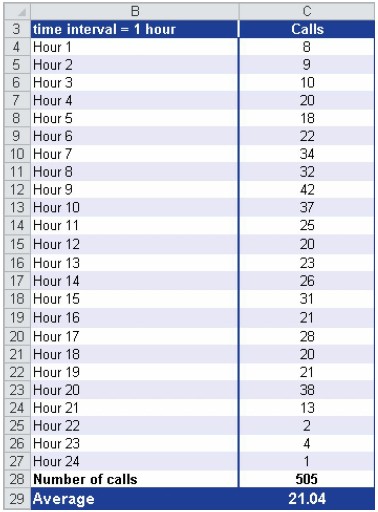
Comme indiqué précédemment, la fonction LOI.EXPONENTIELLE.N  () renvoie les probabilités d’événements indépendants, telles que le temps qu’il faut à un guichet automatique pour répartir de l’argent ou d’autres délais d’attente.

Voici un autre exemple: si un centre d’appels d’assistance reçoit un appel toutes les trois minutes, vous pouvez utiliser cette fonction pour calculer la probabilité que le téléphone sonne au bout d’une minute seulement. C’est ce qu’on appelle une variable aléatoire exponentielle, car la sonnerie du téléphone et l’heure sont indépendantes l’une de l’autre. La fonction LOI.EXPONENTIELLE.N  () calcule la probabilité que cela se produise.

L’équation de la densité de probabilité est la suivante:

f(x; λ) = λe^–λx

L’équation pour la fonction de distribution est la suivante:

F(x; λ) = 1 – e^–λx