Syntaxe.

LOI.F.DROITE  (x; degrés _ liberté1; degrés _ liberté2)

Définition.

Cette fonction renvoie les valeurs d’une fonction de distribution (1 alpha) d’une variable aléatoire droite distribuée par F. Utilisez cette fonction pour déterminer si deux ensembles de données présentent des variances différentes. Par exemple, vous pouvez comparer les résultats du sondage de trois groupes d’employés égaux pour déterminer si la variance ou les résultats sont différents.

Arguments

■ x (obligatoire). La valeur à laquelle évaluer la fonction

■ degrés_liberté1 (obligatoire). Les degrés de liberté au numérateur

■ degrés_liberté2 (obligatoire). Les degrés de liberté au dénominateur

REMARQUE
Si l’un des arguments n’est pas une valeur numérique, la fonction LOI.F.DROITE() renvoie le #VALUE! Erreur.
Si x est négatif, F.DIST.RT () renvoie le #NOM! valeur d’erreur.
Si degrés_liberté1 ou degrés_liberté2 n’est pas un entier, les décimales sont tronquées. Si degrés_liberté1 est inférieur à 1 ou degrés_liberté2 supérieur ou égal à 1010, la fonction renvoie le #NOMB! Erreur. Si degrés_libert2 est inférieur à 1 ou degrés_libert2 est supérieur ou égal à 1010, la fonction renvoie le #NOM! Erreur.
F.DIST.RT () est calculé comme suit: F.DIST.RT = P (F> x) où F est une variable aléatoire F-distribuée avec degrés_liberté1 et degrés_liberté2.

Contexte.

La fonction LOI.F.DROITE () renvoie le niveau de signification basé sur une valeur. La fonction LOI.F.DROITE RT () calcule la probabilité, c’est-à-dire le niveau de signification, des valeurs critiques calculées par F.INVRT ().

La fonction F.INVRT () calcule la valeur F critique en fonction de la probabilité et des degrés de liberté et requiert l’argument de probabilité.

Exemple.

Prenons l’exemple de INVERSE.LOI.F.DROITE (). Dans un sondage, 15 employés devaient répondre à 10 questions. Comme indiqué à la figure ,

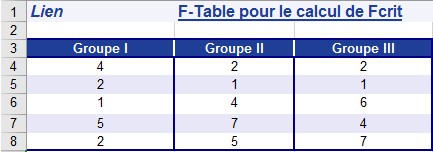
chaque question comportait trois réponses possibles.

L’hypothèse nulle indique qu’il n’y a pas de différence entre les trois groupes. Cependant, l’hypothèse alternative suppose le contraire. Une analyse de variance simple renvoie les résultats présentés dans la figure.

Avec la fonction INVERSE.LOI.F.DROIT () et un niveau de signification (probabilité) de 0,05, vous calculez une valeur F critique de 3,89. La fonction LOI.F.DROITE () renvoie un niveau de signification de 0,05.

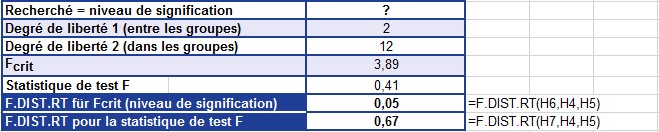
L’exemple utilise les valeurs indiquées dans la figure pour calculer LOI.F.DROITE ().

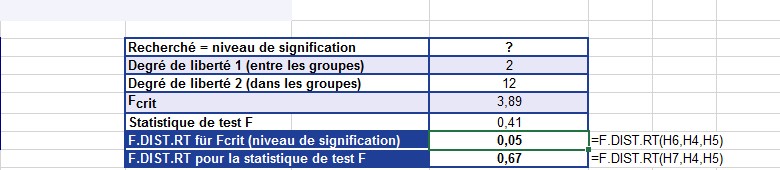
Le calcul du niveau de signification pour F renvoie le résultat présenté à la figure 12-44.

La fonction LOI.F.DROITE () renvoie une probabilité de 0,67 (67%) pour la statistique F = 0,4161 (voir la figure).

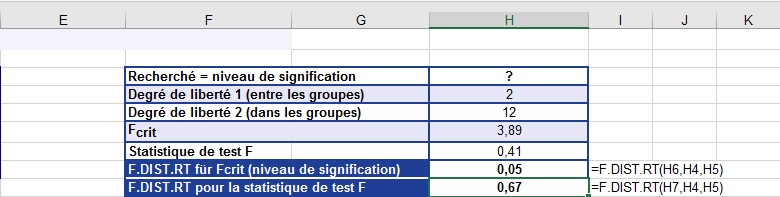
La figure LOI.F.DROITE ()renvoie le niveau de signification de la statistique F.

Comme le niveau de signification a est supérieur à la statistique F, l’hypothèse nulle est confirmée. Cela signifie que vous pouvez supposer qu’il n’y a pas de différence significative entre les deux groupes.