Syntaxe.

LOI.GAMMA (x;alpha; bêta; cumul)

 Définition.

Cette fonction renvoie les probabilités d’une variable aléatoire distribuée par un gamma. Utilisez ceci

fonction pour examiner les variables qui ont une distribution asymétrique. La distribution gamma est généralement utilisé dans les analyses de file d’attente.

Arguments

■ x (obligatoire). La valeur (quantile) pour laquelle vous voulez calculer la probabilité (1-alpha).

■ alpha (obligatoire). Un paramètre de la distribution.

■ beta (obligatoire). Un paramètre de la distribution. Si beta = 1, LOI.GAMMA () renvoie la distribution gamma standard.

■ cumulatif (obligatoire). La valeur logique qui représente le type de la fonction. Si cumulative vaut VRAI, LOI.GAMMA () renvoie la valeur de la fonction de distribution, c’est-à-dire la probabilité que le nombre d’événements aléatoires soit compris entre 0 et x. Si cumulative vaut FAUX, la fonction LOI.GAMMA () renvoie la valeur de la fonction de densité.

REMARQUE

Si x alpha ou bêta n’est pas une expression numerica, la fonction GAMMA.DIST () renvoie la valeur Valeur! Erreur
Si x est inférieur à O, la fonction renvoie le ⋕NUM! Erreur

La fonction de densité pour la distribution gamma standard

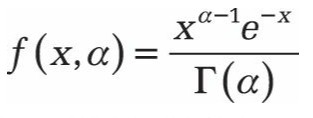
Si alpha = 1, GAMMA.DIST () renvoie la distribution exponentielle avec les éléments suivants:

■ Si alpha est un entier positif, la distribution gamma est également appelée distribution Erlang.

■ Pour un entier positif n, lorsque alpha = n / 2, bêta = 2 et cumulatif = VRAI, GAMMA.DIST () renvoie le même résultat que (1 CHIDIST (x)) avec n degrés de liberté.

Contexte.

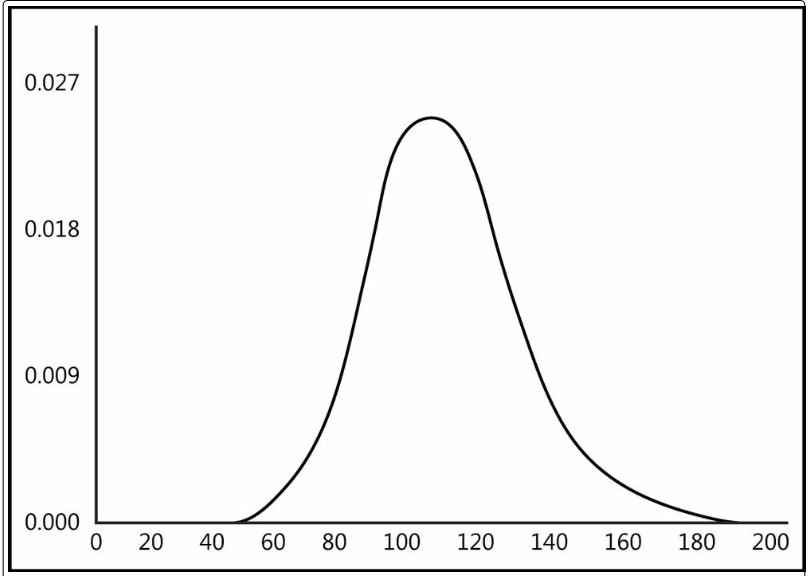
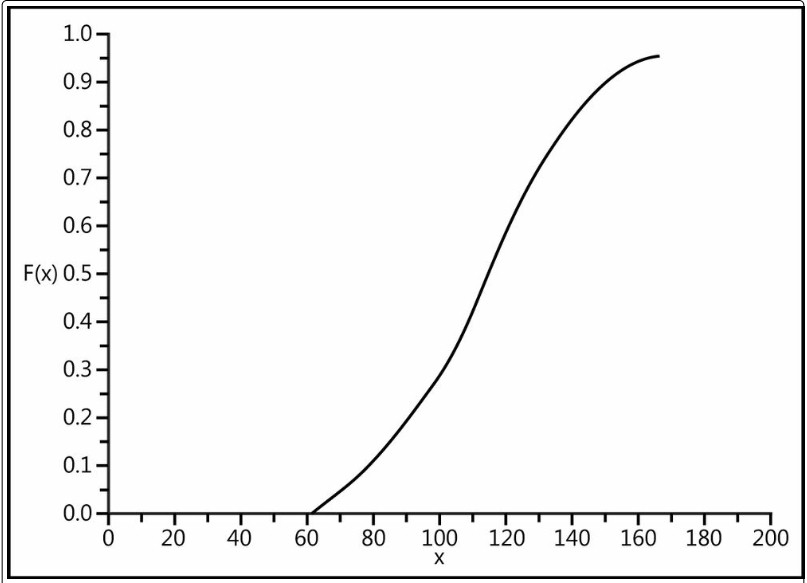
La distribution gamma est une distribution de probabilité continue de vrais réels

chiffres (voir la figure). La distribution gamma est définie par la densité de probabilité avec x

supérieur à 0.

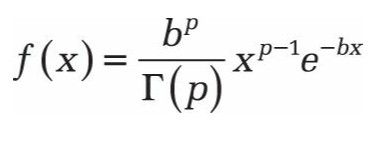
Pour les autres valeurs, la fonction de densité gamma est poursuivie avec f (x) = 0. Les paramètres sont p et q (alpha et bêta). Pour assurer la normalisationp, q doit être supérieur à 0. Le préfacteur bp / r (p) vérifie que la normalisation est correcte. L’expression r (p) est la fonction gamma.

Le tableau suivant montre la valeur et la variance attendues de la distribution gamma:

La distribution gamma est reproductrice.

La somme des variables aléatoires x et y stochastiquement indépendantes, gamma-distribuées avec les paramètres b and px ou py, est gamma-distribuée avec les paramètres b and px + py.

La distribution gamma crée une famille pour plusieurs fonctions de distribution théoriques:

■ La distribution du khi-carré à k degrés de liberté est une distribution gamma utilisant les paramètres p = k / 2 et b =! 4

■ La distribution exponentielle avec le paramètre X est une distribution gamma utilisant les paramètres p = 1 et b = X. Selon celle-ci, la distribution d’Erlang avec le paramètre X et n degrés de liberté correspond à une distribution gamma avec les paramètres p = n et b = X.

■ Le quotient X / (X + Y) issu des variables aléatoires stochastiquement indépendantes x et y gamma- réparties avec les paramètres b and px ou py est distribué avec les paramètres px et py.

Alternativement,

les paramètres sont les suivants:

La densité et les moments sont modifiés en conséquence (par exemple, la valeur attendue serait aP). Du fait que ce paramétrage est couramment utilisé dans le monde anglophone, on peut souvent le trouver dans la littérature technique. Pour éviter les malentendus, il est recommandé de spécifier explicitement les moments (par exemple, la valeur attendue ab et la variance ab2) pour une distribution gamma (voir la figure).

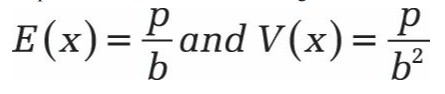
La distribution gamma est reproductrice.
La somme des variables aléatoires x et y stochastiquement indépendantes, gamma-réparties avec les paramètres b andpx ou py, est gamma-répartie avec les paramètres b et px + py.
La distribution gamma crée une famille pour plusieurs fonctions de distribution théoriques:
■ La distribution du khi-carré à k degrés de liberté est une distribution gamma utilisant les paramètres p = k / 2 et b =! 4
■ La distribution exponentielle avec le paramètre X est une distribution gamma utilisant les paramètres p = 1 et b = X. Selon celle-ci, la distribution Erlang avec le paramètre X et n degrés de liberté correspond à une distribution gamma avec les paramètres p = n et b = X.
■ Le quotient X / (X + Y) issu des variables aléatoires stochastiquement indépendantes x et y gamma- distribuées avec les paramètres b andpx ou py est bêta-distribué avec les paramètres px et py.
Alternativement, les paramètres sont les suivants:

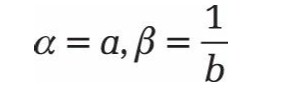
La densité et les moments sont modifiés en conséquence (par exemple, la valeur attendue serait aP). Du fait que ce paramétrage est couramment utilisé dans le monde anglophone, on peut souvent le trouver dans la littérature technique. Pour éviter les malentendus, il est recommandé de spécifier explicitement les moments (par exemple, la valeur attendue ab et la variance ab2) pour une distribution gamma (voir la figure ).

La fonction LOI.GAMMA () est une faction de distribution mathématique à deux paramètres (alpha et beta) basée sur la fonction gamma. LOI.GAMMA () est la fonction inverse de GAMMA.INV

Exemple. Utilisez les valeurs suivantes pour calculer LOI.GAMMA ():

■ 10 = valeur (quantile) pour laquelle vous voulez calculer la probabilité

■ 2,70 = paramètre alpha de la distribution

■ 2 = paramètre bêta de la distribution

La figure illustre le calcul de LOI.GAMMA ().

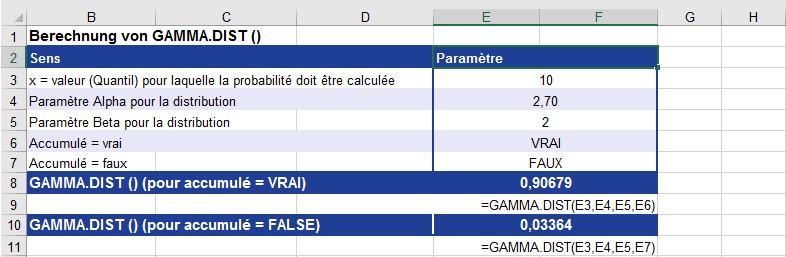
Avec les paramètres illustrés à la figure 12-42, la fonction GAMMA.DIST () renvoie les résultats suivants:
■ 0,90679 = probabilité de la distribution gamma sur la base des données fournies et cumulative = VRAI
■ 0,03364 = probabilité de la distribution gamma basée sur les données fournies et cumulative = FALSE