Syntaxe.
LOI.GAMMA.INVERSE (probabilité;alpha;bêta)
Définition.
Cette fonction renvoie le quantile de la distribution gamma. Si p = LOI.GAMMA (x, …), alors LOI.GAMMA.INVERSE (pv ..) = x.
Utilisez cette fonction pour examiner une variable dont la distribution peut être asymétrique.
Arguments
■ probabilité (obligatoire). Une probabilité associée à la distribution gamma.
■ alpha (obligatoire). Un paramètre de la distribution.
■ beta (obligatoire). Un paramètre de la distribution. Si beta = 1, LOI.GAMMA.INVERSE () renvoie la distribution gamma standard.
REMARQUE
Si l’un des arguments n’est pas une expression numérique, la fonction LOI.GAMMA.INVERSE () renvoie le #VALUE! Erreur.
Si la probabilité est inférieure à 0 ou supérieure à 1, la fonction LOI.GAMMA.INVERSE () renvoie le #NUM! Erreur.
Si alpha ou bêta est inférieur ou égal à 0, la fonction LOI.GAMMA.INVERSE () renvoie le #NUM! Erreur.
Si la probabilité a une valeur, LOI.GAMMA.INVERSE () recherche la valeur x afin que GAMMA.DIST (x, alpha, bêta, VRAI) = probabilité. Par conséquent, la précision de LOI.GAMMA.INVERSE () dépend de celle de LOI.GAMMA.INVERSE (). GAMMA.INV () utilise une technique de recherche itérative. Si la recherche n’a pas convergé après 100 itérations, la fonction renvoie l’erreur # N / A.
Contexte.
LOI.GAMMA.INVERSE () est la fonction inverse de LOI.GAMMA () et peut être utilisé pour surveiller une distribution gamma. Les arguments alpha et beta correspondent aux valeurs de la fonction GAMMA.DIST (). La probabilité peut être n’importe quelle valeur comprise entre 0 et 100%. LOI.GAMMA () calcule la position de x sur l’axe horizontal qui correspond au rapport de surface cumulé de la distribution gamma.
Exemple.
Utilisez les valeurs de la figure pour calculer LOI.GAMMA.INVERSE. La figure montre également le calcul de GAMMA.INV ().
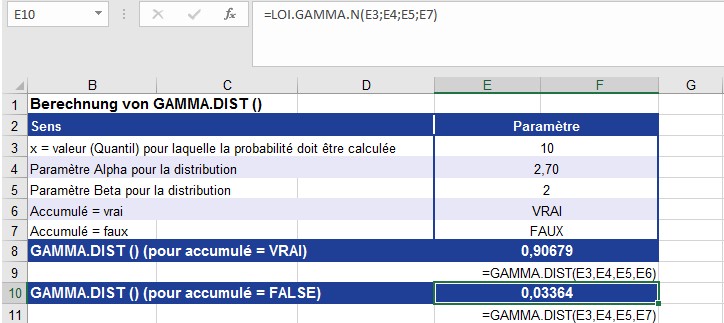
La fonction GAMMA.INV () renvoie le quantile 10 pour la distribution gamma en fonction des paramètres affichés.
