LOI.LOGNORMALE.N (x; moyenne; écart_type; cumulative)

 Définition.

Cette fonction renvoie les valeurs de la fonction de distribution d’une variable aléatoire distribuée lognormale où ln (x) est normalement distribué avec les paramètres moyenne et écart_type. Utilisez cette fonction pour analyser des données transformées de manière logarithmique.

Arguments

■ x (obligatoire). La valeur à laquelle évaluer la fonction

■ moyen (obligatoire). La moyenne de la distribution log-normale

■ écart_type (obligatoire). L’écart-type de la distribution log-normale

■ cumulatif (obligatoire). La valeur logique qui représente le type de la fonction

Contexte.

La fonction LOI.LOGNORMALE.N () renvoie les probabilités d’une variable aléatoire distribuée logarithmiquement normale. Utilisez cette fonction pour évaluer les distributions de probabilités où le logarithme naturel au lieu de la variable aléatoire est distribué normalement.

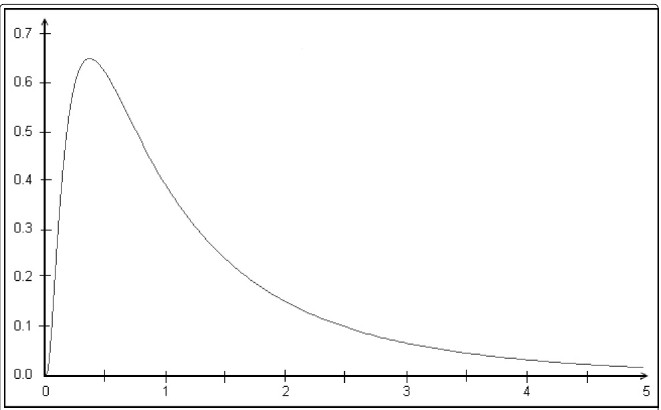
La distribution log-normale est similaire à la distribution normale mais a un logarithme dans l’exposant. La distribution log-normale est asymétrique à droite (voir la figure 12-91 plus loin dans cette section). Si une variable aléatoire est distribuée log-normale, son logarithme est également distribué normalement. Par exemple, les revenus sont souvent lognormaux. La raison en est le pourcentage d’augmentation habituel. Les revenus élevés augmentent beaucoup et les revenus plus modestes n’augmentent que très peu. Avec le temps, les petits revenus restent modestes et les gros revenus deviennent plus importants. Par conséquent, la distribution est juste asymétrique. La fonction logarithmique transforme la structure multiplicative en une structure additive. Les valeurs logarithmisées sont alors distribuées normalement.

Une autre raison de la structure de revenus distribuée log-normale est le manque d’emplois bien rémunérés. Le salaire pour la majorité des emplois est faible, mais les revenus extrêmement bas sont moins courants. La plupart des distributions log-normales sont basées sur ce fait.

La distribution log-normale avec les paramètres p et G2 pour les nombres réels positifs est définie par la densité de probabilité suivante:

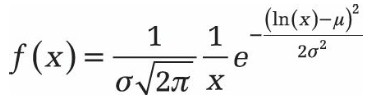
La figure montre la densité de probabilité de la distribution log-normale.

L’equation pour la fonction de distribution d’une distribution lognormal.

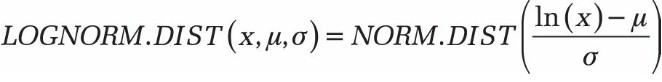
Exemple.

Utilisez les valeurs suivantes pour calculer LOI.LOGNORMALE.N ():

■ 4 = la valeur à laquelle évaluer la fonction (x)

■ 3,5 = la moyenne de ln (x) (moyenne)

■ 1,2 = cde ln (x) (ecart_type)

■ TRUE = la valeur logique qui représente le type de la fonction. La Figure illustre le calcul de LOI.LOGNORMALE.N ().

La figure montre le calcul de LOI.LOGNORMALE.N ().

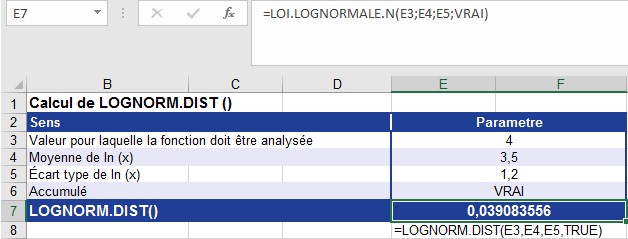
La fonction LOI.LOGNORMALE.N () renvoie la distribution lognormale cumulative de 0,039084 en fonction des paramètres illustrés à la figure.