Syntaxe.
LOI.NORMAL.INVERSE (probabilité; moyenne; standard_dev)
Définition.
Cette fonction renvoie le quantile de la distribution normale.
Arguments
probabilité (obligatoire). Une probabilité associée à la moyenne normale de distribution normale (requise). La moyenne arithmétique de la distribution standard_dev (obligatoire). L’écart type de la distribution
Contexte.
Une distribution normale normalisée est une distribution normale avec la valeur moyenne 0 et l’écart type 1. Chaque distribution normale peut être transformée en une distribution normale standard en soustrayant la moyenne des valeurs xi et en divisant la différence par l’écart type.
La distribution normale standard étant normalisée, vous pouvez calculer la plage de la distribution normale à partir des valeurs z à l’aide de la formule suivante:
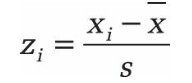
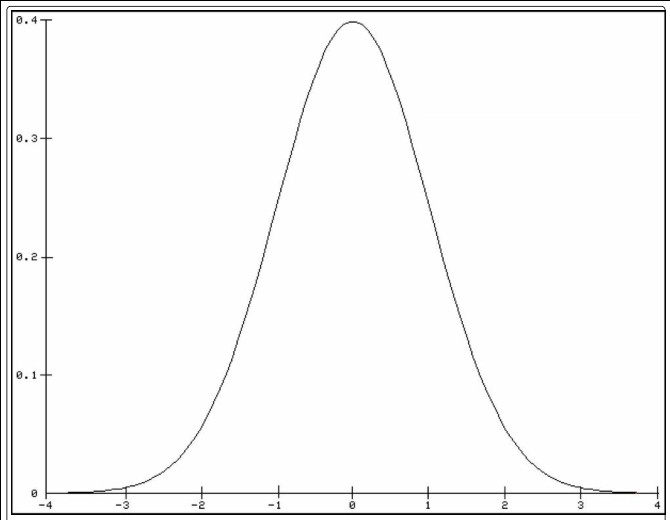
Pour la fonction de densité de la distribution normale standard, les intervalles sont 1, 2 et 3 écarts types par rapport à la valeur attendue 0 (voir la figure). Ces plages représentent environ 68%, 95,5% et 99,7% de la courbe en cloche. Les mêmes pourcentages s’appliquent à toutes les distributions normales en ce qui concerne les valeurs attendues et les écarts types.
Exemple.
Vous êtes un fabricant d’ampoules électriques et souhaitez analyser les performances des ampoules électriques. Vous avez également calculé le cycle de vie moyen et l’écart type associé. Maintenant vous voulez
connaître les performances de 85% et 15% de vos ampoules en fonction des valeurs moyennes et de l’écart type.
Pour ce calcul, vous utilisez la fonction LOI.NORMAL.INVERSE () avec les arguments suivants:
probabilité = 85% (15%); c’est-à-dire que vous calculez la performance de 85% (15%) des ampoules
moyenne = 2 000 heures (calculée à partir de la population n)
standard_dev = 579 heures (calculées à partir de la population)
La figure montre les résultats.
NORM.INV () renvoie les performances de 85% ou 15% des ampoules.
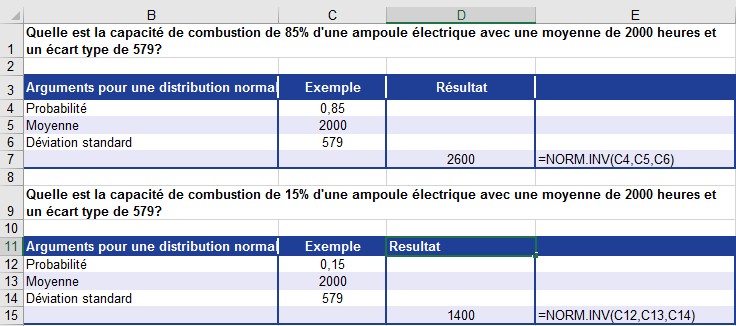
Vous pouvez faire les déclarations suivantes à partir de ces résultats:
85% des ampoules ont une performance allant jusqu’à 2 600 heures.
15% des ampoules ont une performance allant jusqu’à 1 400 heures
