Syntaxe.

LOI.NORMAL.N (x; moyenne; standard_dev; cumulative)

Définition.

Cette fonction renvoie la distribution normale pour une valeur moyenne et une variance standard. Cette fonction a un très large éventail d’applications en statistique, y compris le test d’hypothèses.

Arguments

x (requis). La valeur de distribution (quantile) pour laquelle vous voulez calculer la probabilité.

moyenne (obligatoire). La moyenne arithmétique de la distribution.

standard_dev (obligatoire). L’écart type de la distribution.

cumulatif (obligatoire). La valeur logique qui représente le type de la fonction. Si cumulative vaut VRAI, la fonction LOI.NORMAL.N () renvoie la valeur de la fonction de distribution (fonction de densité cumulative). Si cumulative vaut FAUX, la fonction LOI.NORMAL.N () renvoie la valeur de la fonction de densité.

Contexte.

Excel offre de nombreuses fonctions pour calculer les distributions et évaluer les hypothèses.

Un exemple est la fonction LOI.NORMAL.N (). En général, les distributions aident à répondre aux questions concernant les probabilités. Un exemple est un tirage au sort qui n’a que deux probabilités: têtes ou queues.

Comme déjà mentionné, la fonction LOI.NORMAL.N () renvoie la distribution normale de valeurs données.

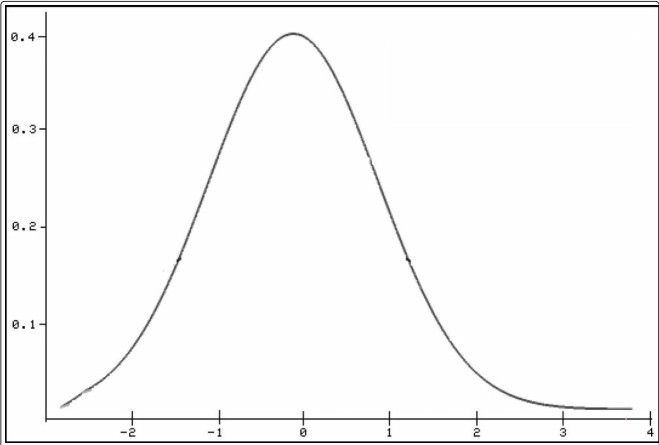
La distribution normale est la distribution de probabilité continue la plus importante qui indique la probabilité d’une valeur pour une variable aléatoire x. La densité de probabilité est aussi appelée la  gaussienne fonction, courbe gaussienne, cloche gaussienne ou courbe de cloche et est représentée à la figure.

Différentes fonctions de densité pour les variables aléatoires distribuées normales.

La signification particulière de la distribution normale est basée sur le théorème de la limite centrale qui stipule qu’une somme de n variables aléatoires distribuées identiques indépendantes est normale distribuée à la limite.

La distribution normale explique de nombreux processus scientifiques exactement ou approximativement, en particulier ceux qui fonctionnent indépendamment les uns des autres dans des directions différentes.

Contrairement à la distribution binomiale, la distribution normale est symétrique (comme le montre la figure).

Cela signifie que la distribution normale est similaire à une courbe en cloche où la valeur la plus petite et la plus grande ont la probabilité la plus faible et la valeur moyenne, la probabilité la plus élevée.

Notez ce qui suit pour une distribution normale:

C’est en forme de cloche.

C’est unimodal.

Il est asymptotiquement proche de l’axe des x.

C’est symétrique.

Les déclarations suivantes sont également vraies:

Le maximum est à la moyenne arithmétique.

Chaque tranche de 50% de la plage est bilatérale par rapport à la moyenne arithmétique.

La moyenne arithmétique et la médiane sont congruentes.

Le mode, la médiane et la moyenne arithmétique sont congruents.

Les points d’inflexion sont à la valeur moyenne plus l’écart type et à la valeur moyenne moins l’écart type.

Excel offre deux fonctions pour la plupart des distributions. Une fonction qui calcule une distribution et se termine par DIST calcule la probabilité pour une certaine valeur. La fonction inverse associée, se terminant par INV, calcule la valeur pour une certaine probabilité.

L’équation pour la fonction de densité de la distribution normale (cumulative = FALSE) est la suivante:

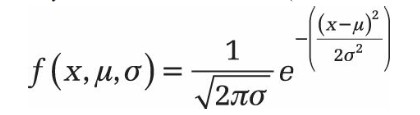
Exemple.

Vous êtes un fabricant d’ampoules électriques et souhaitez analyser les performances des ampoules électriques. Toi ont également calculé le cycle de vie moyen et l’écart type associé. Tu veux savoir la probabilité que les ampoules durent plus longtemps ou moins longtemps lorsqu’elles sont utilisées quotidiennement. Pour ce calcul, vous utilisez la fonction LOI.NORMAL.STANDARD.N (). Le cycle de vie de vos ampoules est normal avec:

2 000 heures de travail en moyenne = moyenne heure moyenne

Un écart type de 579 heures = argument type ecart

Pour calculer la fonction de distribution, vous spécifiez la valeur logique VRAI pour la valeur cumulative.

argument. Si vous souhaitez calculer la fonction de densité, utilisez la valeur logique FAUX.

Vous posez la question suivante: Quelle est la probabilité qu’une ampoule fonctionne jusqu’à 2600 heures?

ou seulement jusqu’à 1400 heures? Et quelle est la probabilité que ces heures soient exactement atteintes?

Les valeurs 2 600 heures et 1 400 heures sont indiquées par l’argument x. Ce sont les valeurs de la distribution pour lesquelles vous voulez calculer la probabilité. La figure  montre les résultats.

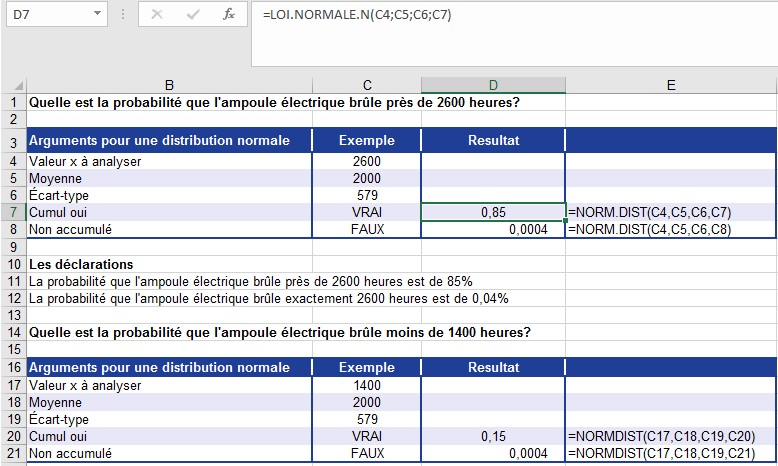
 Calcul de la probabilité pour différentes performances.

Quelles conclusions pouvez-vous tirer de ces résultats?

La probabilité qu’une ampoule fonctionne pendant 2 600 heures est de 85%.

La probabilité qu’une ampoule fonctionne exactement 2 600 heures est de 0,04%.

De cette manière, vous pouvez effectuer de nombreux calculs, tester des hypothèses et spécifier les probabilités des caractéristiques par intervalles.