Syntaxe.

LOI.POISSON.N (x; moyenne; cumulative)

Définition.

Cette fonction renvoie les probabilités d’une variable aléatoire distribuée de Poisson. Une application courante de la distribution de Poisson est la prédiction du nombre d’événements sur une période donnée, telle que le nombre d’appels reçus par un centre d’appels au cours d’une heure.

Arguments

■ x (obligatoire). Le nombre d’événements.

■ moyen (obligatoire). La valeur numérique attendue.

■ cumulatif (obligatoire). La valeur logique qui représente le type de la fonction. Si cumulative vaut TRUE, LOI.POISSON.N () renvoie la probabilité de Poisson cumulative que le nombre d’événements aléatoires se produisant se situe entre zéro et x inclusivement. Si cumulative vaut FALSE, la fonction renvoie la probabilité que le nombre d’événements survenus soit exactement x.

Contexte.

La fonction LOI.POISSON.N () (nommée d’après Denis Poisson, 1781-1840) renvoie les probabilités d’une variable aléatoire distribuée de Poisson. La distribution de Poisson prédit la fréquence d’événements similaires indépendants à partir d’un grand nombre d’éléments.

Un exemple est le nombre de clients arrivant sur un centre commercial ou le nombre d’appels téléphoniques entrants.

La distribution de Poisson est particulièrement utile pour les distributions de probabilité comportant de nombreux résultats provenant d’un échantillon et une faible probabilité que l’événement se produise. Dans ce cas, la distribution de Poisson est similaire à la distribution binomiale. Contrairement à la distribution binomiale, la distribution de Poisson (en plus de x) nécessite un seul paramètre: la valeur attendue ou l’argument moyen.

Pour les faibles probabilités, la distribution binomiale se rapproche de la distribution de Poisson. Cela signifie que la distribution s’applique si le nombre moyen d’événements est le résultat d’un grand nombre de possibilités d’événements et d’un faible nombre de probabilités d’événements. La désintégration radioactive est souvent utilisée à titre d’exemple. Dans un très grand nombre d’atomes, seule une très petite quantité d’atomes se désintègre dans un intervalle de temps. La désintégration est aléatoire et indépendante des atomes déjà décomposés. C’est une exigence importante pour la distribution de Poisson.

La distribution de Poisson suppose que l’événement se produit rarement dans un certain intervalle de temps. Cependant, la distribution dépend uniquement de la longueur de l’intervalle et est indépendante de la position sur l’axe des temps. Par conséquent, vous pouvez utiliser la distribution de Poisson pour calculer la probabilité d’erreur ou un événement par intervalle.

La fonction LOI.POISSON.N () calcule les formules suivantes:

■ Pour cumulatif = FAUX:

Pour cumulatif = VRAI:

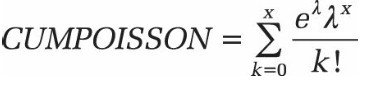
Pour ces formules, la fonction POISSON.DIST () remplace x par le nombre d’événements et mean par le nombre attendu. L’argument cumulatif indique si la moyenne est atteinte exactement (cumulatif = FAUX) ou au maximum (cumulatif = VRAI).

Exemple.

Vous êtes un revendeur de pneus et vendez votre propre marque. Vous avez analysé la qualité de votre marque sur une longue période. Il s’est avéré qu’avec vos pneus, il se produisait en moyenne quatre incidents de dommages par 100 000 milles (voir la figure).

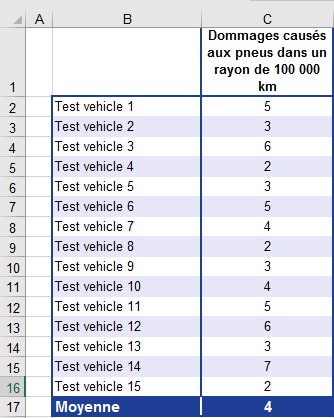
Figure L’analyse des pneus indique un taux d’erreur de quatre. par 100 000 milles.

Comparés à l’intervalle de 100 000 km, ces quatre événements sont rares. Par conséquent, vous utilisez la distribution de Poisson. Vous posez la question suivante: Quelle est la probabilité que trois incidents d’endommagement des pneus par 100 000 milles ne se produisent?

Vous entrez les valeurs suivantes pour les arguments requis par la fonction POISSON.DIST ():

■ x = 3 (nombre d’événements que vous souhaitez évaluer)

■ moyenne = 4 (nombre d’événements attendus)

■ cumulative = FALSE (parce que vous voulez calculer la probabilité que x événements se produisent)

La figure montre le résultat.

Figure Calculer la probabilité pour exactement trois événements.

La fonction POISSON () renvoie une probabilité de 19,54% que trois incidents de dégât de pneu par 100 000 km se produisent. Pour calculer la probabilité de 0 à x incidents de dégât de pneu par 100 000 km, indiquez la valeur logique VRAI pour l’argument cumulatif (voir la figure).

Figure Calcul de la probabilité de 0 à 3 événements.

La fonction LOI.POISSON.N () () renvoie une probabilité de 43,35% pour que 0 à 3 incidents de dégâts de pneus par 100 000 km se produisent.