MOYENNE (nombre1; nombre2; …)

Définition.

Cette fonction renvoie la moyenne (moyenne arithmétique) des arguments. Pour calculer la moyenne, les variables à échelle d’intervalle sont ajoutées puis divisées par leur nombre.

Arguments

■ nombre1 (requis) et nombre2 (facultatif). Au moins un et jusqu’à 255 arguments (30 dans Excel 2003 et versions antérieures) pour lesquels vous souhaitez calculer la moyenne

Contexte.

La moyenne arithmétique est la valeur moyenne la plus connue et est largement acceptée par les non-statisticiens. Comme la valeur moyenne peut facilement être calculée en fonction de toutes les valeurs, elle joue un rôle important dans les statistiques inférentielles.

Pour calculer la valeur moyenne, les valeurs d’une plage sont ajoutées et la somme est divisée par le nombre de valeurs. Le calcul de la moyenne arithmétique nécessite l’échelle d’intervalle. La formule pour calculer la moyenne arithmétique est la suivante:

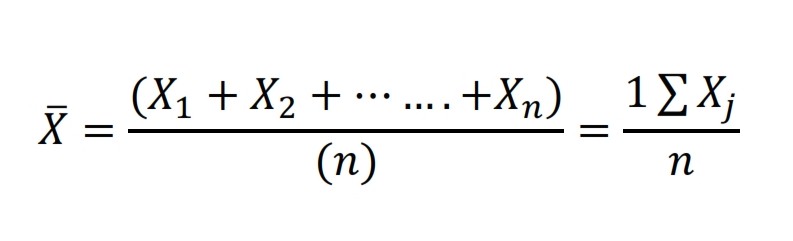
La moyenne commune peut être calculée à partir de la moyenne arithmétique de deux ensembles de données.

Le principal inconvénient de la moyenne arithmétique est que les valeurs extrêmes sont importantes car toutes les valeurs sont incluses. En outre, la tendance centrale pourrait être à un endroit avec seulement quelques valeurs observées, voire aucune.

Pour les valeurs groupées, la moyenne arithmétique n’est qu’une estimation et ne peut pas être calculée pour des variables continues lorsqu’il n’existe aucune information supplémentaire concernant l’estimation de la tendance centrale.

Bien que le calcul de la moyenne arithmétique nécessite une échelle métrique, les valeurs moyennes des données à l’échelle ordinale peuvent également être calculées. Cela inclut des ensembles de données telles que celles qui consistent en des réponses aux questions concernant la satisfaction de la clientèle pour certains services. Cela est autorisé car une distribution normale des données peut être supposée si les échantillons sont suffisants et un intervalle de confiance est indiqué par la valeur moyenne réelle d’une distribution. La valeur moyenne et la variance d’un échantillon suffisant (n> 30) sont requises.

Pour les données qui permettent de calculer la moyenne arithmétique, le mode et la médiane peuvent également être calculés. La meilleure des trois mesures de la tendance centrale à utiliser dépend de la question. La valeur moyenne, le mode et la médiane utilisent des informations différentes et ont généralement des valeurs numériques différentes. Bien que la moyenne arithmétique soit la mesure la plus commune de la tendance centrale, il peut être nécessaire d’utiliser le mode ou la médiane en raison de la faible échelle ou des valeurs aberrantes.

Exemple.

Vous êtes le responsable marketing de la société de logiciels et devez calculer le nombre moyen de visites par page Web en 2007. Sur la base de cette évaluation, la société est en mesure de déterminer les zones les plus visitées et d’améliorer celles qui comptent moins de visiteurs.

Supposons que vous avez importé les données de votre système dans un fichier Excel. Avec un tableau croisé dynamique, vous pouvez facilement calculer et analyser les visites des zones individuelles. Vous êtes intéressé par les domaines Produits, Publications, Équipe, Formation et Connaissances, ainsi que par le résultat général. Vous calculez la moyenne des visites pour chaque zone en utilisant la fonction MOYENNE() pour voir la popularité de chaque zone. Comme vous pouvez le voir à la figure ,la zone Produits a beaucoup plus de visites que la zone Publications.

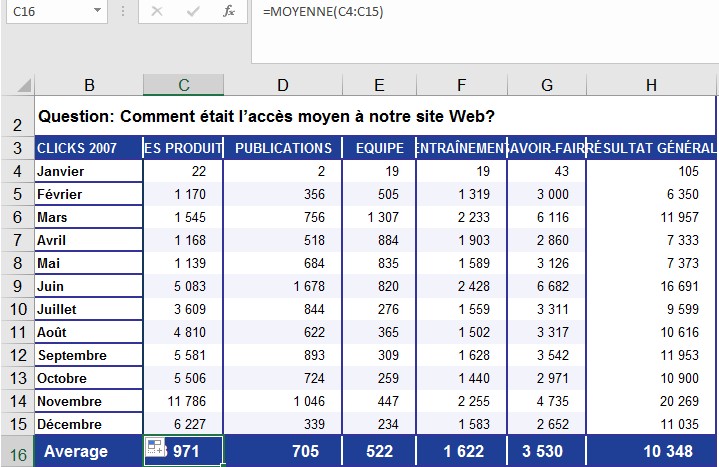
Vous pouvez également calculer la moyenne des visites sur le site Web pour toutes les régions au cours d’une année afin d’obtenir un aperçu de l’ensemble de l’activité du site Web. Si vous disposez des valeurs comparatives de l’année précédente, vous pouvez analyser davantage les données.