Syntaxe.
PEARSON (tableau1; tableau2)
Définition.
Cette fonction renvoie le coefficient de corrélation de Pearson r. Ce coefficient est un indice sans dimension compris entre –1,0 et 1,0 inclus et reflète l’étendue d’une relation linéaire entre deux ensembles de données.
Arguments
tableau1 (requis). Un ensemble de valeurs indépendantes
tableau2 (requis). Un ensemble de valeurs dépendantes
Contexte.
Le coefficient de corrélation fournit une mesure quantitative de l’ampleur de la corrélation entre les caractéristiques métriques.
Dans Excel, le coefficient de corrélation est calculé avec la fonction PEARSON (). Vous pouvez entrer les deux ensembles de données dans les arguments tableau1 et tableau2. Le premier ensemble de données représente les valeurs de la variable indépendante x et le deuxième ensemble de données représente les valeurs de la variable dépendante y.
Le résultat renvoyé par PEARSON () pour r est compris entre -1 et +1. Mais que signifient les résultats?
r = -1 indique une corrélation négative – les ensembles de données sont indépendants les uns des autres.
r = +1 indique une corrélation positive – les ensembles de données dépendent les uns des autres.
Une valeur proche de r = 0 indique qu’il n’y a pas de corrélation linéaire.
La corrélation entre les deux caractéristiques doit être linéaire car la fonction PEARSON () ne calcule pas les corrélations non linéaires. Pour cette raison, la variance doit être prise en compte lors du calcul du coefficient de corrélation r. Sinon, le résultat pourrait indiquer qu’il n’y a pas de corrélation pour r même s’il existe une corrélation non linéaire (par exemple, exponentielle).
La valeur d’un coefficient de corrélation calculée par PEARSON () ou COEFFICIENT.CORRELATION () n’indique pas le sens de la corrélation entre deux variables. Pour une corrélation statistique, vous pourriez aussi avoir déterminé si la corrélation est irréelle ou réelle. Des corrélations irréelles se produisent souvent dans les séries chronologiques si les deux variables ont la même tendance. En général, une corrélation élevée ne doit être considérée que comme une indication de l’existence possible d’une corrélation.
L’équation du coefficient de corrélation de Pearson r est la suivante:
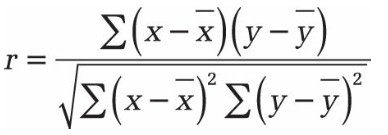
Les valeurs x et y sont les moyennes de l’échantillon MOYENNE (tableau1) et MOYENNE (tableau2).
Exemple.
Un éditeur de logiciels vend tous ses produits sur son site Web. La société envoie régulièrement des lettres d’information pour informer les clients existants et potentiels des nouveaux produits mis à jour et pour attirer l’attention sur son site Web. L’année dernière, les commandes sur le site Web ont considérablement augmenté. La direction veut savoir la raison. L’augmentation des ventes est-elle attribuable au marketing ou à la publicité? L’augmentation du nombre de visites sur le site Web a-t-elle entraîné une augmentation des ventes?
Cela signifie que l’entreprise souhaite connaître la corrélation entre les visites sur le site Web et les commandes en ligne. Un diagramme de dispersion et une ligne de tendance linéaire montrent déjà une corrélation linéaire entre le
variables x (visites de sites Web) et y (commandes en ligne) (voir la figure).
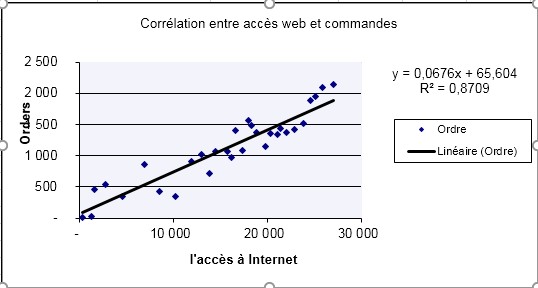
. Le diagramme de dispersion montre déjà une dépendance linéaire entre les variables.
REMARQUE
Si le diagramme de dispersion ne montre pas de corrélation linéaire entre les deux variables, vous devez utiliser la fonction CORREL () à la place de la fonction PEARSON ().
Le calcul du coefficient de corrélation r avec la fonction PEARSON () prouve qu’il existe une dépendance linéaire (voir la figure ).
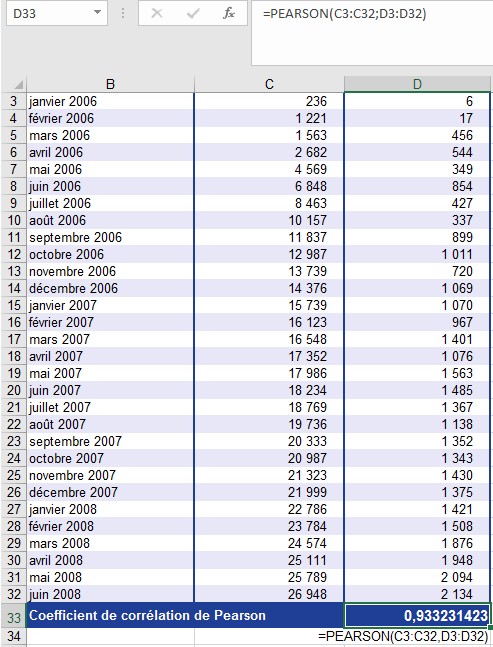
Le coefficient de corrélation de 0,933 indique une corrélation positive presque parfaite. Cela signifie que les visites sur le site Web et les commandes en ligne sont interdépendantes linéaires. Cela était déjà supposé sur la base du diagramme de dispersion (illustré précédemment dans la Figure ).
En d’autres termes, le coefficient de corrélation de 0,933 indique que le nombre de commandes en ligne augmente en même temps que le nombre de visites sur le site Web.
