Syntaxe.
PERMUT (nombre; nombre_choisi)
Définition.
Cette fonction renvoie le nombre de permutations permettant d’interroger k éléments à partir de n éléments. Une permutation est un ensemble d’éléments ou d’événements où l’ordre interne est significatif.
Arguments
■ nombre (obligatoire). Le nombre d’éléments
■ nombre_choisi (requis). Spécifie le nombre d’éléments pour une permutation
Contexte.
La fonction PERMUT () appartient à la combinatoire qui détermine le nombre de commandes possibles pour les objets. La fonction PERMUT () est différente de la fonction COMBIN (), pour laquelle l’ordre interne n’est pas significatif. Cela signifie que pour PERMUT (), l’ordre des éléments ne peut pas être modifié par la suite. Pour COMBIN (), cela n’a pas d’importance. Par exemple, la fonction PERMUT () calcule les probabilités pour les trois premières places dans une course à dix participants, alors qu’avec la fonction COMBIN (), vous pouvez calculer des probabilités de type loterie. La différence: bien que l’ordre des numéros de loterie puisse être modifié, les coureurs protesteraient si vous triiez les places du premier au troisième par la première lettre du nom de famille.
La fonction PERMUT () calcule le nombre d’échantillons ordonnés de k éléments à partir de n éléments. L’équation pour calculer le nombre de permutations est la suivante:
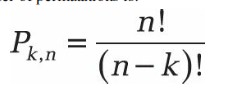
Exemple.
Prenons l’exemple de la course. Dix coureurs participent à la course. Les trois premiers coureurs reçoivent un prix et les autres coureurs ne reçoivent rien. Vous voulez connaître le nombre de variations possibles pour les trois premières places. Par conséquent, vous utilisez la fonction PERMUT ().
Quelles sont les valeurs spécifiées pour les arguments n et k?
■ n = 10 (le nombre d’éléments est égal au nombre de coureurs)
■ k = 3 (la permutation est composée de trois éléments, les trois premières places)
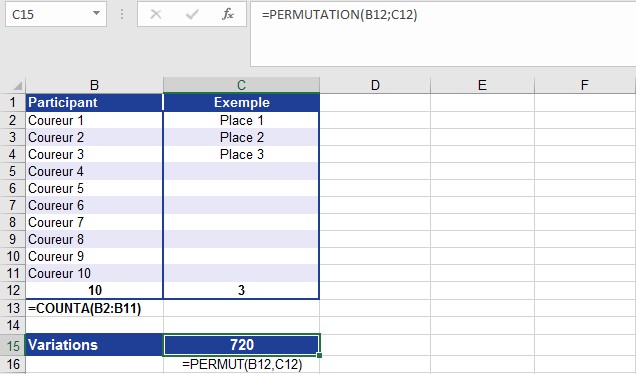
La fonction PERMUT () renvoie 720 possibilités différentes pour les gagnants des trois places.
