Syntaxe

T. TEST (matrice1; matrice2; queues; type)

Définition.

Cette fonction renvoie les statistiques de test du test t de Student. Utilisez T.TEST () pour vérifier si deux échantillons sont susceptibles d’être issus des mêmes deux populations ayant la même moyenne.

Arguments

■ matrice1 (obligatoire). Le premier ensemble de données.

■ matrice2(requis). Le deuxième ensemble de données.

■ queues (obligatoire). Spécifie le nombre de queues de distribution. Si queues = 1, la fonction T.TEST () utilise

la distribution unilatérale. Si queues = 2, la fonction T.TEST () utilise la distribution à deux queues.

■ type (obligatoire). Le type de test t à effectuer :

– Si le type est égal à 1, le test est jumelé.

– Si le type est égal à 2, le test de variance égale (homoscédastique) est effectué.

– Si le type est égal à 3, le test de variance inégale à deux échantillons (hétéroskédastique) est effectué.

Contexte.

Les fonctions de distribution t indiquent si un ou deux échantillons correspondent à la distribution normale. Par exemple, vous pouvez tester si une méthode de traitement est meilleure qu’une autre.

La distribution t appartient aux distributions de probabilité et a été développée en 1908 par William Sealey Gosset (alias «Student»). William Gosset a découvert que les données distribuées normales normalisées ne le sont plus si la variance de la caractéristique est inconnue et que la variance de l’échantillon doit être utilisée pour une estimation.

La distribution t est indépendante de la moyenne g et de l’écart type s et ne dépend que des degrés de liberté.

Étant donné que la distribution normale ne s’applique qu’à une grande quantité de données, elle doit généralement être corrigée. Cette incertitude est observée dans une distribution t par la distribution symétrique. S’il y a beaucoup

Plus les degrés de liberté sont faibles, plus les limites intégrales de la moyenne sont éloignées de la moyenne sur la base d’une probabilité donnée et d’un écart-type fixe tels que, pour un test bilatéral, l’intervalle soit supérieur à 1,96 (pour P = 0,95).

La distribution t décrit la distribution d’un terme:

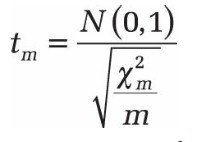
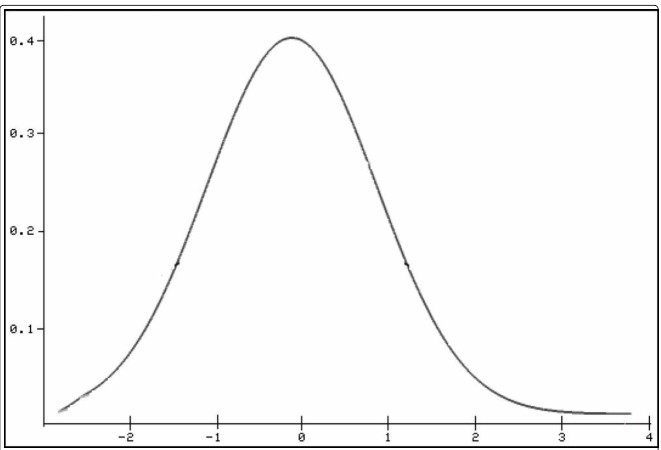
N (0.1) est une variable aléatoire standard normale distribuée et une variable% 2 distribuée avec m degrés de liberté. La variable de compteur doit être indépendante de la variable dénominateur. La fonction de densité de la distribution t est symétrique en fonction de la valeur attendue 0 (voir la figure).

Le test t permet des hypothèses pour des échantillons plus petits si la population présente une distribution normale, une certaine moyenne est supposée et que l’écart type est inconnu.

Il existe trois types de tests t:

■ Comparaison des moyennes de l’échantillon avec les moyennes de la population. Un exemple est la comparaison de l’âge moyen de la population new-yorkaise avec celui de l’ensemble de la population des États-Unis.

■ Comparaison moyenne d’échantillons indépendants Un exemple est la comparaison du revenu moyen des hommes et des femmes à New York. Comme les variances des deux populations à partir desquelles les échantillons ont été obtenus sont inconnues, les variances de l’échantillon sont estimées. La distribution t est suivie d’un test t avec k degrés de liberté

■ Comparaison des moyennes d’échantillon à partir d’échantillons interdépendants. Un exemple est la comparaison de l’éducation des conjoints. Une caractéristique d’un échantillon est évaluée deux fois et testée si la deuxième valeur est supérieure (ou inférieure) à la première valeur. La distribution t est suivie par une valeur t avec n -1 degrés de liberté. N est le nombre de paires de valeur.

La question à laquelle le test t répond est la suivante: quelle est la probabilité que la différence entre les moyennes soit aléatoire? Et quelle est la probabilité d’erreur alpha si, en vous basant sur les différentes moyennes de l’échantillon, vous supposez que cette différence existe aussi dans la population?

En d’autres termes, le test t évalue la probabilité (d’erreur) d’une thèse sur la base d’échantillons, c’est-à-dire qu’il évalue la probabilité d’une erreur alpha.

Types de tests t. Il existe deux distinctions générales entre les différents types de test t:

■ Test t unilatéral Pour un test t unilatéral, des hypothèses directionnelles sont préparées. Où Ho et H1:

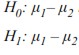               H_0:  inférieur ou égal à 0

                                      H_1: supérieur à 0

Pour atteindre un niveau alpha classique (niveau de signification) de 5%, t doit être positionné du côté prévu de la distribution t dans la plage de 5% (voir la figure).

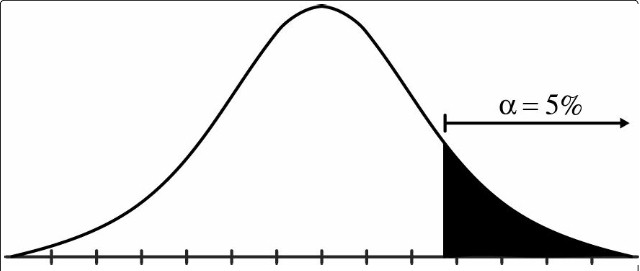
Figure . Graphique d’un test t unilatéral.

■ Test t bilatéral. Pour un test t bilatéral, des hypothèses non directionnelles sont préparées. Où H₀ et H₁:

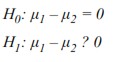
Pour atteindre un niveau alpha global (niveau de signification) de 5%, t doit être placé dans la plage inférieure ou supérieure à 2,5% (voir la figure ).

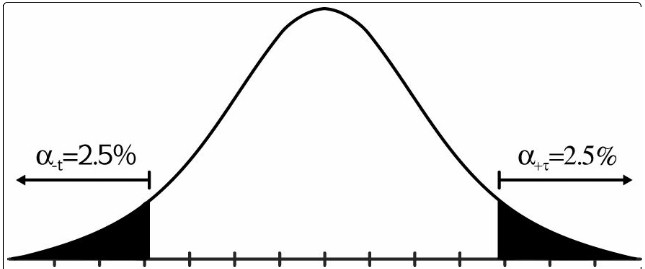
■ Pour un test bilatéral, t doit avoir une valeur plus élevée pour être significatif 

■ Pour un test bilatéral, t est associé à une probabilité d’erreur plus élevée que pour un test unilatéral.

■ Un test unilatéral offre des performances de test supérieures.

■ x₁-x₂ est plus susceptible d’être significatif dans un test unilatéral que dans un test bilatéral

■ Un test unilatéral offre des performances de test supérieures.
Pour un test bilatéral, la valeur t se voit généralement attribuer le double de la valeur p attribuée au test unilatéral. Cette valeur p peut être convertie en valeur p pour un test unilatéral (et inversement).

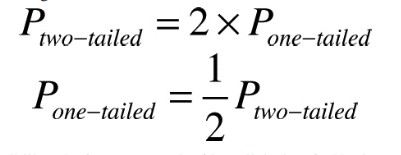
Exemple.

La compatibilité d’un médicament a été examinée dans le cadre d’une étude clinique. Vous avez les résultats du test ainsi que des explications. Un groupe de test a pris la posologie quotidienne normale et l’autre groupe de test a pris une posologie augmentée au début de l’étude. Une personne a dû annuler le test tôt pour des raisons privées. L’objectif était de déterminer si l’augmentation de la dose accélère le processus de guérison.
La durée du traitement a été calculée en jours.
L’hypothèse nulle indique qu’il n’y a pas de différence entre les deux groupes de test en ce qui concerne le succès du traitement. L’hypothèse alternative indique que le deuxième groupe s’est rétabli plus rapidement car la méthode de traitement est plus efficace que le traitement habituel. Vous devez analyser les résultats du test pour déterminer si l’hypothèse nulle peut être acceptée ou doit être rejetée.
Étant donné que vous n’étiez pas présent pendant le test et que vous ne disposez pas de toutes les informations de base, vous souhaitez calculer la probabilité que les moyennes des deux échantillons soient égales à l’aide de la fonction T.TEST (). En comparant le résultat au niveau de signification, vous pouvez tirer une conclusion sur l’hypothèse nulle.

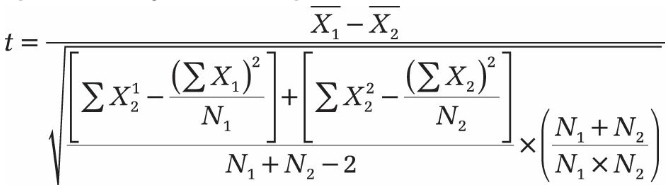
Les valeurs x sont les moyennes du groupe 1 et du groupe 2; N₁ et N₂ indiquent la taille des deux échantillons. La figure  montre le résultat de l’étude.

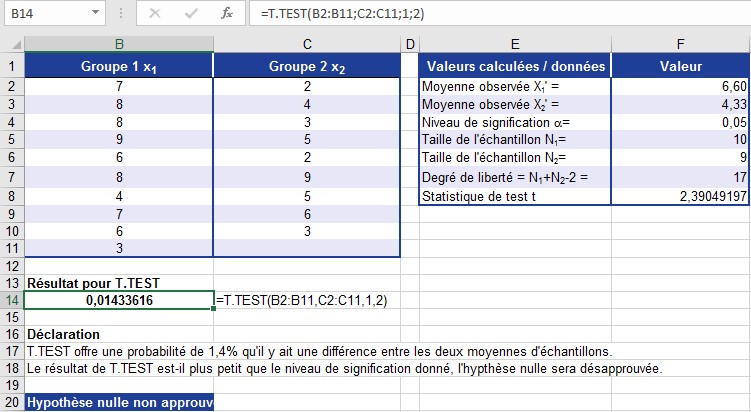
Figure Les moyennes des deux échantillons sont-elles égales? T.TEST () est utilisé pour calculer le résultat.

Comme T.TEST () renvoie une valeur de probabilité, le résultat est 1,4%. Vous pouvez maintenant supposer, avec une probabilité de 1,4%, que les moyennes de l’échantillon ne sont pas égales. En d’autres termes: vous pouvez dire avec 1,4% de certitude que les échantillons sont inégaux. Ceci est déjà montré dans les cellules F2 et F3 de la figure. Cependant, ce ne sont que des valeurs estimées basées sur des échantillons.

Comme le résultat de T.TEST () est <a, l’hypothèse nulle doit être rejetée. Cela signifie que la déclaration selon laquelle il n’y a pas de différence entre les deux groupes de test en ce qui concerne le succès du traitement est ignorée.