Syntaxe.
TENDANCE (y_connus; x_connus; nouveau_x; const)
Définition. Cette fonction renvoie les valeurs le long d’une tendance linéaire. TENDANCE () adapte une ligne droite (à l’aide de la méthode des moindres carrés) aux tableaux y_connus et x_connus. La fonction renvoie les valeurs y le long de cette ligne pour le tableau spécifié de nouveau_x.
Arguments
■ y_connus (requis). Les valeurs y que vous connaissez déjà de la relation y = mx + b:
– Si le tableau y_connus consiste en une seule colonne, chaque colonne du tableau x_connus est interprétée comme une variable distincte.
– Si le tableau y_connus consiste en une seule ligne, chaque ligne du tableau x S connu est interprétée comme une variable distincte.
■ x_connus (facultatif). Les valeurs x que vous connaissez déjà de la relation y = mx + b:
– Le tableau x S connu peut inclure un ou plusieurs ensembles de variables. Si une seule variable est utilisé, pas_y et x S connus peuvent être des plages de n’importe quelle forme, à condition que leurs dimensions soient égales. Si plusieurs variables sont utilisées, y_connus doit être un vecteur (une plage composée d’une seule ligne ou d’une seule colonne).
– Si x x n’est pas spécifié, il est supposé être le tableau {1,2,3, …} contenant le même nombre d’éléments que le paramètre y_connus.
– Les arguments y_connus et x S connus doivent avoir le même nombre de lignes ou de colonnes. Si le nombre de lignes (colonnes) est différent, vous obtenez le # REF! Erreur. Si l’une des valeurs y est 0 ou négative, vous obtenez le #NOM! Erreur.
■ nouveau_x (facultatif). Les nouvelles valeurs x pour lesquelles vous souhaitez renvoyer les valeurs y correspondantes:
– Tout comme x x connu, l’argument nouveau_x doit inclure une colonne (ou une ligne) pour chaque variable indépendante. Les arguments x S et new x S connus doivent avoir le même nombre de colonnes si pas_y est dans une seule colonne. Si y_connus est sur une seule ligne, x S et new x S connus doivent avoir le même nombre de lignes.
– Si new x S n’est pas spécifié, il est supposé être le même que connu x S.
– Si les deux x S connus et les nouveaux x S sont omis, ils sont supposés être le tableau {1, 2, 3, …} qui contient le même nombre d’éléments que le paramètre pas_y .
■ const (facultatif). Une valeur logique spécifiant s’il faut forcer la constante b à être égale à 1:
– Si conSt est VRAI ou omis, b est calculé normalement.
– Si conSt est FALSE, b est égal à 1 et les valeurs m sont ajustées pour que y = mAx.
Contexte.
Si vous savez que différentes valeurs sont interdépendantes, vous pouvez effectuer une prédiction basée sur les valeurs connues.
Excel fournit de nombreuses fonctions statistiques que vous pouvez utiliser pour calculer des tendances. Les fonctions statistiques calculent une ligne ou une courbe en fonction de valeurs connues. Si vous étendez l’axe des temps, vous pouvez afficher les valeurs futures. Les valeurs connues sont analysées et décrites avec une formule permettant d’extrapoler les valeurs. Cependant, le jeu de données doit être suffisant pour compenser les variations saisonnières. D’autres facteurs imprévisibles ayant une incidence sur la tendance peuvent également poser problème.
Par exemple, considérons le cas dans lequel un concurrent réalise des ventes énormes avec un nouveau produit dans votre région. Comme l’analyse de régression suppose que les données peuvent être approximées à l’aide d’une fonction mathématique, Excel fournit bon nombre de ces fonctions, y compris TENDANCE ().
Utilisez la fonction TREND () pour calculer une tendance linéaire ou pour analyser des valeurs connues. Les valeurs sont entrées dans une formule et vous permettent de prévoir les tendances futures.
Les valeurs y et les valeurs x sont les valeurs de y = mx + b, où l’interception b indique l’interception de la ligne avec l’axe des y et la pente m indique l’ampleur de la modification de la valeur y en cas de modification de la valeur x.
Si les valeurs changent toujours d’une certaine valeur, une tendance linéaire existe.
Exemple.
Vous êtes le responsable marketing d’une société de logiciels et analysez le site Web de la société. Récemment, les visites sur le site Web ainsi que les commandes en ligne ont considérablement augmenté. Comme vous souhaitez connaître la tendance future des deux composants, vous utilisez la fonction TENDANCE () pour calculer les valeurs futures permettant de prévoir le nombre estimé de visites de sites Web et de commandes en ligne.
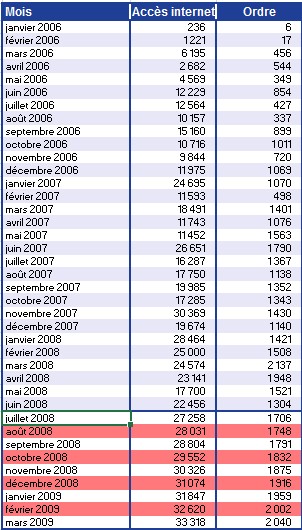
Les visites sur le site Web et les commandes jusqu’en juin 2008 sont illustrées à la figure.
Vous créez un graphique à partir des valeurs générées jusqu’à présent pour afficher la tendance linéaire des visites sur le site Web et des commandes en ligne, y compris les équations et la valeur calculée pour r2 (voir la figure).
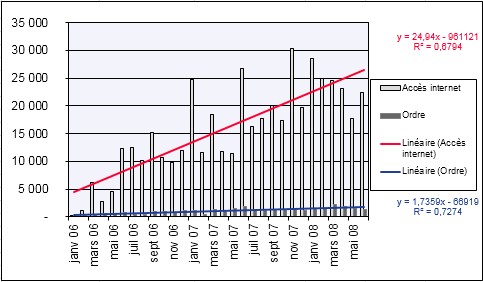
Figure Tableau des visites sur le site et des commandes en ligne.
La ligne de tendance linéaire et la fonction associée indiquent que les ordres augmentent de 52,872 par mois. Cela signifie environ 53 nouvelles commandes par mois. Vous souhaitez maintenant connaître la tendance des visites sur le site Web et des commandes en ligne de juillet 2008 à mars 2009.
La fonction TENDANCE () fournit les arguments suivants pour calculer les visites sur le site Web au cours des neuf prochains mois:
■ y_connus = visites du site Web entre janvier 2008 et juin 2008
■ x_connus = mois (janvier 2006 à juin 2008)
■ mois de nouveau_x = de juillet 2008 à mars 2009
■ const = TRUE (la constante b de l’équation
■ y = mx + b est calculé normalement)
La figure montre le résultat.
REMARQUE
N’oubliez pas que la fonction TREND () est une fonction de tableau lorsqu’elle calcule les valeurs pour la plage de cellules C33C41. Cela signifie que la fonction renvoie immédiatement le résultat pour tous les mois. Par conséquent, vous avez la plage de cellules sélectionnée C33: C41, entrez la formule et appuyez sur Ctrl + Maj + Entrée.
Vous pouvez reconnaître les fonctions de tableau à l’aide des accolades dans la barre de formule (voir la figure).
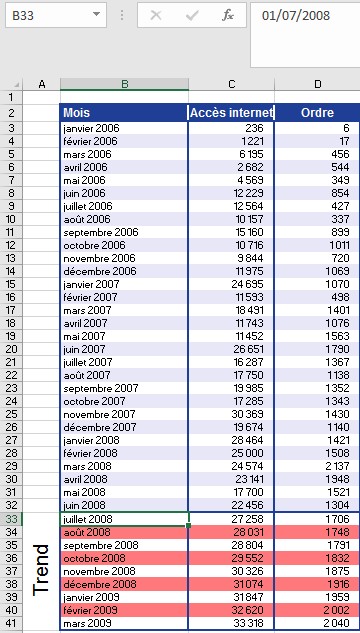
En utilisant la même procédure, vous pouvez calculer les valeurs des commandes en ligne en fonction des valeurs de tendance calculées pour les visites de sites Web. La figure 12-148 illustre le résultat et les arguments de la fonction TREND (). Avec la fonction TREND (), Excel permet un bon pronostic des visites sur le site Web et des commandes en ligne, en supposant que la tendance exponentielle précédente se poursuive.
