Syntaxe.

VAR. S (numéro1, numéro2, …)

Définition.

Cette fonction estime la variance à partir d’un échantillon. VAR.S () indique comment les données sont réparties autour de la moyenne.

Arguments

■ nombre1 (requis) et nombre2 (facultatif). Au moins un et jusqu’à 255 arguments (30 dans Excel 2003 et versions antérieures) correspondant à un échantillon de la population

Contexte.

Les écarts les plus couramment utilisés dans les statistiques sont la variance et l’écart type. La variance indique l’écart d’une variable aléatoire x par rapport à la valeur attendue E (x). En d’autres termes, la variance est la moyenne de l’écart au carré d’une valeur unique divisée par le nombre de valeurs. Le résultat est également appelé variance empirique.

Les écarts suivants existent:

■ Variance d’une variable aléatoire. L’écart au carré moyen des caractéristiques de la population. La fonction à utiliser est VAR.P ().

■ Variance de l’échantillon. Variance des valeurs observées à partir d’un échantillon d’une population. Cette variance est utilisée dans les statistiques descriptives pour mesurer la dispersion des données. Dans les statistiques inférentielles, cette variance estime la variance inconnue dans une population. La fonction à utiliser est VAR.S ().

Si la donnée évaluée est un échantillon, la somme des écarts carrés n’est pas divisée par le nombre de valeurs (n) mais par le nombre moins un (n – 1). VAR.S () utilise la formule suivante:

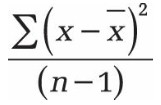
La valeur x est la moyenne de l’échantillon MOYENNE (nombre1, nombre2, …) et n est le jeu de données de l’échantillon. Notez qu’en raison de la quadrature, la valeur extrême pourrait avoir un poids plus élevé.

L’inconvénient de la variance est qu’il utilise une unité autre que les données (unités au carré). Par conséquent, l’écart type défini comme racine carrée de la variance est souvent utilisé.

Exemple.

Étant donné que la variance de l’échantillon mesure la dispersion des données, elle est souvent utilisée dans les statistiques descriptives. Le service marketing de l’éditeur de logiciels utilise la fonction VAR.S () pour créer une évaluation détaillée des visites du site. L’objectif est d’obtenir des informations plus précises et d’améliorer les domaines individuels.

Notez que les données à évaluer sont un échantillon. Cela signifie que, bien que le site Web existe depuis longtemps, le calcul avec VAR.S () et VARA () est basé sur les données de 18 mois (janvier 2007 à juin 2008).

Comme vous pouvez le voir à la figure , le service marketing a calculé la variance ainsi que la moyenne et la déviation moyenne.

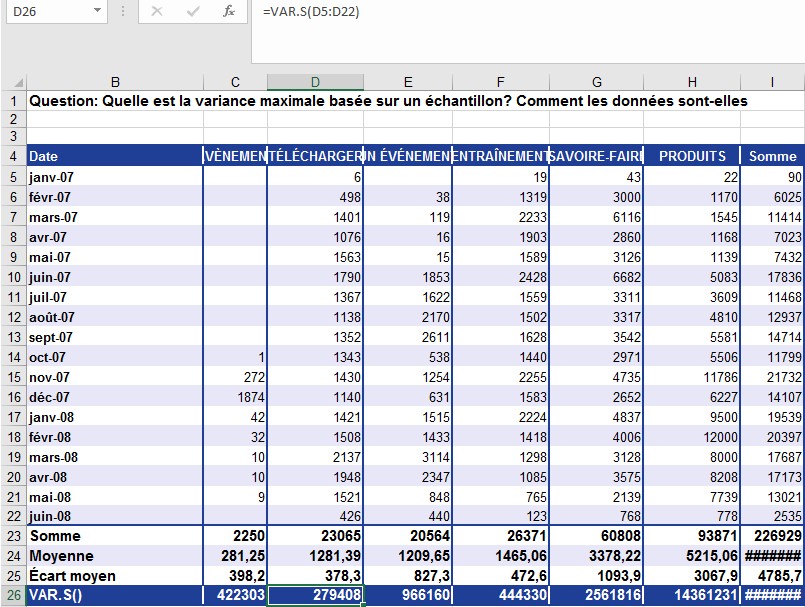
Figure . VAR.S () calcule la distribution des données autour de la moyenne en fonction d’un échantillon.

Si vous examinez de plus près la zone DOWNLOAD, vous pouvez affirmer que: L’écart au carré moyen des valeurs par rapport à la moyenne arithmétique est de 279 408 pour la zone TELECHARGER.