Supposons que quelqu’un vous dise que vous avez une taille de 19 unités. Que concluez-vous de cette information? Cela signifie-t-il que vous êtes grand? court? de hauteur moyenne? Quel pourcentage de la population est plus grand que vous?

Vous ne savez pas, et vous ne pouvez pas savoir, parce que vous ne savez pas combien vaut une “unité”. Si une unité est de 4 pouces de long, alors vous avez une taille de 76 pouces. Si une unité mesure 3 pouces de long, alors vous vous avez 57 pouces.
Le problème est qu’il n’y a rien de standard dans le mot unité. Supposons maintenant que la taille moyenne de tous les humains soit de 20 unités. Si vous avez 19 unités, vous savez que vous êtes plus petit que la moyenne.
Si, disons, 3% de la population se situe entre 19 et 20 unités, alors vous êtes seulement un peu plus petit que la moyenne. Seulement 3% de la population se situe entre vous et la taille moyenne.

Si, au contraire, 34% de la population avait entre 19 et 20 unités, vous seriez assez petit: tout le monde qui est plus grand que la moyenne de 20, plus 34% entre 19 et 20 unités, serait plus grand que vous.
Enfin, supposons que vous sachiez que la taille moyenne dans la population est de 20 unités, et que 3% de la population a entre 19 et 20 unités. Avec cette connaissance, avec le contexte fourni par la connaissance de la hauteur moyenne et de la variabilité de la hauteur, “unité” devient une norme. Maintenant, quand quelqu’un vous dit que vous avez 19 unités de taille, vous pouvez appliquer votre connaissance de la façon dont la norme se comporte, et conclure immédiatement que vous êtes un skosh plus court que la moyenne, en termes de hauteur, vous vous situez au 47ème centile.

Prendre des dispositions pour une norme
Un écart-type ressemble beaucoup à l’unité fictive décrite dans la section précédente. Dans toute distribution de fréquence qui suit une courbe normale, ces instructions sont vraies:
• Vous trouvez environ 34% des enregistrements entre la moyenne et un écart-type de la moyenne.

• Vous trouvez environ 2% des enregistrements entre deux et trois écarts-types de la moyenne. Ces normes sont affichées dans la Figure 3.4.

Figure 3.4. Ces proportions sont trouvées dans toutes les distributions normales.
 

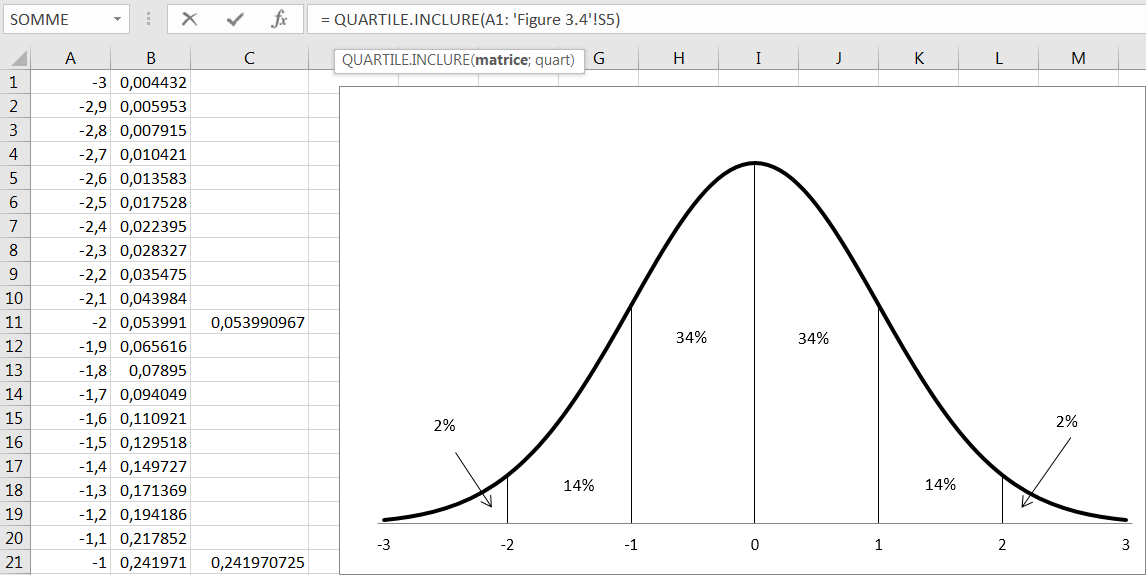
Les nombres indiqués sur l’axe horizontal de la figure 3.4 sont appelés z-scores. Un z-score, ou parfois z-value, vous indique le nombre d’écarts-types au-dessus ou en dessous de la moyenne d’un enregistrement. Si quelqu’un vous dit que votre taille en unités z-score est de +1,0, cela revient à dire que votre taille est un écart-type au-dessus de la taille moyenne.
De même, si votre poids en z-scores est de -2,0, votre poids est de deux écarts-types en dessous du poids moyen.

En raison de la façon dont les z-scores découpent la distribution de fréquence de la courbe normale, vous savez qu’un score z de +1.0 signifie que 84% des enregistrements se trouvent en dessous: Votre hauteur de 1.0 z signifie que vous êtes aussi grand que plus de 84% des autres observations. Ce 84% comprend les 50% inférieurs à la moyenne, plus les 34% entre la moyenne et un écart-type au-dessus de la moyenne. Votre poids, -2,0 z, signifie que vous ne surpassez que 2% des autres observations.
D’où le terme déviation standard. C’est la norme car peu importe que vous parliez de hauteur, de poids, de QI ou du diamètre des segments de piston. S’il s’agit d’une variable normalement distribuée, alors un écart-type supérieur à la moyenne est égal ou supérieur à 84% des autres observations. Deux écarts-types inférieurs à la moyenne sont égaux ou inférieurs à 98% des autres observations.
C’est une déviation car elle exprime une distance à la moyenne: un écart par rapport à la valeur moyenne. Et c’est à ce stade de la discussion que nous revenons au matériel du chapitre 2 concernant la moyenne, c’est-à-dire le nombre qui minimise la somme des écarts quadratiques des valeurs d’origine.

Réflexion en termes de déviations standards
À quelques exceptions près, vous risquez de penser davantage aux écarts-types qu’à d’autres mesures de la variabilité. L’écart-type est dans la même unité de mesure que la variable qui vous intéresse. Vous étudiez la distribution de miles par gallon d’essence dans un échantillon de voitures, vous pourriez constater que l’écart type est de quatre miles par gallon. Le kilométrage moyen de la marque de voiture A peut être de quatre miles par gallon, soit un écart type, supérieur au kilométrage moyen de la marque B.
C’est très pratique, et c’est une des raisons pour lesquelles les écarts-types sont si utiles. Il est utile de pouvoir penser à soi-même: «La taille moyenne est de 69 pouces. L’écart-type est de 3 pouces. La variance est une question différente. C’est le carré de l’écart-type, et c’est fondamental pour l’analyse statistique ; vous verrez beaucoup plus sur la variance dans ce chapitre et les suivants. Mais la variance ne se prête pas bien aux déclarations en anglais sur la variabilité d’une mesure telle que le cholestérol sérique ou les miles par gallon.

Par exemple, il est facile d’être à l’aise avec des affirmations telles que «Dans notre étude, la moyenne était de 20 miles par gallon et l’écart type était de 5 miles par gallon.» Vous pouvez rapidement identifier une voiture qui obtient 15 miles par gallon, un gaspilleur de gaz. Il est moins économe en carburant que 84% des autres voitures impliquées dans cette étude.
Il est beaucoup plus difficile de se sentir à l’aise avec “Dans notre étude, la moyenne était de 20 miles par gallon et la variance était de 25 miles par gallon.” Que signifie même un “mile carré par gallon”? Mais c’est ce que la variance est: le carré de l’écart-type.
Heureusement, les écarts-types sont plus intuitivement informatifs. Supposons que vous avez les miles par gallon de 10 voitures Toyota en B2: B11, et les miles par gallon de 10 voitures GM en B12: B21. Une façon d’exprimer la différence entre la consommation moyenne d’essence des deux marques est la suivante:
= (MOYENNE (B2: B11) – MOYENNE (B12: B21)) / ECARTYPE (B2: B21)
Cette formule Excel obtient la différence dans les valeurs moyennes pour les deux marques, et divise par l’écart-type des miles par gallon pour les 20 voitures. C’est illustré à la figure 3.5.
Figure 3.5. La différence entre deux marques, exprimée en unités d’écart-type.
  

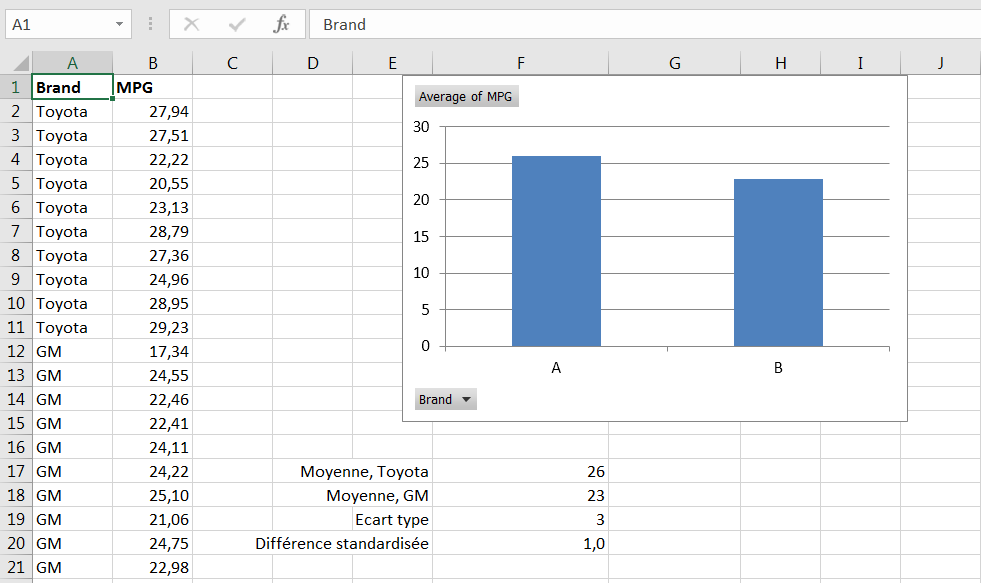
Dans la figure 3.5, la différence entre les deux marques en unités d’écart-type est de 1,0. À mesure que vous vous familiariserez avec les écarts-types, vous vous retrouverez automatiquement à penser à des choses comme «Un écart-type, c’est un peu». Exprimé de cette façon, vous n’avez pas besoin de savoir si 26 milles par gallon 23 miles par gallon est une grande différence ou un petit. Vous n’avez pas non plus besoin de savoir si 5.6 mmol / L (millimoles par litre) de cholestérol LDL est élevé, faible ou typique (voir Figure 3.6). Tout ce que vous devez savoir est que 5.6 est plus d’un écart-type au-dessus de la moyenne de 4.8 pour conclure qu’il indique un risque modéré de maladies associées à la thi le respect des parois artérielles.

Figure 3.6. La différence entre une observation et un échantillon moyen, exprimée en unités d’écart-type.

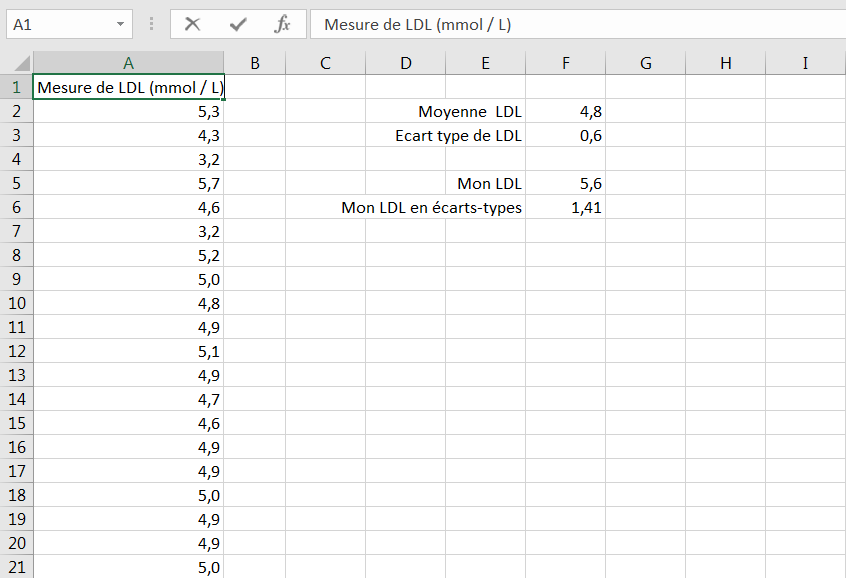
Le fait est que lorsque vous pensez en termes d’unités d’écart-type dans une distribution approximativement normale, vous savez automatiquement où se trouve un z-score dans la distribution globale. Vous savez si elle est supérieure à la moyenne (z-score positif) ou inférieure à la moyenne (z-score négatif). Vous savez à quelle distance il se trouve d’un autre z-score. Vous savez si la différence entre deux moyennes, exprimées en z, est grande ou petite.