Le test Z est un outil d’analyse statistique qui mesure la moyenne moyenne de deux grands échantillons de données lorsque l’écart type est connu. Cela ne s’applique qu’à une population qui suit une distribution normale ; Il est généralement utilisé lorsque les échantillons de données sont supérieurs à 30.

En fonction des paramètres des données, un test z peut être un test d’hypothèse à gauche, à droite ou bilatéral. Les tests Z sont similaires aux tests t, sauf que les tests t sont utilisés lorsque la taille de l’échantillon est plus petite. Le calcul de l’essai z génère un score z qui définit la position à partir de la moyenne.

Points clés à retenir

■ Le test z est utilisé pour tester des hypothèses. Lorsque la variance est fournie, elle détermine la moyenne moyenne de grands échantillons de données.

■ L’utilisation d’hypothèses nulles et alternatives permet de comparer deux populations de données, la différence entre elles et le score z.

■ Les test Z sont en outre classés en deux types. Le test sur un échantillon compare la moyenne d’un seul échantillon aux moyennes de la population. En revanche, le test à deux échantillons compare la moyenne moyenne de deux échantillons.

■ Si x̅ est la moyenne de l’échantillon, μ0 est la moyenne de la population, σ est l’écart type et n est la taille de l’échantillon, alors la formule de l’essai z est exprimée comme suit : Z = (x̅ – μ0) / (σ /√n ) . 

2 Le test Z expliqué

Le test Z est un outil statistique utilisé dans les tests d’hypothèses. C’est la méthode à privilégier lorsque la taille de l’échantillon est importante. Le test calcule la différence entre les deux grands échantillons de population, à condition que la variance soit connue. Les tests Z sont similaires aux tests t ; la seule différence est que les tests t sont effectués pour des échantillons de petite taille ou lorsque la variance est inconnue.

Encore une fois, les tests t ne sont pas effectués pour de grands ensembles de données ; d’un autre côté, les tests z ne fonctionnent pas si la taille de l’échantillon est trop petite. Il y a une limite minimale de 30 ; si la taille de l’échantillon est supérieure à 30. Ainsi, les expériences comportant moins de 30 sujets sont qualifiées de petite taille d’échantillon.

Avant d’approfondir le test, examinons rapidement les tests d’hypothèses. Les tests d’hypothèses permettent de déterminer si une hypothèse particulière est vraie pour l’ensemble de la population. C’est une application statistique. Il détermine la validité de l’inférence en évaluant des échantillons de données provenant de la population globale.

Le concept d’hypothèse fonctionne sur la probabilité d’occurrence d’un événement. Il confirme si les résultats de l’hypothèse principale sont corrects ou non. En recherche, il est très important d’éliminer le hasard. Les données ne doivent pas avoir été causées par le hasard ou par un facteur aléatoire. Les tests d’hypothèses éliminent ces incertitudes.

La définition du test z met l’accent sur une hypothèse importante : les données de l’échantillon sont une distribution normale. Autrement dit, un échantillon donné est normalement distribué ; il n’y a aucune influence d’un facteur externe.

Les tests Z sont classés en deux :

1. Un test sur échantillon compare la moyenne d’un seul échantillon aux moyennes de la population.
2. Les tests à deux échantillons comparent la moyenne moyenne de deux échantillons.

3 Formule de test Z

La formule du test z est la suivante :

Z = (x̅ – μ0) / (σ /√n)

■ Ici, x̅ est la moyenne de l’échantillon ;

■ μ0 est la moyenne de la population ;

■ σ est l’écart type ;

■ n est la taille de l’échantillon.

Sur la base du résultat du test Z, la recherche tire la conclusion de l’hypothèse. Il peut s’agir d’une valeur nulle ou d’une alternative. Ils sont mesurés à l’aide de la formule suivante :

H ₀ : μ=μ ₀

ou

H _a : μ≠μ ₀

Ici,

■ H ₀ = Hypothèse nulle

■ H _a = Hypothèse alternative

L’hypothèse nulle est vérifiée si la valeur moyenne est égale à la moyenne de la population. Dans le cas contraire, l’hypothèse alternative est prise en considération.

Un professeur affirme que tous les étudiants de première année possèdent un QI supérieur à la moyenne. Au hasard, un test a été effectué sur trente étudiants, ce qui a abouti à un QI moyen de 117. La moyenne de la population (de l’ensemble du groupe d’étudiants de première année) était de 100 et l’écart type était de 27.

Il faut identifier les hypothèses nulles et alternatives pour vérifier si l’affirmation du professeur est vraie.

■ Hypothèse nulle – H ₀ : μ = 100

■ Hypothèse alternative – H _a : μ > 100

Ensuite, on ajuste le niveau de signification. Enfin, on trouve la valeur z ou z-score. Ensuite, on met les valeurs données dans la formule z-trial :

■ Z = (x̅ – μ0) / (σ /√n)

■ Z = 117 – 100/ (27/√30)

■ Z = 17/ (27/5,477)

■ Z = 17/4,929

■ Z = 3,44

On compare maintenant le score z avec le niveau de signification.

Après avoir comparé le niveau de signification avec le score z, l’analyste accepte ou rejette l’hypothèse nulle.

Exemple

Un médecin affirme qu’un hôpital particulier accueille plus de 100 patients diabétiques avec un taux de sucre de 234 ou plus.

Pour vérifier cette affirmation, un test aléatoire a été réalisé sur 90 patients diabétiques. Le test a abouti à un taux de sucre dans le sang moyen de 279. De plus, le test a abouti à un écart type de 18.

Ici, nous avons fixé le niveau de signification à 22,50.

Les parcours Z comportent trois étapes principales :

1. Identifier les hypothèses nulles et alternatives.
2. Mesurer la signification statistique.
3. Comparaison du score z avec le niveau de signification. Sur la base de la comparaison, l’hypothèse nulle est soit acceptée, soit rejetée.

■ Ainsi, l’hypothèse nulle, H0 : µ = 234

■ L’hypothèse alternative, H _a : µ > 234

Maintenant, nous substituons les valeurs données dans la formule d’essai z :

■ Z = (x̅ – μ0) / (σ /√n)

■ Z = 279 – 234 / 18/√90

■ Z = 45 / (18/9,48)

■ Z = 45/1,89

■ Z = 23,80

Enfin, le score z (23,80) est comparé au niveau de signification.

22,50 < 23,80 ; l’affirmation du médecin s’avère exacte.

Interprétation

Le calcul du test z fournit un score z qui définit la position du score brut par rapport à la moyenne. Ceci est exprimé en unités de l’écart type.

Le score z est le nombre d’écarts types entre la valeur donnée et la moyenne. Si sa valeur est supérieure à la moyenne, alors le score z est positif, et si elle se situe en dessous de la moyenne, la valeur du score z est négative.

Les scores Z normalisent les distributions normales, ce qui permet aux analystes de mesurer la probabilité de score au sein de la distribution normale. Cela facilite la comparaison de deux scores différents provenant d’échantillons différents (avec la possibilité d’avoir des moyennes et des écarts types différents).

4 Fonction de test Excel Z

Excel Z TEST est une sorte de test d’hypothèse utilisé pour tester l’hypothèse alternative par rapport à l’hypothèse nulle. L’hypothèse nulle est une hypothèse qui fait référence à un énoncé commun en général. En effectuant un test d’hypothèse, nous pouvons essayer de prouver que l’hypothèse nulle est fausse par rapport à l’hypothèse alternative.

Par exemple, supposons que nous ayons les données (6,7,8,9,5,4,10,4) de A7 : A14. Ensuite, pour calculer la valeur de probabilité unilatérale d’un Z.TEST pour les données avec une moyenne de population hypothétique de 4, nous utiliserons la formule suivante :

=Z.TEST(A7:A14,4)

= 0,00052.

La fonction Z.TEST est l’une de ces fonctions de test d’hypothèse. Il teste la moyenne des deux ensembles de données échantillons lorsque la variance est connue et que la taille de l’échantillon est grande. La taille de l’échantillon doit être >= 30. Sinon, nous devons utiliser T-TEST. Pour Z.TEST, nous devons disposer de deux points de données indépendants qui ne sont pas liés les uns aux autres ou ne s’affectent pas les uns les autres. Nous devrions normalement distribué les données.

Syntaxe

Le Z.TEST est la fonction intégrée dans Excel. Ci-dessous la formule de la fonction Z.TEST dans Excel.

=TEST.Z(matrice;x;[sigma])

■ Matrice : Il s’agit de la plage de cellules contenant des points de données par rapport auxquels nous devons tester x . La valeur des cellules par rapport à la moyenne de l’échantillon d’hypothèse doit être testée.

■ x : A partir du tableau, la valeur x doit être testée.

■ sigma : Il s’agit de l’écart type de la population globale. C’est un argument facultatif. Si cela est omis, Excel utilise l’écart type de l’échantillon.

Comment effectuer le test Z dans Excel ? (Avec exemples)

Exemple n°1 – Utilisation de la formule Z.Test

 Regardez les données ci-dessous.

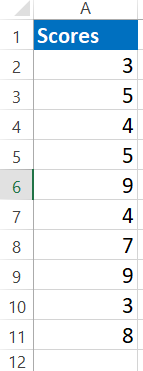
Nous utiliserons ces données pour calculer la valeur de probabilité unilatérale de Z.TEST. Pour cela, supposons l’hypothèse population signifie 6.

Les étapes pour utiliser la formule Z.Test dans Excel sont les suivantes :

1. Alors, ouvrez la formule Z.TEST dans une cellule Excel.
2. Sélectionnez le tableau sous forme de scores, A2 à A11.
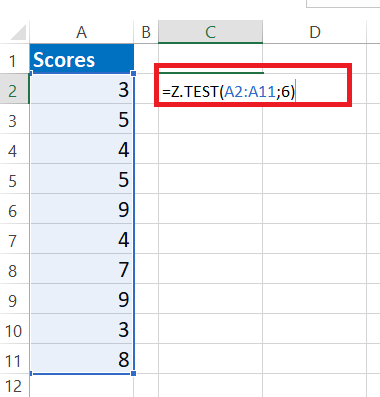
3. L’argument suivant est « x ». Puisque nous avons déjà supposé que la moyenne hypothétique de la population est de 6, appliquez cette valeur à cet argument.
4. Le dernier argument est facultatif, fermez donc la formule pour obtenir la valeur Z.TEST.

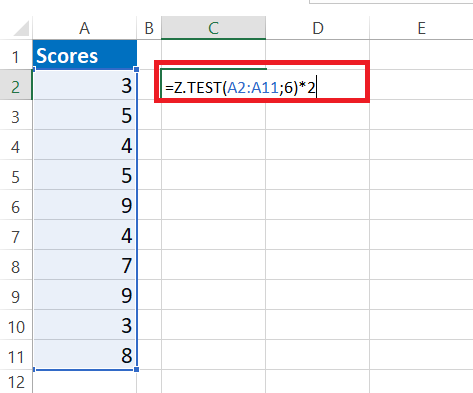
5. Il s’agit d’une valeur Z TEST unilatérale pour obtenir la valeur Z.TEST bilatérale multiplier cette valeur par 2.

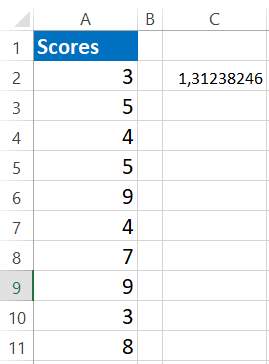
Exemple n ° 2 – TEST Z utilisant l’option d’analyse des données

Nous pouvons effectuer Z.TEST en utilisant l’option « Analyse des données » dans Excel. Pour comparer deux moyennes lorsque la variance est connue, nous utilisons Z.TEST. Nous pouvons formuler ici deux hypothèses. L’une est « l’hypothèse nulle ». Une autre est « l’hypothèse alternative » ci-dessous qui est l’équation de ces deux hypothèses.

H0 : μ1 – μ2 = 0 (hypothèse nulle)

H1 : μ1 – μ2 ≠ 0 (hypothèse alternative)

L’hypothèse alternative (H1) stipule que les moyennes des deux populations ne sont pas égales.

Nous utiliserons les résultats de deux étudiants dans plusieurs matières pour cet exemple.

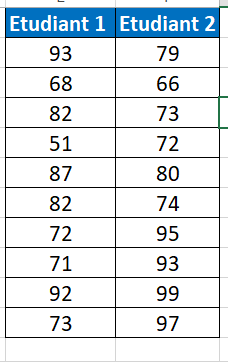
• Étape 1 :Tout d’abord, nous devons calculer les variables pour ces deux valeurs à l’aide de la fonction VAR.P.

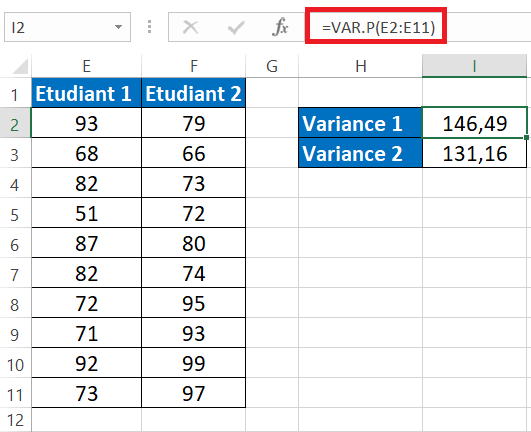
• Étape 2 :Accédez à l’onglet « Données » et cliquez sur « Analyse des données ».

Faites défiler vers le bas et sélectionnez Test z: Deux échantillons pour les moyennes » et cliquez sur « OK ».

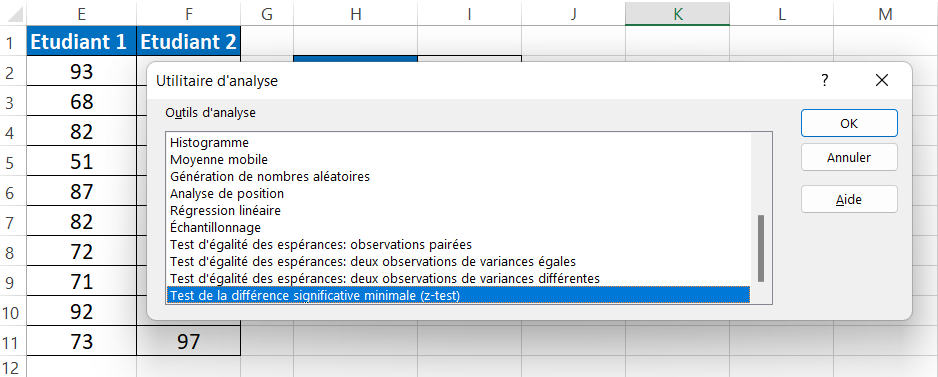
• Étape 3 :Pour la « Plage de la variable 1 », sélectionnez les scores de « Étudiant 1 ». Pour la « Plage de la variable 2 », sélectionnez les scores de « Étudiant 2 ».

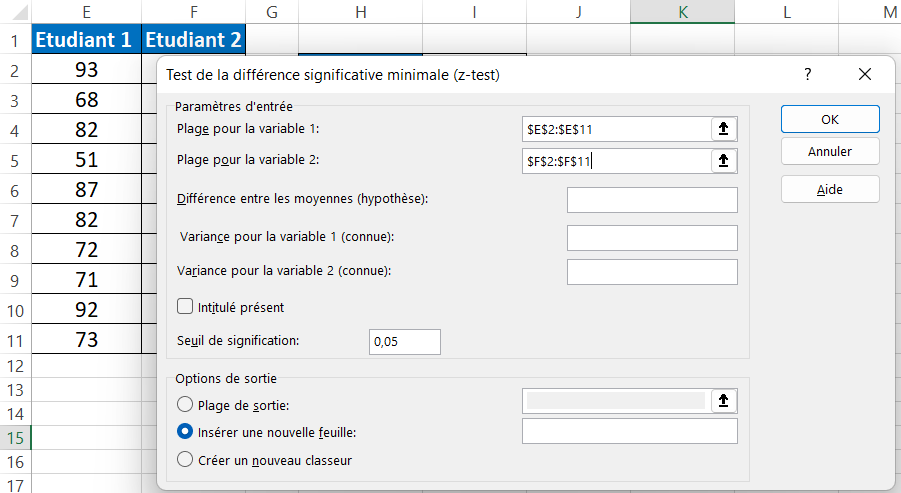
• Étape 4 :Pour « Variation de la variable 1 (connue) », sélectionnez le score de variance « Étudiant 1 » et pour « Variance de la variable 2 (connue) », sélectionnez le score de variance « Étudiant 2 ».

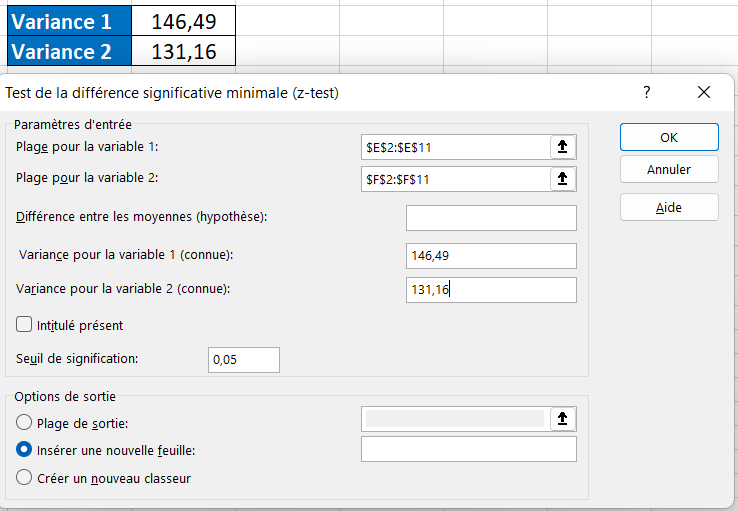
• Étape 5 :Sélectionnez la « Plage de sortie » comme cellule et appuyez sur « OK ».

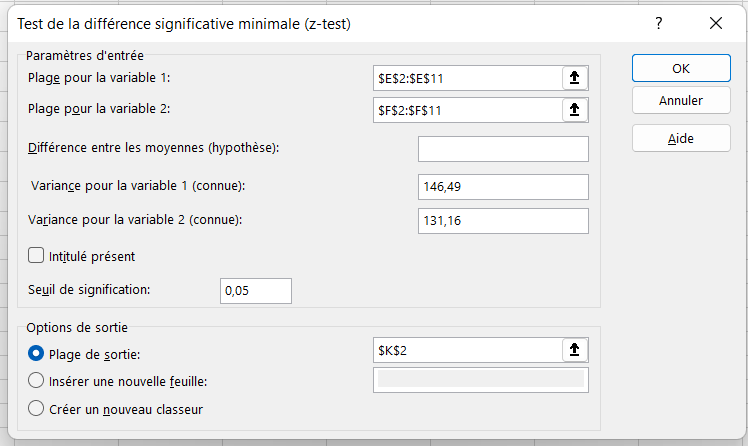
Nous avons eu le résultat.

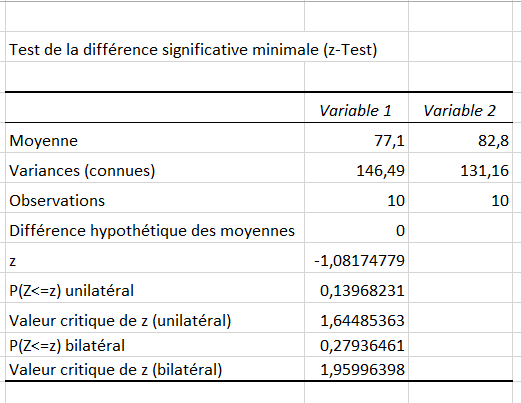
Nous pouvons rejeter l’hypothèse nulle si 

■ Z < – valeur critique de z (bilatéral)

■ Z > valeur critique de z (bilatéral).

Ainsi, à partir du résultat Z.TEST, voici les résultats.

Z < -valeur critique de z (bilatéral) = -1,080775083> – 1,959963985

Z > valeur critique de z (bilatéral) = -1,080775083 < 1,959963985

Puisqu’il répond à nos critères, nous ne pouvons pas rejeter l’hypothèse nulle. Les moyennes des deux étudiants ne diffèrent donc pas significativement.

Tous les arguments doivent être des valeurs numériques. Sinon, nous obtiendrons la #VALEUR ! Erreur. La valeur du tableau doit contenir des nombres. Sinon, nous obtiendrons une erreur #N/A.

Un test Z est donc utilisé dans les tests d’hypothèse pour déterminer si un résultat ou une association est statistiquement significatif. Il teste si deux moyennes sont identiques. De plus, on peut également l’utiliser si l’écart type de la population est connu et que la taille de l’échantillon est de 30 points de données ou plus.