Les variables aléatoires binomiales, hypergéométriques et négatives binomiales avec Microsoft Excel
■■ Qu’est-ce qu’une variable aléatoire binomiale?
■■ Comment puis-je utiliser la fonction LOI.BINOMIALE pour calculer les probabilités binomiales?
■■ Si un nombre égal de personnes préfèrent le coke à Pepsi et Pepsi à Coke et je demande à 100 personnes si elles préfèrent le coke à Pepsi, quelle est la probabilité qu’exactement 60 personnes préfèrent le coke à Pepsi et la probabilité qu’entre 40 et 60 personnes préfèrent le coke à Pepsi?
■■ De tous les rails d’ascenseur produits par mon entreprise, 3% sont considérés comme défectueux. Nous sommes sur le point d’expédier un lot de 10 000 rails d’ascenseur à un client. Pour déterminer si le lot est acceptable, le client choisira au hasard un échantillon de 100 rails et vérifiera si chaque rail échantillonné est défectueux. Si deux rails échantillonnés ou moins sont défectueux, le client acceptera le lot. Comment puis-je déterminer la probabilité d’acceptation du lot?
■■ Les compagnies aériennes n’aiment pas les vols avec des sièges vides. Supposons qu’en moyenne, 95% de tous les détenteurs de billets se présentent pour un vol. Si la compagnie aérienne vend 105 billets pour un vol de 100 places, quelle est la probabilité que le vol soit en surréservation?
■■ Le Village Deli local sait que 1 000 clients viennent déjeuner chaque jour. En moyenne, 20% commandent le sandwich végétarien de spécialité. Ces sandwichs sont préfabriqués. Combien l’épicerie devrait-elle faire si elle veut avoir 5% de chances de manquer de sandwichs végétariens?
■■ Qu’est-ce que la variable aléatoire hypergéométrique?
■■ Quelle est la variable aléatoire binomiale négative?
Qu’est-ce qu’une variable aléatoire binomiale?
Une variable aléatoire binomiale est une variable aléatoire discrète utilisée pour calculer les probabilités lorsque les trois conditions suivantes s’appliquent:
■■ n essais indépendants ont lieu.
■■ Chaque essai aboutit à l’un des deux résultats: succès ou échec.
■■ Dans chaque essai, la probabilité de succès (p) reste constante.
Dans une telle situation, la variable aléatoire binomiale peut être utilisée pour calculer les probabilités liées au nombre de succès dans un nombre donné d’essais. Soit x la variable aléatoire indiquant le nombre de succès survenus dans n essais indépendants lorsque la probabilité de succès sur chaque essai est de p. Voici quelques exemples dans lesquels la variable aléatoire binomiale est pertinente:
■■ Coke ou Pepsi Supposons qu’un nombre égal de personnes préfèrent le Coke au Pepsi et le Pepsi au Coke. Vous demandez à 100 personnes si elles préfèrent le Coca-Cola à Pepsi. Vous êtes intéressé par la probabilité qu’exactement 60 personnes préfèrent le Coca-Cola à Pepsi et la probabilité que de 40 à
60 personnes préfèrent Coca-Cola à Pepsi. Dans cette situation, vous avez une variable aléatoire binomiale définie
par ce qui suit:
- • Essai: enquête auprès des individus
- • Succès: préférez le coke
- • p est égal à 0,50
- • n est égal à 100
Soit x égal au nombre de personnes échantillonnées qui préfèrent le coke. Vous voulez déterminer la probabilité que x = 60 et 40 ≤ x ≤ 60.
■■ Rails d’ascenseur De tous les rails d’ascenseur que vous produisez, 3% sont considérés comme défectueux.
Vous êtes sur le point d’expédier un lot de 10 000 rails d’ascenseur à un client. Pour déterminer si le lot est acceptable, le client choisira au hasard un échantillon de 100 rails et vérifiera si chaque rail échantillonné est défectueux. Si deux rails échantillonnés ou moins sont défectueux, le client accepte le lot. Vous souhaitez déterminer la probabilité d’acceptation du lot.
Vous avez une variable aléatoire binomiale définie par ce qui suit:
- • Essai: regardez un rail échantillonné
- • Succès: le rail est défectueux
- • p est égal à 0,03
- • n est égal à 100
Soit x égal au nombre de rails défectueux dans l’échantillon. Vous voulez trouver la probabilité que
x ≤ 2.
■■ Surbooking des compagnies aériennes Les compagnies aériennes n’aiment pas les vols avec des sièges vides. Supposons qu’en moyenne,
95 pour cent de tous les détenteurs de billets se présentent pour un vol. Si la compagnie aérienne vend 105 billets pour un vol de 100 places, quelle est la probabilité que le vol soit en surréservation?
Vous avez une variable aléatoire binomiale définie par ce qui suit:
- • Essai: détenteurs de billets individuels
- • Succès: le détenteur du billet se présente
- • p est égal à 0,95
- • n est égal à 105
Soit x égal au nombre de détenteurs de billets qui se présentent. Ensuite, vous voulez trouver la probabilité
que x ≥ 101.
Comment puis-je utiliser la fonction BINOM.DIST pour calculer les probabilités binomiales?
Microsoft Excel inclut la fonction LOI.BINOMIALE, que vous pouvez utiliser pour calculer les probabilités binomiales. Si vous souhaitez calculer la probabilité de succès x ou moins pour une variable aléatoire binomiale ayant n essais avec probabilité de succès p, entrez simplement BINOM.DIST (x, n, p, 1). Si vous souhaitez calculer la probabilité d’exactement x succès pour une variable aléatoire binomiale ayant n essais avec une probabilité de réussite de p, entrez LOI.BINOMIALE (x, n, p, 0). Entrer 1 comme dernier argument de LOI.BINOMIALE donne une probabilité cumulative; entrer 0 donne t La fonction de masse de probabilité pour une valeur particulière. (Notez qu’un dernier argument de True peut être utilisé au lieu d’un 1, et un dernier argument de False peut être utilisé au lieu d’un 0.) Les versions précédentes d’Excel ne reconnaîtront pas la fonction LOI.BINOMIALE. Dans les versions précédentes d’Excel, vous pouvez utiliser la fonction BINOMDIST, qui a exactement la même syntaxe que la fonction LOI.BINOMIALE. Utilisons la fonction BINOM.DIST pour calculer certaines probabilités d’intérêt. Vous trouverez les données et l’analyse dans le fichier Binomialexamples.xlsx, illustré à la figure 1.
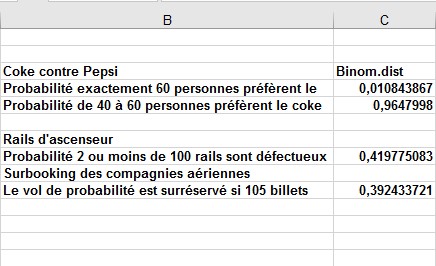
FIGURE 1 Utilisation de la variable aléatoire binomiale.
Si un nombre égal de personnes préfèrent le coke à Pepsi et Pepsi à Coke et je demande à 100 personnes si elles préfèrent le coke à Pepsi, quelle est la probabilité qu’exactement 60 personnes préfèrent le coke à Pepsi et la probabilité qu’entre 4 et 60 personnes préfèrent le coke à Pepsi ?
Vous avez n = 100 et p = 0,5. Vous recherchez la probabilité que x = 60 et la probabilité que 40 ≤ x ≤ 60, où x est égal au nombre de personnes qui préfèrent le Coca-Cola au Pepsi. Tout d’abord, vous trouvez la probabilité que x = 60 en entrant la formule BINOM.DIST (60,100,0.5,0). Excel renvoie la valeur 0,011.
Pour utiliser la fonction LOI.BINOMIALE pour calculer la probabilité que 40 ≤ x ≤ 60, vous pouvez noter que la probabilité que 40 ≤ x ≤ 60 est égale à la probabilité que x ≤ 60 moins la probabilité que x ≤ 39. Ainsi, vous pouvez obtenir la probabilité que de 40 à 60 personnes préfèrent le coke en entrant la formule LOI.BINOMIALE (60,100,0,5,1) –LOI.BINOMIALE (39,100,0,5,1). Excel renvoie la valeur 0,9648. Donc, si le Coke et le Pepsi sont également préférés, il est très peu probable que dans un échantillon de 100 personnes, le Coke ou le Pepsi soit en avance de plus de 10%. Si un échantillon de 100 personnes montre que le Coke ou le Pepsi ont plus de 10% d’avance, vous devriez probablement douter que le Coke et le Pepsi soient également préférés.
De tous les rails d’ascenseur produits par mon entreprise, 3% sont considérés comme défectueux. Nous sommes sur le point d’expédier un lot de 10 000 rails d’ascenseur à un client. Pour déterminer si le lot est acceptable, le client choisira au hasard un échantillon de 100 rails et vérifiera si chaque rail échantillonné est défectueux. Si deux rails échantillonnés ou moins sont défectueux, le client acceptera le lot. Comment puis-je déterminer la probabilité d’acceptation du lot?
Si vous laissez x égal au nombre de rails défectueux dans un lot, vous avez une variable aléatoire binomiale avec n = 100 et p = 0,03. Vous recherchez la probabilité que x ≤ 2. Entrez simplement LOI.BINOMIALE (2,100,0.03,1) formule dans la cellule C8. Excel renvoie la valeur 0,42. Ainsi, le lot sera accepté 42% du temps.
Vraiment, vos chances de succès ne sont pas exactement de 3% à chaque essai. Par exemple, si les 10 premiers rails sont défectueux, la probabilité que le prochain rail soit défectueux est tombée à 290/9 990; si les 10 premiers rails ne sont pas défectueux, la probabilité que le prochain rail soit défectueux est de 300/9 990. Par conséquent, la probabilité de succès sur le onzième essai n’est pas indépendant de la probabilité de succès d’un des dix premiers essais. Malgré ce fait, la variable aléatoire binomiale peut être utilisée comme approximation lorsqu’un échantillon est tiré et que la taille de l’échantillon est inférieure à 10% de la population totale. Ici, la population est égale à 10 000 et la taille de l’échantillon est de 100. Les probabilités exactes impliquant l’échantillonnage d’une population finie peuvent être calculées avec la variable aléatoire hypergéométrique, qui est discutée plus loin dans cet article.
Les compagnies aériennes n’aiment pas les vols avec des sièges vides. Supposons qu’en moyenne, 95% de tous les détenteurs de billets se présentent pour un vol. Si la compagnie aérienne vend 105 billets pour un vol de 100 places, quelle est la probabilité que le vol soit en surréservation?
Soit x le nombre de détenteurs de billets qui se présentent pour le vol. Vous avez n = 105 et p = 0,95. Vous recherchez la probabilité que x ≥ 101. Notez que la probabilité que x ≤ 101 soit égal à 1 moins la probabilité que x ≤ 100. Donc, pour calculer la probabilité que le vol soit surréservé, vous entrez 1 – LOI.BINOMIALE(100,105,0,95,1) formule dans la cellule C10. Excel donne 0,392, ce qui signifie qu’il y a un 39,2 pourcent de chances que le vol soit surbooké.
Le Village Deli local sait que 1 000 clients viennent déjeuner chaque jour. En moyenne, 20% commandent le sandwich végétarien de spécialité. Ces sandwichs sont préfabriqués. Combien l’épicerie devrait-elle faire si elle veut avoir 5% de chances de manquer de sandwichs végétariens?
Dans Excel , la fonction LOI.BINOMIALE.INV, avec la syntaxe LOI.BINOMIALE.INV (essais, probabilité de succès, alpha), détermine le plus petit nombre x pour lequel la probabilité de réussite inférieure ou égale à x est au moins alpha. Dans les versions antérieures d’Excel, la fonction CRITERE.LOI.BINOMIALE(essais, probabilité de succès, alpha) a donné les mêmes résultats que LOI.BINOMIALE.INV. Dans cet exemple, les essais sont égaux à 1 000, la probabilité de succès est égale à 0,2 et l’alpha est égal à 0,95. Comme le montre la figure 2, si la charcuterie commande 221 sandwichs, la probabilité que la demande soit inférieure ou égale à 221 est d’au moins 0,95. UNE Aussi, la probabilité que 220 sandwichs ou moins soient demandés est inférieure à 0,95.
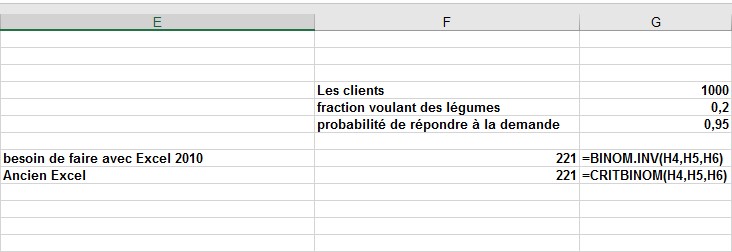
FIGURE 2 Exemple de fonction LOI.BINOMIALE.INV.
Qu’est-ce que la variable aléatoire hypergéométrique?
La variable aléatoire hypergéométrique régit une situation telle que la suivante:
■■ Une urne contient N balles.
■■ Chaque balle est de deux types (appelée succès ou échec).
■■ Il y a des succès dans l’urne.
■■ Un échantillon de taille n est tiré de l’urne.
Regardez un exemple dans le fichier Hypergeom.dist.xlsx, qui est illustré à la figure 3. Excel 2013
LOI.HYPERGEOMETRIQUE.N (x, n, s, N, 0) formule la probabilité de x succès si n balles sont tirées d’une urne contenant N balles, dont s sont marquées comme succès. La formule Excel 2013 (x, n, s, N, 1) donne une probabilité inférieure ou égale à x succès si n balles sont tirées d’une urne contenant N balles, dont s sont marquées comme succès . (Comme pour la fonction Loi.BINOMIALE, VRAI peut être utilisé pour remplacer 1 et False pour remplacer 0.)
Par exemple, supposons que 40 des sociétés du Fortune 500 aient une femme PDG. Les 500 PDG sont analogues aux balles dans l’urne (N = 500), et les 40 femmes sont représentatives des succès de l’urne. Ensuite, la copie de la formule HYPERGEOM.DIST (C8, Sample_size, Population_women, Population_size, 0) de D8 à D9: D18 donne la probabilité qu’un échantillon de 10 entreprises Fortune 500 avoir 0, 1, 2,. . . , 10 femmes PDG. Ici, Sample_size est égal à 10, Population_women est égal à 40 et Population_taille est égal à 500.
Trouver une femme PDG est un succès. Dans l’échantillon de 10, par exemple, il y a une probabilité de 0,431 qu’aucune femme PDG ne fasse partie de l’échantillon. Soit dit en passant, vous auriez pu approximer cette probabilité avec la formule LOI.BINOMIALE (0,10,0.08,0), donnant 0,434, ce qui est très proche de la vraie probabilité de 0,431. Dans la cellule F10, la probabilité qu’au plus 2 des 10 personnes de l’échantillon soient des femmes était calculé avec la formule LOI.HYPERGEOMETRIQUE.N (2, meme taille, Population de femme, Population_taille, Vrai). Ainsi, il y a 96,2% de chances qu’au plus deux personnes de l’échantillon soient des femmes. Bien sûr, vous auriez pu obtenir cette réponse en ajoutant les cellules ombrées (D8: D10) ensemble.
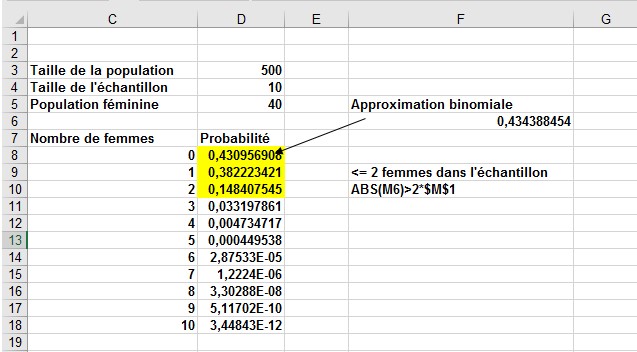
FIGURE 3 Utilisation de la variable aléatoire hypergéométrique.
Quelle est la variable aléatoire binomiale négative?
La variable aléatoire binomiale négative s’applique à la même situation que la variable aléatoire binomiale, mais la variable aléatoire binomiale négative donne la probabilité de f échecs se produisant avant la réussite de sth. Ainsi, = LOI.BINOMIALE.NEG.
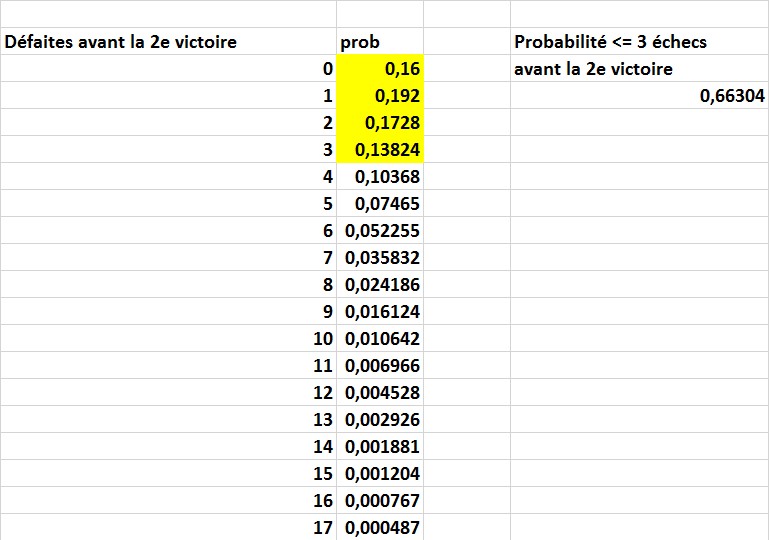
FIGURE 4 Utilisation de la variable aléatoire binomiale négative.
